Índice Hearst - página 45

Novo comentário
 

A versão R 3.0.0 já está disponível.

Tudo tem que ser reinstalado, inclusive o RStudio.

A propósito, alguém sabe como se livrar das 4 janelas obrigatórias.

 

faa1947:  

A propósito, alguém sabe como se livrar das 4 janelas obrigatórias.

Ao arrastar as bordas verticais e horizontais, você pode esconder as janelas de que não precisa.
 
WWer:
Ao arrastar as bordas verticais e horizontais, você pode esconder janelas que não precisa.
De fato, obrigado.
 

A propósito, se alguém estiver interessado:

Puxe Renko na tabela até exatamente o primeiro joelho do Ziguezague de e para a palheta.

E no joelho zero, veja o atraso ou avanço do início da Renko em relação ao pico do Ziguezague.

O sistema é montado como uma fibra, mas o resultado é uma curva no subsolo a partir do nível zero.

 

Não faz muito tempo que o destino me colocou em contato com este tópico e várias perguntas surgiram imediatamente. Caros especialistas, vocês poderiam me ajudar a encontrar respostas a estas perguntas? Não me chute se alguma das perguntas lhe parecer idiota...

Portanto:

1) Há várias maneiras de encontrar o índice Hurst. Qual destas formas (na sua opinião) é a melhor (dá uma estimativa mais precisa do índice)? Se possível, forneça um link para a fonte.

2) O indicador deve ser invariante sob transformações lineares? (Uma resposta detalhada é desejável).

3) Se as séries estão correlacionadas umas com as outras, o que pode ser dito sobre o índice Hurst?

4) Existem três séries. Um índice Hurst é calculado para cada série. Quando as séries são somadas, o que pode ser dito sobre o expoente?

Agradeço antecipadamente.

 

Devemos iniciar uma linha separada sobre o uso da linguagem R? Compartilhar experiências e resultados.

É claro, se alguém estiver interessado.

Boa sorte.

 

Voltei novamente à análise deste indicador não trivial. Durante muito tempo fiquei confuso com o coeficiente lateral obtido pelo cálculo do valor do Hearst. Essencialmente, Hearst é uma equação linear em dupla escala logarítmica, onde no eixo de ordenadas (Y) é dada a distância percorrida pelo preço na escala ajustada, e no eixo de abcissas (X) - um período específico (período de tempo ou horizonte). Esta equação linear é uma aproximação dos pontos que experimentalmente medimos e plotamos. A fórmula para a equação é simples e óbvia:

Vamos fingir por um tempo que o coeficiente é zero e simplificar a fórmula para 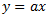. O valor 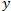aqui é a distância percorrida pelo preço. O valor 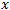é o período de tempo. Obviamente, em um movimento Browniano clássico o preço percorre uma distância correspondente à raiz quadrada de , onde 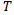é o tempo ou o período:

Esta equação é um caso especial de nossa fórmula, em :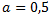

Esta fórmula em dupla escala logarítmica corresponderá à nossa função linear propriamente dita:

Onde 0,5 é o coeficiente de Hurst.

Todos estes cálculos são triviais, mas negligenciam o coeficiente incômodo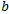 , que na realidade é quase sempre um número significativo. Então, como entendemos este coeficiente? Minhas reflexões matemáticas sobre a natureza desta dependência levaram a uma compreensão deste coeficiente. Afinal, ela só aparece quando nos aproximamos de nossos pontos empíricos por uma função linear. Para cada ponto em particular, seu H é sempre conhecido. Ele não tem o coeficiente porque também não há uma função aproximada geral para ele. Vamos considerar um exemplo simples, vamos tentar calcular H visualmente para os pontos C e D R/S do gráfico EURUSD:

Para o ponto C é aproximadamente 0,45, para o ponto D é 0,51. Como ambos os pontos se encontram quase perfeitamente na linha aproximada(y = 0,5304x - 0,0757 ) podemos calcular analiticamente os valores exatos de H para estes pontos. Para C:

Para D:


Ao realizar a transformação inversa para D, para este ponto o valor Y é 1,5155 e o valor X corresponde a 3, então seu H será:

O resultado do cálculo mostra que o ponto C é antipersistente (H = 0,4547) e D é na verdade Brownian (H = 0,5051). A estimativa de H para toda a série se torna sem sentido, porque em um horizonte pequeno a série é anti-tendência, enquanto em um horizonte maior tende a se tornar mais trendy. Isto é totalmente consistente com as observações empíricas sobre moedas. Todos que os comercializam por tempo suficiente vêem que em escalas pequenas os preços flutuam constantemente no plano, e em escalas maiores, durando um ano ou mais, há grandes movimentos de tendência.

O coeficiente é uma espécie de correção relativista em física. Ela forma uma correlação com H e determina a mudança do caráter do mercado com o aumento da escala. Se este coeficiente é próximo de zero, o mercado é homogêneo em sua escala. A tendência ou antipessoalidade nele está aproximadamente no mesmo nível, independentemente da escala. Se b é significativo - é a condição inicial dominante. H - começa a dominar mais com o aumento da escala. Aqui estão os tipos de relacionamento entre H e:

  • H é maior que 0,5; b é um número negativo. Com esta combinação, o mercado é anti-tendência em pequena escala, mas à medida que o prazo aumenta, as tendências começam a aparecer. Este comportamento é exibido por moedas;
  • H é maior que 0,5; b é um número positivo. O mercado é homogêneo. As tendências dominam em todas as escalas de tempo. Se H é significativo e b não é significativo, as tendências mais fortes são mais frequentemente vistas em horizontes temporais maiores. Quanto mais longo o horizonte, mais fortes são as tendências. Pelo contrário, se H não é considerável e b é grande - tendências mais fortes podem ser encontradas em escalas de tempo pequenas, e à medida que o período cresce, as tendências continuam a aparecer, mas sua força e pureza diminuem.
  • H é inferior a 0,5; b é um número negativo. O mercado é antipessoal em todas as escalas. Se H é significativo e b não é - retornos mais frequentes e mais limpos à média ocorrem em prazos maiores. Em prazos menores, o preço é mais propenso a vaguear ao acaso. Se, pelo contrário, b é significativo e H não é - o mercado é mais propenso a voltar em pequenos períodos de tempo, em períodos mais longos o mercado está mais próximo de um movimento browniano, mas ainda mantém sua antipessoalidade.
  • H é inferior a 0,5; b é um número positivo. Com esta combinação, o mercado está tendendo em pequenas escalas, mas se torna anti-tendência em mastros maiores. Aparentemente, tal comportamento foi observado no período de preço do petróleo na região de 100 dólares por barril.

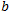Se b modulo é uma fração significativa de H, então você não pode limitar sua análise ao H. O mercado pode exibir duas propriedades opostas em diferentes escalas de tempo, por exemplo, ter tendência e contra-tendência ao mesmo tempo.

Se H e b são significativos e apontam em direções diferentes (H é significativamente maior que 0,5 e é negativo ou H é significativamente menor que 0,5 e b é positivo) - o mercado mostra mudanças bruscas de um estado para outro dependendo do período de tempo.

 

Alguém implementou a fórmula do indicador de tempo mostrada aqui:

http://cdn.scipeople.com/materials/2667/%D0%9F%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5%20RS%20%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0%20%D0%BD%D0%B0%20%D1%84%D0%BE%D0%BD%D0%B4%D0%BE%D0%B2%D1%8B%D1%85%20%D1%80%D1%8B%D0%BD%D0%BA%D0%B0%D1%85%202.doc

5 países

 
Existe um indicador Hearst para o MT4?
 
A propósito, existe um indicador chamado índice de invariância. Ele analisa a inclinação da linha de regressão, respondendo assim à pergunta se existe ou não uma tendência no mercado. Ainda não tenho tempo para usá-lo, mas quero que este índice calcule não o movimento de preços no mercado, mas o movimento da curva de equilíbrio. Isso permitiria ver se há ou não uma mudança de equilíbrio. Determinamos a direção, se está subindo, espelhamos os sinais, se está subindo, repetimos. Parece-me que qualquer sistema pode ser puxado pelos ouvidos com um ajudante assim .... Acho que qualquer TS pode ser arrancado pelos ouvidos com um ajudante assim. O que você acha?
Arquivos anexados:
ivar.mq4  4 kb
1...383940414243444546
Novo comentário