Aprendizado de máquina no trading: teoria, prática, negociação e não só - página 436
Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Está a funcionar, obrigado! Interessante como funciona...
Procura 1 opção mais parecida ou tem uma média superior a várias? Aparentemente, encontra 1 melhor. Acho que devo procurar 10 ou mesmo 100 variantes e procurar a previsão média (o número exacto deve ser determinado pelo optimizador).
Sim, aqui mostra 1 melhor, não se incomodou com muitas variantes, você pode tentar refazer se você entender minha escrita )
Nunca fui capaz de aprender a negociar com lucro usando apenas preços. Mas o modelo padrão fez, por isso a escolha é óbvia :)
Uma coisa é encontrar um "padrão", mas outra coisa é dar-lhe uma vantagem estatística. IMHO duvido muito, por alguma razão. Na verdade a busca de padrões por convolução (produto, diferença) ao longo de toda a extensão de uma série histórica com média é como fazer uma regressão em NS com UM NEURON, que é o modelo linear mais simples com sinais extremamente estúpidos, uma fatia do preço como está.
Uma coisa é encontrar um "padrão", mas outra coisa é encontrar uma vantagem estatística. IMHO, duvido muito. Na verdade a busca de padrões por convolução (produto, diferença) em toda a extensão da série histórica com média, é como fazer regressão em NS com UM NEURON, que é o modelo linear mais simples, com características extremamente burras, uma fatia do preço como está.
Se for um único neurônio, então com um número de entradas igual ao comprimento do padrão, (padrão de 30 barras = 30 entradas NSb de 500 barras = 500 entradas NS).
Para mim, muitos neurônios em camadas internas do NS são análogos à memória, 10 - 50 - 100 neurônios adicionais são correspondentemente 10 - 50 - 100 variantes memorizadas de sinais de entrada. E comparando o padrão com 375000 variantes da história (M1 durante um ano) temos uma memória absolutamente precisa e completa, em vez de 10 -50 - 100 variantes mais frequentemente encontradas. Então, a partir desta memória, o localizador de padrões identifica N resultados mais similares e obtém a previsão média, enquanto a rede neural aumenta o peso das conexões entre neurônios com todos os padrões similares.
Não está claro por que razão a convolução deve ser aplicada, presumo que se propõe convolver o padrão procurado com cada variante da história, como resultado obtemos a 3ª sequência temporal - e como é que isso ajuda a determinar a semelhança do padrão e da variante a ser verificada?Se for um neurônio, então com o número de entradas igual ao comprimento do modelo, (modelo de 30 barras = 30 entradas NS de 500 barras = 500 entradas NS).
Outra coisa que não está clara é por que a convolução deve ser aplicada, presumo que você se propõe a convolver o padrão pesquisado com cada variante da história, como resultado obtemos a 3ª seqüência temporal - e como ela ajuda a definir a similaridade do padrão e da variante verificada?
Sim, mostra 1 melhor aqui, não se incomodou com muitas variantes, você pode tentar refazê-lo se você entender minha escrita )
enquanto se olha para a fotografia, algo não está bem...
Aqui está um exemplo aleatório
A sua linha de previsão azul vai muito para baixo, com um movimento fraco de uma variante semelhante...
Aqui só se fotografou esta variante e a ideia não foi tão íngreme e mais lógica.
enquanto estou a olhar para a fotografia, algo não está bem...
Aqui está um exemplo aleatório
A sua linha de previsão azul desce muito acentuadamente, com um movimento fraco de uma variante semelhante...
Aqui só se fotografou esta variante e a ideia não foi tão íngreme e mais lógica.
Percebido :) em certas situações não conta o ângulo corretamente por alguma razão, começou quando eu o reescrevi de uma versão de um único período de tempo para uma versão de múltiplos períodos de tempo, e ainda não descobri onde está a falha
A propósito, é possível que eu não o tenha contado correctamente... Não pensei em verificar isso com o photoshop. O ângulo entre os gráficos anteriores e as previsões deve ser o mesmo
Exactamente.
Você colapsa o padrão e a fila onde os extremos eram mais parecidos, é simples. Por exemplo, você tem uma linha {0,0,0,0,1,2,3,1,1,1} e você quer encontrar um padrão {1,2,3} nele, a convolução lhe dará {0,0,0,0,3,8,14,11,8, 6} (contado a olho) 14 no máximo onde está a "cabeça" do nosso padrão. É claro que é desejável normalizar os vetores antes da convolução, caso contrário haverá extrema em lugares com grandes números.
Porquê complicar coisas como esta? Por que devemos procurar um extremo na convolução se podemos procurar {0,0,0,0,1,2,3,1,1,1} especificamente na linha {1,2,3}? Além de aumentar a complexidade e o tempo de computação, não vejo nenhuma vantagem.
Porquê complicar coisas como essa? Por que devemos procurar um extremo na convolução se podemos procurar {0,0,0,0,1,2,3,1,1,1} especificamente na série {1,2,3}? Além da complicação e do tempo de computação mais longo, não vejo nenhuma vantagem.
Hmmm... o que queres dizer com "procurar especificamente"? Por favor, me dê um exemplo de algoritmo mais rápido que a convolução.
Duas operações podem ser usadas: comprimento da diferença vetorial e produto escalar, comprimento da diferença, acredite-me é 3-10 vezes mais lento, diferença de componentes, quadrado, soma, extração da raiz, e convolução é multiplicar e adicionar.
Você precisa pegar cada pedaço de uma linha de comprimento 3 como um vetor e compará-lo para "similaridade" com o nosso {1,2,3}.
Hmmm... o que queres dizer com "procurar especificamente"? Por favor, me dê um exemplo de um algoritmo mais rápido que a convolução.
O mais fácil é deslocar passo a passo a largura da janela do exemplo procurado ao longo da sequência e encontrar a soma dos valores dos abs. dos deltas:
0,0,0 e 1,2,3 erro = (1-0)+(2-0)+(3-0)=6
0,0,1 e 1,2,3 erro = (1-0)+(2-0)+(3-1)=5
0,1,2 e 1,2,3 erro = (1-0)+(2-1)+(3-2)=3
1,2,3 e 1,2,3 erro = (1-1)+(2-2)+(3-3)=0
2,3,1 e 1,2,3 erro = (2-1)+(3-2)+Abs(1-3) =4
Onde o erro mínimo é a máxima semelhança.
Notado :) em certas situações, por alguma razão não conta o ângulo corretamente, ele começou depois que eu reescrevi de uma versão com um único período de tempo para a versão com vários períodos de tempo, e nunca peguei onde o bug está
A propósito, é possível que eu estivesse contando incorretamente... Eu não consegui verificar isso com o Photoshop. Devo obter o mesmo ângulo entre os gráficos e as previsões anteriores.
Ainda não tenho a certeza, que é correcto considerar os gráficos como semelhantes com uma diferença tão grande nos ângulos de inclinação. Usando o mesmo exemplo:
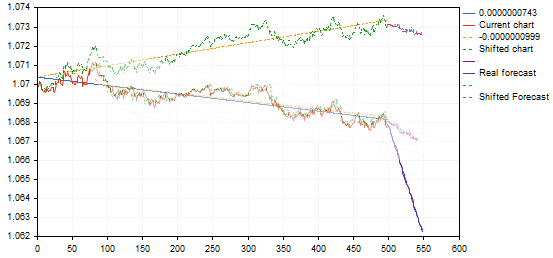
a variante encontrada dá uma recuo a partir do ponto de tendência superior ou do fim da tendência, transferindo-a para o gráfico padrão dará uma previsão para a continuação da tendência decrescente e não uma inversão - essencialmente um sinal inverso. Algo não está bem aqui.... talvez não precisemos destas transformações afins....? E a simples correlação (erro mínimo) é suficiente?