私たちのマーシャ! - ページ 2 123456789...21 新しいコメント Леонид 2009.01.19 14:31 #11 また、スムージングのレベルが高いと、収益性の向上という良い結果にはなりません。滑らかさを増すと、いずれにせよレイテンシーが増加することになる。しかし、仮に遅延がゼロであったとしても、滑らかさが増すと、小さな取引をスキップすることになり、取引量が減り、それぞれ利益が減り、その結果ドローダウンが増える......ということになるのです。 チャート上でも、理論上は取れるはずのかなり大きな取引の一部が取れず、利益が減っているのがよくわかる......。 削除済み 2009.01.19 14:44 #12 LeoV >> : また、スムージングのレベルが高いと、収益性の向上という良い結果にはなりません。滑らかさを増すと、いずれにせよレイテンシーが増加することになる。しかし,仮に遅延がゼロだと仮定しても,スムージングが進むと,より小さなトレードをスキップすることになり,その結果,トレードが減少し,それぞれ利益の減少,ドローダウンの増加につながる......ということになる。 最適なバリエーションに適応させる。 >> おっしゃるようなケースは、時間依存の指標ではすべて問題です。古典的な意味での時間をなくし、他の方法を使う。 Леонид 2009.01.19 14:45 #13 mql4com писал(а)>> 古典的な意味でのタイミングをあきらめ、他の方法を用いる。 私はとっくにこのようなTCはやめて他の方法を使っています・・・ただ、滑らかさを増すとどうなるかという意見として書き込みました ))))。 削除済み 2009.01.19 14:49 #14 LeoV писал(а)>> 私はとっくにこのようなTCは諦めて他の方法を使っています・・・ただ、滑らかさを増すとどうなるかという意見として書き込みをしました ))))) 手紙を書いてもいいですか? Леонид 2009.01.19 15:19 #15 LeoV писал(а)>> 滑らかさを増すと、より小さな動きが省略されることになり、それぞれ取引回数の減少、利益の減少、結果としてドローダウンの増加につながる......というものです。 さらに、このすべてに、遅延の増加によるエラー(損失)を追加する必要があり(利他的になる必要はありません)、利益の問題は空中でハングアップすることができます......)))) Swetten wrote(a)>> 手紙を書いてもいいですか?)))もちろん可能なのですが...。誰も個人をキャンセルしていない・・・・・・)))) Neutron 2009.01.19 16:13 #16 MVVは(a)>>を 書きました。 アイデアのオーサーシップについては議論してもいいと思う。おそらく、そのアイデアはMAと同じくらい古いものでしょう。:)) そして、一般的にこのテーマは私にとって興味深いものであり、私自身もそれに携わっています。当然ながら、すべてが絵のように美しいわけではありません。明らかに矢継ぎ早に足りない。 では、順番に。 実際には、MAの変曲点がオープン/リバーサルのシグナルとなるはずです。微分がゼロに等しいと「棚上げ」になり、その後、MAは同じ方向に動く可能性があります。 ポイント1の主な要件は、ポイント2と常に矛盾することになります。 МАを理想に近づけるためには、アダプティブであることが必要です。 私の考えでは、このようなシステムは、積極的なMMなしでは利益を得られないと思います。 さて、同志よ!- だから、正しい道を歩んでいるのです。 図は、ポジションの開閉方法を非常に模式的に示したものである。 議論の余地がある(2次導関数が0に等しい)ので、そちらからの反論が必要です。極限(一次導関数のゼロへの等化)については、議論の必要はなさそうです。 MAが引用に近いという要求と、同時に滑らかであるという要求は、相反するものではなく、互いに補完し合うものです(できない)。顕著な例として、通常の指数平均型EMAがあります。その再帰的な形式は、近接性と平滑性を同時に要求する汎関数の最小化から正確に得られる。 3.これは、メソッドの発展形と見ることができる。まず始めに、函数の形式に関する明白な要件について解答を得る必要がある。 Swetten さんが書き込みました>>1 失礼ですが、FZとは何でしょうか? FZ - 位相差。DSPからの用語です。 TheXpert 2009年01月19日 14:45 対象機能は、アウトラインの参照に基づくものですか? いいえ、私の提案したマヴの要件とあなたの修正を基に、ターゲット機能を構築する必要があります。 LeoV さんが書き込みました(・a・) >>。 あまりにスムージングをしすぎると、良い結果が得られない。つまり、利益が増えてしまう。滑らかさを増すと、いずれにせよ遅延が増えることになる。しかし,仮にラグがゼロであったとしても,スムージングが進むと,より小さなトレードをスキップすることになり,結果として,それぞれトレードの減少,利益の減少,ドローダウンの増加につながる......ということです。 絶望感... バランスカーブを見ながら、ハンドル(パラメータ)を回して、滑らかさを変更することができます。最適なものを見つけることで、ご指摘の2つの問題を解決できそうです。 TheXpert 2009.01.19 16:49 #17 Neutron >> :順次試してみるとか? 最初のバリアントを作り、それを分析する。 あれが好き、これが嫌い、だからこれとこれを取り除いて作り上げる、みたいな。 ただ、いろいろと混乱があるようで、原案は素晴らしいものだったんです。 Neutron 2009.01.19 17:40 #18 TheXpert писал(а)>> 順次試すべきでしょうか? 初期バージョンを作成し、それを分析する。 あれもこれも好き、これも嫌い、だからあれもこれも外して、ごちゃごちゃにする。 ただ、ここで混乱が見られるのは、原案が素晴らしかったからです。 ごちゃごちゃしない! 何もなければ、完璧なMAの基本的な条件を覚えておこう。 1.オリジナルVRへの近接性。この条件は、商X (図の緑線)と平滑化曲線 Y(青線)の距離の小ささに等しい。大きなサンプルでの平均では、これを満たす必要があると書ける。(X[i]-Y[i])^2-->最小値 2.MAの滑らかさ。この条件は、滑らかな曲線の隣り合うサンプル間の距離の小ささ:(Y[i]-Y[i-1])^2-->minに 等しい。 3.開いている方向(図の縦線の間)を考慮し、初期BPから切り出したピースで構成されるEquityカーブが大きくなるようにする。ポジション開度の符号はMAデリバティブの符号と等しくなります。我々の用語では、sign(Y[i]-Y[i-1])とする。 この場合、エクイティカーブは、閉じるべき位置の符号に従って突き合わされるコチエのピースで構成されることになる。このように実装することができます。コチラの第一差分系列(FDD)d[i]=X[i]-X[i-1] を構築してみよう。 とすると、エクイティカーブ()の速い成長は、そこから一次導関数を最大化する要件と等価である。dE[i]/dt=E[i]-E[i-1]= sign(Y[i]-Y[i-1])*(X[i]-X[i-1]) または小さいが許容できる、我々の場合は、ストレッチ{(Y[i]-Y[i-1])*(X[i]-X[i-1])}^2-->max ある式の最大化は反対の符号でその最小化に等しいことは明らかである。-{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min. それだけです。最小化のために必要な汎関数が得られる。 S=w1*(X-Y)^2+w2*(Y[i]-Y[i-1])^2-w3*{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min Y[i]( iは 現在の基準点)に対しての最小値を求める必要がある。 Our Masha! Registration for the MetaQuotes-Demo Integers 削除済み 2009.01.19 17:50 #19 素晴らしい!ある程度の期間、この解決策が見つかりました。次はどうする? TheXpert 2009.01.19 17:52 #20 Neutron >> : 散らからない! これ以上希望がないのであれば、完璧なMAの基本条件について記憶を呼び起こしましょう。 IMHOは、Yファンクションビューが欠けています。それとも、何か見落としがあったのでしょうか? mql4com>>: 素晴らしい、ある程度の期間、このような解決策を見つけることができました。じゃあ、何? 例えば?私たちは稼ぎます--収益性は対象機能に投資されます。 123456789...21 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
また、スムージングのレベルが高いと、収益性の向上という良い結果にはなりません。滑らかさを増すと、いずれにせよレイテンシーが増加することになる。しかし、仮に遅延がゼロであったとしても、滑らかさが増すと、小さな取引をスキップすることになり、取引量が減り、それぞれ利益が減り、その結果ドローダウンが増える......ということになるのです。
チャート上でも、理論上は取れるはずのかなり大きな取引の一部が取れず、利益が減っているのがよくわかる......。
また、スムージングのレベルが高いと、収益性の向上という良い結果にはなりません。滑らかさを増すと、いずれにせよレイテンシーが増加することになる。しかし,仮に遅延がゼロだと仮定しても,スムージングが進むと,より小さなトレードをスキップすることになり,その結果,トレードが減少し,それぞれ利益の減少,ドローダウンの増加につながる......ということになる。
最適なバリエーションに適応させる。
>> おっしゃるようなケースは、時間依存の指標ではすべて問題です。古典的な意味での時間をなくし、他の方法を使う。
私はとっくにこのようなTCはやめて他の方法を使っています・・・ただ、滑らかさを増すとどうなるかという意見として書き込みました ))))。
私はとっくにこのようなTCは諦めて他の方法を使っています・・・ただ、滑らかさを増すとどうなるかという意見として書き込みをしました )))))
手紙を書いてもいいですか?
さらに、このすべてに、遅延の増加によるエラー(損失)を追加する必要があり(利他的になる必要はありません)、利益の問題は空中でハングアップすることができます......))))
アイデアのオーサーシップについては議論してもいいと思う。おそらく、そのアイデアはMAと同じくらい古いものでしょう。:))
そして、一般的にこのテーマは私にとって興味深いものであり、私自身もそれに携わっています。当然ながら、すべてが絵のように美しいわけではありません。明らかに矢継ぎ早に足りない。
では、順番に。
私の考えでは、このようなシステムは、積極的なMMなしでは利益を得られないと思います。
さて、同志よ!- だから、正しい道を歩んでいるのです。
図は、ポジションの開閉方法を非常に模式的に示したものである。
議論の余地がある(2次導関数が0に等しい)ので、そちらからの反論が必要です。極限(一次導関数のゼロへの等化)については、議論の必要はなさそうです。
MAが引用に近いという要求と、同時に滑らかであるという要求は、相反するものではなく、互いに補完し合うものです(できない)。顕著な例として、通常の指数平均型EMAがあります。その再帰的な形式は、近接性と平滑性を同時に要求する汎関数の最小化から正確に得られる。
3.これは、メソッドの発展形と見ることができる。まず始めに、函数の形式に関する明白な要件について解答を得る必要がある。
Swetten さんが書き込みました>>1
失礼ですが、FZとは何でしょうか?
FZ - 位相差。DSPからの用語です。
TheXpert 2009年01月19日 14:45
対象機能は、アウトラインの参照に基づくものですか?
あまりにスムージングをしすぎると、良い結果が得られない。つまり、利益が増えてしまう。滑らかさを増すと、いずれにせよ遅延が増えることになる。しかし,仮にラグがゼロであったとしても,スムージングが進むと,より小さなトレードをスキップすることになり,結果として,それぞれトレードの減少,利益の減少,ドローダウンの増加につながる......ということです。
順次試してみるとか?
最初のバリアントを作り、それを分析する。
あれが好き、これが嫌い、だからこれとこれを取り除いて作り上げる、みたいな。
ただ、いろいろと混乱があるようで、原案は素晴らしいものだったんです。
順次試すべきでしょうか?
初期バージョンを作成し、それを分析する。
あれもこれも好き、これも嫌い、だからあれもこれも外して、ごちゃごちゃにする。
ただ、ここで混乱が見られるのは、原案が素晴らしかったからです。
ごちゃごちゃしない!
何もなければ、完璧なMAの基本的な条件を覚えておこう。
1.オリジナルVRへの近接性。この条件は、商X (図の緑線)と平滑化曲線 Y(青線)の距離の小ささに等しい。大きなサンプルでの平均では、これを満たす必要があると書ける。(X[i]-Y[i])^2-->最小値
2.MAの滑らかさ。この条件は、滑らかな曲線の隣り合うサンプル間の距離の小ささ:(Y[i]-Y[i-1])^2-->minに 等しい。
3.開いている方向(図の縦線の間)を考慮し、初期BPから切り出したピースで構成されるEquityカーブが大きくなるようにする。ポジション開度の符号はMAデリバティブの符号と等しくなります。我々の用語では、sign(Y[i]-Y[i-1])とする。 この場合、エクイティカーブは、閉じるべき位置の符号に従って突き合わされるコチエのピースで構成されることになる。このように実装することができます。コチラの第一差分系列(FDD)d[i]=X[i]-X[i-1] を構築してみよう。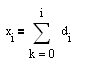 とすると、エクイティカーブ(
とすると、エクイティカーブ(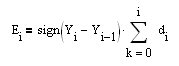 )の速い成長は、そこから一次導関数を最大化する要件と等価である。dE[i]/dt=E[i]-E[i-1]= sign(Y[i]-Y[i-1])*(X[i]-X[i-1]) または小さいが許容できる、我々の場合は、ストレッチ{(Y[i]-Y[i-1])*(X[i]-X[i-1])}^2-->max ある式の最大化は反対の符号でその最小化に等しいことは明らかである。-{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min.
)の速い成長は、そこから一次導関数を最大化する要件と等価である。dE[i]/dt=E[i]-E[i-1]= sign(Y[i]-Y[i-1])*(X[i]-X[i-1]) または小さいが許容できる、我々の場合は、ストレッチ{(Y[i]-Y[i-1])*(X[i]-X[i-1])}^2-->max ある式の最大化は反対の符号でその最小化に等しいことは明らかである。-{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min.
それだけです。最小化のために必要な汎関数が得られる。
S=w1*(X-Y)^2+w2*(Y[i]-Y[i-1])^2-w3*{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min
Y[i]( iは 現在の基準点)に対しての最小値を求める必要がある。
散らからない!
これ以上希望がないのであれば、完璧なMAの基本条件について記憶を呼び起こしましょう。
IMHOは、Yファンクションビューが欠けています。それとも、何か見落としがあったのでしょうか?
素晴らしい、ある程度の期間、このような解決策を見つけることができました。じゃあ、何?
例えば?私たちは稼ぎます--収益性は対象機能に投資されます。