微分積分、例 - ページ 6 12345678910111213...24 新しいコメント Aleksey Panfilov 2018.01.18 08:59 #51 レバレッジ72の4次多項式による平均化(4次EMA)、 3次放物線による異なるレバレッジへの外挿(3次多項式)。 a1_Buffer[i]=((open[i] - Znach) +5061600*a1_Buffer[i+1 ]-7489800 *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975; a5_Buffer[i+92]=a1_Buffer[i]; if(i<=1100) { for(z=92-1;z>=0;z--){ a5_Buffer[i+0+z]= 4*a5_Buffer[i+1+z] - 6*a5_Buffer[i+2+z] + 4*a5_Buffer[i+3+z] - 1*a5_Buffer[i+4+z]; }} a2_Buffer[i+20]=a5_Buffer[i+20]; a3_Buffer[i+38]=a5_Buffer[i+38]; a4_Buffer[i+56]=a5_Buffer[i+56]; a6_Buffer[i+74]=a5_Buffer[i+74]; 第1図はプロット図、第2図では再描画しない 線はすべて最後の値まで描画される。地下のインジケータは、設定されたラインのオフセットのみが異なる。 ファイル: 2018_01_18_EMA_Polynom_s4_s3_p72_6v.1p.mq4 17 kb 2018_01_18_EMA_Polynom_s4_s3_p72_9v.21.mq4 17 kb Aleksey Panfilov 2018.01.18 09:06 #52 レバレッジ72の4次多項式による平均化(4次EMA)、4次多項式を用いた異なるレバレッジへの外挿。 a1_Buffer[i]=((open[i] - Znach) +5061600*a1_Buffer[i+1 ]-7489800 *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975; a5_Buffer[i+92]=a1_Buffer[i]; if(i<=1100) { for(z=92-1;z>=0;z--){ a5_Buffer[i+0+z]= 5*a5_Buffer[i+1+z] - 10*a5_Buffer[i+2+z] + 10*a5_Buffer[i+3+z] - 5*a5_Buffer[i+4+z] + 1*a5_Buffer[i+5+z]; }} a2_Buffer[i+20]=a5_Buffer[i+20]; a3_Buffer[i+38]=a5_Buffer[i+38]; a4_Buffer[i+56]=a5_Buffer[i+56]; a6_Buffer[i+74]=a5_Buffer[i+74]; 第1図はプロット図、第2図では再描画しない 線はすべて最後の値まで描画される。地下のインジケータは、設定されたラインのオフセットのみが異なる。 ファイル: 2018_01_18_EMA_Polynom_s4_s4_p72_2v.1t.mq4 17 kb 2018_01_18_EMA_Polynom_s4_s4_p72_8v.2w.mq4 17 kb Nikolai Semko 2018.01.18 15:56 #53 アレクセイ、無料でアドバイスとヒントをあげられるよ。左にずれるというのは、なんというか......。- という、ありがたくない仕事です。あなたのスレを見ている人たちから罵声を浴びるだけでしょう。ちなみに、自分のスレッドで一人で自慢しているのも、その理由の一つです。 しかし、1つの変曲点を持つ周期線を左に半波ずらすには(というより、局所的な最小値と最大値の間に1つの変曲点しかない場合)、実際にずらすことなく、その関数の微分を使うことができるのです。たしかに、実際にシフトしているわけではなく、本質的には関数の導関数は、接線の角度である。buf[i]-buf[i+1] と単純に計算される。ここでは、例えば、正弦波の1次微分と2次微分を示します。関数自体の変曲点が、その導関数の局所的な最大値、最小値になる。 Aleksey Panfilov 2018.01.18 18:31 #54 ニコライ・セムコアレクセイ、無料でアドバイスとヒントをあげるよ。先ほどから言っているように、左にシフトをかけるというのは、なんというか......。- という、ありがたくない仕事です。あなたのスレを見ている人たちから罵声を浴びるだけでしょう。ちなみに、自分のスレッドで一人で自慢しているのも、その理由の一つです。 しかし、1つの変曲点を持つ周期線を左に半波ずらすには(というより、局所的な最小値と最大値の間に1つの変曲点しかない場合)、実際にずらすことなく、その関数の微分を使うことができるのです。たしかに、実際にシフトしているわけではなく、本質的にはそうなのですが。関数の導関数は、接線の角度である。buf[i]-buf[i+1] と単純に計算される。ここでは、例えば、正弦波の1次微分と2次微分を示します。関数自体の変曲点が、その導関数の局所的な最大値、最小値となる。もちろん、微分するごとにサイングラフは1/4周期分、左にずれていきます。だから、比較するときには、人為的なラインシフトを排除した。このことは、ここ数回の記事の2番目の数字で わかると思います。細いグレーの線以外は、最後のバーに描かれ、再描画されない。また、グラフが左にシフトしているのは、外挿によるものです。 そして、これらのラインは実際にまだ区別することができ、私たちの場合は、プロトタイプに あった最初と2番目の違いを取り除くことができます。:)))左へのシフトは、工事用ラインを含むすべてのラインを全体像に結びつけ、全体のスキームを見るために使用しました。 Nikolai Semko 2018.01.18 19:00 #55 アレクセイ・パンフィロフもちろん、微分するたびにサイングラフは1/4周期分、左にずれていきます。だから、比較するときは、人為的なラインずれを排除したんです。このことは、ここ数回の記事の2番目の数字で わかると思います。細いグレーの線以外は、最後のバーに描かれ、再描画されません。また、グラフが左にシフトしているのは、外挿によるものです。左へのシフトは、工事線を含むすべての線を全体像につなげ、大枠を示すために使用しました。上のグラフは左にずれてテールが描き直されるため、無視することができる。そして下の方はラグがあり平凡な印象です。この騒ぎは何なんだ? Aleksey Panfilov 2018.01.18 19:06 #56 ニコライ・セムコ 上のチャートは左にずれており、テールがオーバードローになっているので無視できます。そして下の方はラグがあり平凡な印象です。では、この騒動に何の意味があるのでしょうか?))))進めながら」見ます。今のところ、すべて順調です。)) Nikolai Semko 2018.01.18 22:58 #57 ニコライ・セムコアレクセイ、無料でアドバイスとヒントをあげるよ。私はすでに、左にシフトすることは、なんというか、控えめな表現なのだと言っているのですが.- という、ありがたくない仕事です。あなたのスレを見ている人たちから罵声を浴びるだけでしょう。ちなみに、自分のスレッドで一人で自慢しているのも、その理由の一つです。 しかし、1つの変曲点を持つ周期線を左に半波ずらすには(というより、局所的な最小値と最大値の間に1つの変曲点しかない場合)、実際にずらすことなく、その関数の微分を使うことができるのです。たしかに、実際にシフトしているわけではなく、本質的にはそうなのですが。関数の導関数は、接線の角度である。buf[i]-buf[i+1] と単純に計算される。ここでは、例えば、正弦波の1次微分と2次微分を示します。関数自体の変曲点が、その導関数の局所的な最大値、最小値となる。ここでは、このアプローチの可能な実装の一つを紹介します。再描画やシフトはしない。 これはあなたの線の2次微分です。 ファイル: Banzai.mq4 5 kb Banzai.mq5 6 kb Nikolai Semko 2018.01.18 23:36 #58 時には非常に相関性が高く、ラグがない場合もある Maxim Kuznetsov 2018.01.19 01:09 #59 ニコライ・セムコアレクセイ、無料でアドバイスとヒントをあげられるよ。先ほどから言っているように、左にシフトをかけるというのは、なんと いうか......。- という、ありがたくない仕事 です。あなたのスレを見ている人たちから罵声を浴びるだけでしょう。ちなみに、自分のスレッドで一人で自慢しているのも、その理由の一つです。 しかし、1つの変曲点を持つ周期線を左に半波ずらすには(というより、局所的な最小値と最大値の間に1つの変曲点しかない場合)、実際にずらすことなく、その関数の微分を使うことができるのです。たしかに、実際にシフトしているわけではなく、本質的にはそうなのですが。関数の導関数は、接線の角度である。buf[i]-buf[i+1] と単純に計算される。ここでは、例えば、正弦波の1次微分と2次微分を示します。関数自体の変曲点が、その導関数の局所的な最大値、最小値となる。今日は機嫌がいいんだ。Alg. on "shift left" (なんというネーミングでしょう :).1.高速と低速の2つのSMAを取る。2.半周期左にずらす(各自)。3.ということに驚いています。3.0の波形が渦を巻いている。3.1. 極限直前で速い方が遅い方を上にずらす(もっと早い場合もある)。3.2. "ペア "クロスオーバー(極値の前で上向き、後で下向き)4.バーをリアルタイムに戻すが、(n2とは異なり)同じ量だけシフトさせる。一方は0で終わり、もう一方は右に強く出ていく 5.さて、過去の極限と前回のクロスオーバーを見たところで、すでにクロスしているところを見ます。それをもとに、明らかな誤検出を排除して、かなり良いエントリーができるようになりました。 Nikolai Semko 2018.01.19 02:19 #60 マキシム・クズネツォフ今日は機嫌がいいAlg. on "shift left" (なんというネーミングでしょう :)1. 古典に従って、速いものと遅いものの2つのSMAを取る。2.半周期左にずらす(各自)。3.ということに驚いています。3.0の波形が渦を巻いている。3.1. 極限直前で速い方が遅い方を上にずらす(もっと早い場合もある)。3.2. "ペア "クロスオーバー(極値の前で上向き、後で下向き)4.バーをリアルタイムに戻すが、(n2とは異なり)同じ量だけシフトさせる。一方は0で終わり、もう一方は右に強く出ていく 5.さて、過去の極限と前回のクロスオーバーを見たところで、すでにクロスしているところを見ます。それをもとに、明らかな誤検出を排除し、かなり良いエントリーをすることができます。もしかしたら、何かあるのかもしれない。しかし、それは左遷のアルゴリズムではなく、右遷のアルゴリズムである。 12345678910111213...24 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
レバレッジ72の4次多項式による平均化(4次EMA)、 3次放物線による異なるレバレッジへの外挿(3次多項式)。
第1図はプロット図、第2図では再描画しない 線はすべて最後の値まで描画される。
地下のインジケータは、設定されたラインのオフセットのみが異なる。
レバレッジ72の4次多項式による平均化(4次EMA)、4次多項式を用いた異なるレバレッジへの外挿。
第1図はプロット図、第2図では再描画しない 線はすべて最後の値まで描画される。
地下のインジケータは、設定されたラインのオフセットのみが異なる。
アレクセイ、無料でアドバイスとヒントをあげられるよ。
左にずれるというのは、なんというか......。- という、ありがたくない仕事です。あなたのスレを見ている人たちから罵声を浴びるだけでしょう。ちなみに、自分のスレッドで一人で自慢しているのも、その理由の一つです。
しかし、1つの変曲点を持つ周期線を左に半波ずらすには(というより、局所的な最小値と最大値の間に1つの変曲点しかない場合)、実際にずらすことなく、その関数の微分を使うことができるのです。たしかに、実際にシフトしているわけではなく、本質的には関数の導関数は、接線の角度である。buf[i]-buf[i+1] と単純に計算される。
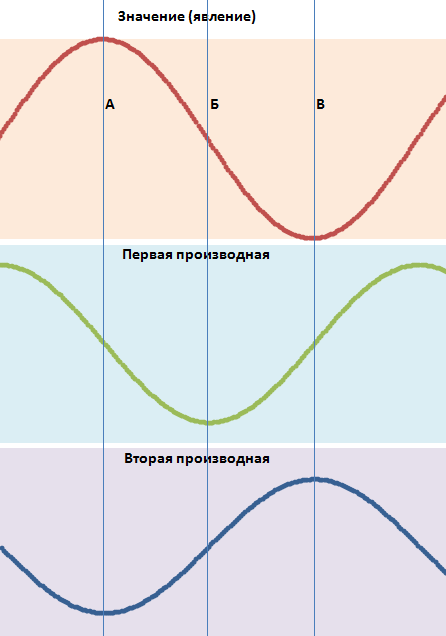
ここでは、例えば、正弦波の1次微分と2次微分を示します。関数自体の変曲点が、その導関数の局所的な最大値、最小値になる。
アレクセイ、無料でアドバイスとヒントをあげるよ。
先ほどから言っているように、左にシフトをかけるというのは、なんというか......。- という、ありがたくない仕事です。あなたのスレを見ている人たちから罵声を浴びるだけでしょう。ちなみに、自分のスレッドで一人で自慢しているのも、その理由の一つです。
しかし、1つの変曲点を持つ周期線を左に半波ずらすには(というより、局所的な最小値と最大値の間に1つの変曲点しかない場合)、実際にずらすことなく、その関数の微分を使うことができるのです。たしかに、実際にシフトしているわけではなく、本質的にはそうなのですが。関数の導関数は、接線の角度である。buf[i]-buf[i+1] と単純に計算される。
ここでは、例えば、正弦波の1次微分と2次微分を示します。関数自体の変曲点が、その導関数の局所的な最大値、最小値となる。
もちろん、微分するごとにサイングラフは1/4周期分、左にずれていきます。
だから、比較するときには、人為的なラインシフトを排除した。このことは、ここ数回の記事の2番目の数字で わかると思います。細いグレーの線以外は、最後のバーに描かれ、再描画されない。また、グラフが左にシフトしているのは、外挿によるものです。
そして、これらのラインは実際にまだ区別することができ、私たちの場合は、プロトタイプに あった最初と2番目の違いを取り除くことができます。:)))
左へのシフトは、工事用ラインを含むすべてのラインを全体像に結びつけ、全体のスキームを見るために使用しました。
もちろん、微分するたびにサイングラフは1/4周期分、左にずれていきます。
だから、比較するときは、人為的なラインずれを排除したんです。このことは、ここ数回の記事の2番目の数字で わかると思います。細いグレーの線以外は、最後のバーに描かれ、再描画されません。また、グラフが左にシフトしているのは、外挿によるものです。
左へのシフトは、工事線を含むすべての線を全体像につなげ、大枠を示すために使用しました。
上のグラフは左にずれてテールが描き直されるため、無視することができる。そして下の方はラグがあり平凡な印象です。この騒ぎは何なんだ?
上のチャートは左にずれており、テールがオーバードローになっているので無視できます。そして下の方はラグがあり平凡な印象です。では、この騒動に何の意味があるのでしょうか?
))))
進めながら」見ます。
今のところ、すべて順調です。))
アレクセイ、無料でアドバイスとヒントをあげるよ。
私はすでに、左にシフトすることは、なんというか、控えめな表現なのだと言っているのですが.- という、ありがたくない仕事です。あなたのスレを見ている人たちから罵声を浴びるだけでしょう。ちなみに、自分のスレッドで一人で自慢しているのも、その理由の一つです。
しかし、1つの変曲点を持つ周期線を左に半波ずらすには(というより、局所的な最小値と最大値の間に1つの変曲点しかない場合)、実際にずらすことなく、その関数の微分を使うことができるのです。たしかに、実際にシフトしているわけではなく、本質的にはそうなのですが。関数の導関数は、接線の角度である。buf[i]-buf[i+1] と単純に計算される。
ここでは、例えば、正弦波の1次微分と2次微分を示します。関数自体の変曲点が、その導関数の局所的な最大値、最小値となる。
ここでは、このアプローチの可能な実装の一つを紹介します。再描画やシフトはしない。 これはあなたの線の2次微分です。
時には非常に相関性が高く、ラグがない場合もある
アレクセイ、無料でアドバイスとヒントをあげられるよ。
先ほどから言っているように、左にシフトをかけるというのは、なんと いうか......。- という、ありがたくない仕事 です。あなたのスレを見ている人たちから罵声を浴びるだけでしょう。ちなみに、自分のスレッドで一人で自慢しているのも、その理由の一つです。
しかし、1つの変曲点を持つ周期線を左に半波ずらすには(というより、局所的な最小値と最大値の間に1つの変曲点しかない場合)、実際にずらすことなく、その関数の微分を使うことができるのです。たしかに、実際にシフトしているわけではなく、本質的にはそうなのですが。関数の導関数は、接線の角度である。buf[i]-buf[i+1] と単純に計算される。
ここでは、例えば、正弦波の1次微分と2次微分を示します。関数自体の変曲点が、その導関数の局所的な最大値、最小値となる。
今日は機嫌がいいんだ。
Alg. on "shift left" (なんというネーミングでしょう :).
1.高速と低速の2つのSMAを取る。
2.半周期左にずらす(各自)。
3.ということに驚いています。
3.0の波形が渦を巻いている。
3.1. 極限直前で速い方が遅い方を上にずらす(もっと早い場合もある)。
3.2. "ペア "クロスオーバー(極値の前で上向き、後で下向き)
4.バーをリアルタイムに戻すが、(n2とは異なり)同じ量だけシフトさせる。一方は0で終わり、もう一方は右に強く出ていく
5.さて、過去の極限と前回のクロスオーバーを見たところで、すでにクロスしているところを見ます。それをもとに、明らかな誤検出を排除して、かなり良いエントリーができるようになりました。
今日は機嫌がいい
Alg. on "shift left" (なんというネーミングでしょう :)
1. 古典に従って、速いものと遅いものの2つのSMAを取る。
2.半周期左にずらす(各自)。
3.ということに驚いています。
3.0の波形が渦を巻いている。
3.1. 極限直前で速い方が遅い方を上にずらす(もっと早い場合もある)。
3.2. "ペア "クロスオーバー(極値の前で上向き、後で下向き)
4.バーをリアルタイムに戻すが、(n2とは異なり)同じ量だけシフトさせる。一方は0で終わり、もう一方は右に強く出ていく
5.さて、過去の極限と前回のクロスオーバーを見たところで、すでにクロスしているところを見ます。それをもとに、明らかな誤検出を排除し、かなり良いエントリーをすることができます。
もしかしたら、何かあるのかもしれない。しかし、それは左遷のアルゴリズムではなく、右遷のアルゴリズムである。