Il fenomeno di San Pietroburgo. I paradossi della teoria della probabilità. - pagina 5
Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
Ecco, ho fatto i conti.
per 100.000 giochi è un numero di 8,32 rubli.
per un milione di giochi questo numero è di 25,76 rubli.
Più giochi, più alto è il numero.
È come la martingala: più giochi, più alta è la probabilità di perdere.
Aiutatemi con il file di questo post, non riesco a capirlo, la colonna D ha la formula =A(A1)
Puzzle matematici e divertimento
Questo libro del famoso divulgatore scientifico americano M. Gardner ha un sacco di problemi molto divertenti e puzzle da diversi rami della matematica. Una selezione di successo del materiale, una forma completamente insolita di presentazione e l'umorismo sottile dell'autore porterà grande piacere a una vasta gamma di lettori - gli amanti della matematica che vogliono spendere utilmente il loro tempo libero
Grazie, Oleg, impressionante))
per ottenere un numero casuale tra 0 e 6 (uno su 7):
- considera limite=RAND_MAX - (RAND_MAX%7) ; il massimo multiplo di 7 nell'intervallo 0...RAND_MAX
- usare RDS fino ad ottenere r<limite; cioè se il "numero casuale" è superiore al limite, non possiamo farci niente - prendiamo
- risultato = r % 7 o (nel bene e nel male) r * 7 / limite
qualcosa come questo :-) potrebbe essere sbagliato +-1,
Nel nostro caso RAND_MAX = 32767 è diviso per 7 senza resto, quindi il tuo esempio non è molto buono. Se consideriamo un caso generale, otterremo uno skew di probabilità a favore di numeri più grandi del resto.
Cioè, se diciamo RAND_MAX%7 = 4, otterremo più spesso 5 e 6. Ecco perché non bisogna scartare nulla. Tutto deve essere preso in considerazione.
Ecco, ho fatto i conti.
per 100.000 giochi, il numero è di 8,32 rubli.
per un milione di giochi, il numero è di 25,76 rubli.
Più giochi, più alto è il numero.
È come la martingala: più si gioca, più alta è la possibilità di perdere.
Il punto del gioco: per entrare nel gioco è necessario un deposito e il gioco della moneta dura fino a quando appare la prima aquila (un gioco una tantum), 1-gatto vince quando un'aquila appare nel primo rullo, se c'era croce e un'aquila appare nel secondo rullo, l'importo vincente è raddoppiato, e così via all'infinito, fino a quando appare un'aquila. Probabilità di vincere 1 ducato 0,5, 2-0,25, 4-0,125, ecc. Quindi, è possibile vincere all'infinito, e giocare all'infinito, se la somma del banco è infinita.
Forum sul trading, sistemi di trading automatico e test di strategie di trading
Il fenomeno di San Pietroburgo. I paradossi della teoria della probabilità.
Novaja, 2018.10.24 10:02
Il significato del gioco: per entrare nel gioco è necessario un deposito e il gioco della moneta dura fino a quando appare la prima aquila (un gioco una tantum), 1-doppia vincita quando l'aquila appare nel primo rullo, se c'era croce e l'aquila è apparsa nel secondo rullo, l'importo della vincita è raddoppiato, e così all'infinito, fino a quando l'aquila appare. Probabilità di vincere 1 ducato-0,5, 2-0,25, 4-0,125 etc., quindi si può vincere all'infinito, e giocare all'infinito, se il piatto è infinito.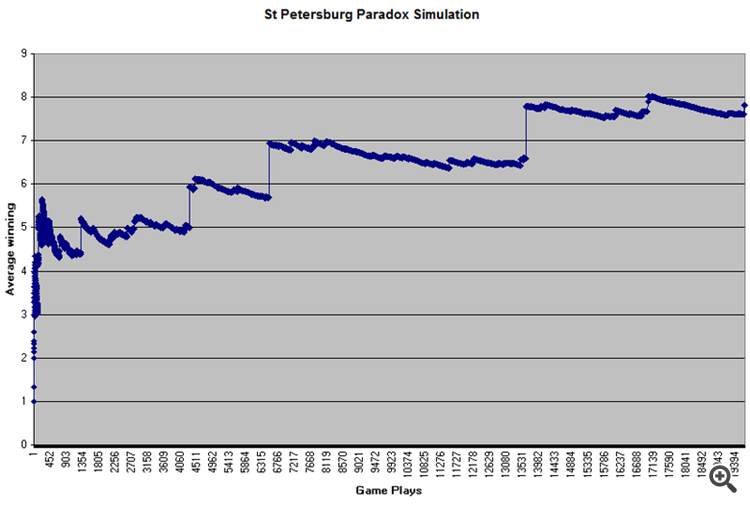
Aiutatemi con il file di questo post, non capisco la colonna D, ha la formula =A(A1)
In breve, conta su quale goccia è caduta un'aquila.
Cosa succede se ci pensi?
Che ne dici di non scrivere post senza senso?