Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
Oh, mio Dio! Non pensavo che sarebbe successo così)).
Oh, mio Dio! Non pensavo che sarebbe successo così)))
No, non credo a questi indicatori.
Mentono.
Non credere agli indicatori. Fidati di me.
No, non mi fido di questi indicatori.
Mentono.
Non credere agli indicatori. Fidati di me.
Non è quello che ha detto Müller: non ci si può fidare di nessuno... Io posso.)
Müller non la mette così: non ci si può fidare di nessuno... Io posso.)
Sei riuscito a farmi ridere per l'undicesima volta oggi)). Dieci volte quando si legge il prossimo thread.
Ma ci si può certamente fidare di me. Non sono Mueller))
Questo è il risultato della determinazione della differenza tra gli estremi in funzione del cambiamento del valore di soglia della ZZ di Kagi. Figura b) - curva cumulativa.
Lo stesso per la ZZ di Renko.
Ho notato una caratteristica interessante: la distribuzione Chi-quadro:
Vedi, a k=1, c'è una somiglianza con la ZZ di Kagi, a k=2, un esponente, esattamente come nel grafico ZZ di Renko.
La distribuzione Chi-quadro tende alla normalità all'aumentare di k.
Beh, non so...
La funzione è interessante, ma come approfittarne? È difficile suggerire qualcosa, dato che non sono bravo in Kagi o Renko dalla parola "per niente".
Ma ci proverò.
1. Bisogna rinunciare al desiderio di ottenere una distribuzione normale e cercare per secoli di trovarla. Lavorare con i modelli già trovati è già un affare molto, molto grande.
2.https://en.wikipedia.org/wiki/Generalized_normal_distribution
3. In parole povere, xy-squared con k=1 è la somma dei quadrati dei NA distribuiti normalmente, xy-squared con k=2 è la somma dei NA con una distribuzione Laplace
4. Ero interessato al caso con k=2, perché gli studi mostrano che il mercato è dominato dalla distribuzione di Laplace (doppia geometrica per essere precisi)
5. Non è chiaro qui - in questi Renko cosa conta? La somma delle differenze (Alto-Basso)?
6. Se è così - allora la differenza (High-Low) in Renko è SV appartenente alla distribuzione di Laplace - dovrebbe essere confermato sperimentalmente.
7. Poi la somma delle differenze (Alto-Basso) nella finestra scorrevole (per un certo volume di campione) forma xy-quadrato con k=2 con funzione quantile nota
https://keisan.casio.com/exec/system/1180573197
8. Aspettiamo l'uscita (High-Low) nella finestra scorrevole oltre i limiti di un intervallo di confidenza per un certo quantile ed entriamo nel commercio.
Beh, questo è solo un abbozzo di algoritmo, solo per sviluppare il soggetto e niente di più :)))
5. Non è chiaro qui - in questi Renko, cosa conta? La somma delle differenze (High-Low)?
7. Quindi la somma delle differenze (Alto-Basso) in una finestra scorrevole (per una certa dimensione del campione) forma un quadrato xy con k=2 con una funzione quantile nota
https://keisan.casio.com/exec/system/1180573197
8. Attendere l'uscita (High-Low) nella finestra scorrevole oltre i confini dell'intervallo di confidenza per un certo quantile ed entrare nel commercio.
5. Renko considera lo sfondamento dell'intervallo impostato dal "mattone Renko" sul valore di 1 "mattone", inoltre lo sfondamento dovrebbe essere sul valore del "mattone", cioè "mattone" 10 punti, per disegnare un nuovo mattone Renko, il prezzo dovrebbe passare sopra la barra Renko già formata 10п+1п (o sotto su 10п+1п) e poi un nuovo "mattone" sarà disegnato. Cioè, in sostanza, il prezzo è discretizzato senza tempo dal valore del "mattone Renko". Renko rimuove le componenti di rumore del prezzo ma come ogni filtro c'è un ritardo, per disegnare una nuova barra Renko il prezzo deve passare attraverso 2 intervalli = 2 altezze di mattoni Renko
7,8 è un indicatore ATR, quello che scrivi è di solito chiamato un breakdown di volatilità, ma c'è un eterno problema - il periodo dell'ATR, se il periodo è piccolo, ci sarà rumore, se il periodo è lungo, ci sarà ritardo
Qui
Forum sul trading, sistemi di trading automatico e strategie di trading di prova
Pastori ZigZags
Novaja, 2018.08.26 23:22
Questo è il risultato della determinazione della differenza tra gli estremi in funzione del cambiamento della soglia per ZZ Kagi. Figura b) - curva cumulativa.
Lo stesso per Renko ZZ.
Ho notato una caratteristica interessante: la distribuzione Chi-quadro:
Vedi, a k=1, c'è una somiglianza con la ZZ di Kagi, a k=2, esponente, esattamente lo stesso del grafico ZZ di Renko.
La distribuzione Chi-quadro tende alla normalità con l'aumento di k.
Novaja parla di qualche differenza tra gli estremi... Riguardo allo spread (High-Low) o qualcosa del genere? Non riesco a capire... È troppo asciutto e scritto in modo conciso...
Ma, sembra un quadrato xy - è per questo che sono interessato. Trovare schemi chiari è molto raro.
Non so...
La funzione è interessante, ma come si fa ad approfittarne? È difficile suggerire qualcosa, considerando che non sono bravo né in Kagi né in Renko dalla parola "affatto".
Ma ci proverò.
1. Bisogna rinunciare al desiderio di ottenere una distribuzione normale e cercare per secoli di trovarla. Lavorare con i modelli già trovati è già un affare molto, molto grande.
2.https://en.wikipedia.org/wiki/Generalized_normal_distribution
3. In parole povere, xy-squared con k=1 è la somma dei quadrati dei NA distribuiti normalmente, xy-squared con k=2 è la somma dei NA con una distribuzione Laplace
4. Ero interessato al caso con k=2, perché gli studi mostrano che il mercato è dominato dalla distribuzione di Laplace (doppia geometrica per essere precisi)
5. Non è chiaro qui - in questi Renko cosa conta? La somma delle differenze (Alto-Basso)?
6. Se è così - allora la differenza (High-Low) in Renko è SV appartenente alla distribuzione di Laplace - dovrebbe essere confermato sperimentalmente.
7. Poi la somma delle differenze (Alto-Basso) nella finestra scorrevole (per un certo volume di campione) forma xy-quadrato con k=2 con funzione quantile nota
https://keisan.casio.com/exec/system/1180573197
8. Aspettiamo l'uscita (High-Low) nella finestra mobile oltre i limiti di un intervallo di confidenza per un certo quantile ed entriamo nel commercio.
Beh, questo è solo un algoritmo approssimativo, solo per sviluppare il soggetto e niente di più :)Cgfcb,j
Grazie mille, ottimo commento.
Qualche parola sulla costruzione della zz. La variante di Kagi.
Il blu mostra il grafico a tick, la soglia è 3p. Se l'opposto è maggiore di 3 pip si traccia un estremo, altrimenti si va oltre. Cioè le oscillazioni possono contenere 2,66; 3,66; n numero di tali soglie (segmenti) con valori frazionari. Questo valore frazionario viene scartato nella costruzione di tipo Renko, ma il principio è lo stesso. Cioè valori interi 2,3, ecc. Così vediamo come i vertici frazionari non sono presi in considerazione nella costruzione. Nell'immagine qui sotto è una variante di Renko.
Ora penso che la differenza sia chiara. Quindi, la frequenza di apparizione del rapporto tra la lunghezza dell'oscillazione e il valore di soglia (segmento di 3p) per Kagi: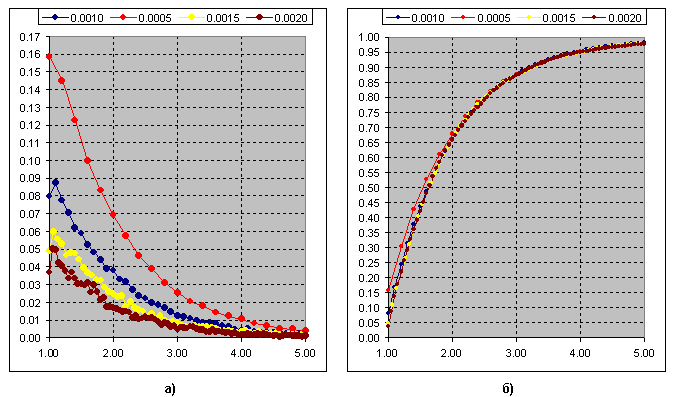
Fig.b) Somma cumulativa delle curve. La distribuzione Chi-quadrato a k=1 si adatta a questa curva.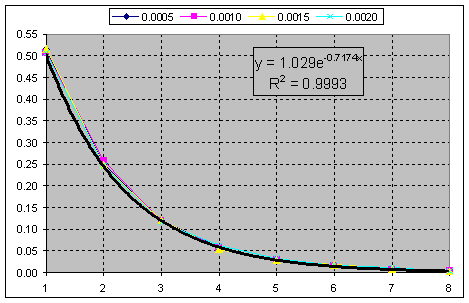
E questa è la somma cumulativa della frequenza di occorrenza del rapporto di oscillazione alla soglia (segmento) per la costruzione Renko. Chi-quadrato a k=2.
Cioè dobbiamo solo scartare le parti frazionarie e ottenere un esponente puro.
Grazie mille, ottimo commento.
Qualche parola sulla costruzione della zz. La variante di Kagi.
Il blu mostra il grafico a tick, soglia - 3p. Se l'opposto è maggiore di 3 pip si traccia un estremo, altrimenti si va oltre. Cioè le oscillazioni possono contenere 2,66; 3,66; n numero di tali soglie (segmenti) con valori frazionari. Questo valore frazionario viene scartato nella costruzione di tipo Renko, ma il principio è lo stesso. Cioè valori interi 2,3, ecc. Così vediamo come i vertici frazionari non sono presi in considerazione nella costruzione. Nell'immagine qui sotto è una variante di Renko.
Ora penso che la differenza sia chiara. Quindi, la frequenza di apparizione del rapporto tra la lunghezza dell'oscillazione e il valore di soglia (segmento di 3p) per Kagi:
Fig.b) Somma cumulativa delle curve. La distribuzione Chi-quadrato a k=1 si adatta a questa curva.
E questa è la somma cumulativa della frequenza di occorrenza del rapporto di oscillazione alla soglia (segmento) per la costruzione Renko. Chi-quadrato a k=2.
Cioè dovete solo scartare le parti frazionarie perché ottenete un esponente puro.
Altalene... Eh-mah... :)))
OK. Non mi addentrerò nella terminologia. Non c'è tempo.
Abbiamo l'esponente più puro su qualsiasi cosa.
La somma di queste componenti sarà una distribuzione binomiale negativa (la distribuzione Erlang per NE continua) di nuovo, sottolineo, con del famoso dispersione. Il limite è la distribuzione normale che state cercando.