Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Bonjour Mladen
quand vous aurez la moitié d'une chance
s'il vous plaît, pouvez-vous faire votre HMA original coloré nrp en MTF et peut-il avoir interpolate
à moins que ce soit déjà disponible et que je l'ai manqué
Merci beaucoup.
J'apprécie beaucoupWR1
Une version de la moyenne mobile Hull multi time frame non repeinte est postée sur ce post : https://www.mql5.com/en/forum/174961/page3 (avec les paramètres par défaut (HMASpeed==2) c'est la même chose que la HMA nrp "normale").
Bonjour MLaden,
Je crois que je vous comprends et suis d'accord avec vous pour le calcul des valeurs historiques d'une échelle de temps supérieure. Nous n'avons qu'un nombre limité de barres correspondant à des points de données supplémentaires (barres sur l'échelle de temps inférieure) donc nous avons besoin d'interpolation, linéaire quadratique etc. pour remplir les barres manquantes ou utiliser une fonction d'étape pour couvrir les deux valeurs de l'échelle de temps supérieure sur l'échelle de temps inférieure. Cependant, une fois que l'indicateur a démarré, nous obtenons des points de données tick par tick qui s'appliquent également aux cadres temporels inférieurs et supérieurs. Je me demandais s'il existait un indicateur qui calculait et stockait les valeurs supérieures pour les barres inférieures intermédiaires. Par exemple, en utilisant un cadre temporel H1 et H4. Nous pouvons calculer la barre H4 et ensuite interpoler linéairement les trois valeurs manquantes des barres inférieures en utilisant la différence proportionnelle entre la barre N et la barre N+1 pour les barres qui ont eu lieu avant le moment où l'indicateur a commencé. Ce que je me demande, c'est si au lieu d'interpoler les barres manquantes après le démarrage de l'indicateur, nous sauvegardons et stockons les valeurs intermédiaires des barres horaires de l'image supérieure. Avec cette approche, nous aurions les valeurs exactes pour les trois barres d'intervalle. Je reconnais qu'il y aura une discontinuité entre les valeurs intermédiaires historiques pour le cadre temporel supérieur avant le démarrage de l'indicateur. Ainsi, si un indicateur H4 passe de 1,0 à la barre N+1 à 1,4 à la barre N, les valeurs intermédiaires interpolées seraient 1,1, 1,2, 1,3. Cependant, en réalité, les valeurs pourraient être 1.0 1.3, 1.5, 1.4 en fonction des valeurs aux temps N, N+1, N+2, N+3.
Je suppose que ce que je veux dire en fait, c'est pourquoi utiliser l'intervalle de temps supérieur pour un indicateur MTF et utiliser plutôt les points de données de l'intervalle de temps inférieur, mais avancer l'indicateur supérieur toutes les Nième barres au lieu de toutes les barres et utiliser les valeurs réelles pour chacun des intervalles.
Si vous avez un indicateur MTF simple utilisant une EMA, pouvez-vous le poster et je l'utiliserai pour tester ma théorie et le posterai en retour.
Tzuman
Salut Mladen,
Eh bien, j'ai testé et je suis d'accord avec vous, ce n'est pas vraiment bon par rapport aux autres MA de Hull.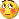
Comme je l'ai dit, pour moi la meilleure moyenne mobile doit être rapide ET régulière.
Je teste donc différentes MA (sur mon graphique) qui me semblent intéressantes
Adaptive T3 (bleu/orange)
NonlagMA (vert/rouge)
JJMA (seulement vert, je n'ai pas de JJMA bicolore)
Et une coque
(Désolé, difficile d'être clair car je ne peux pas déplacer les lignes)
Le but du jeu était d'essayer de comparer les MA (avec des périodes différentes bien sûr).
Pour moi
Adaptive T3 Lisse 4/5 Rapide 4/5
Nonlag MA Lisse 3/5 Rapide 5/5
Hull Smooth 3/5 Fast 3/5
JJMA Lisse 4/5 Rapide 4/5
Donc, juste une idée, je pense que ça pourrait être intéressant de faire une coque adaptée par T3 adaptatif (gloups...), et une coque adaptée par JJMA. Pouvez-vous les faire s'il vous plaît ?
Je compare aussi 3 JMA (Spiggy, Starlight et Kositsin). Comme vous le voyez sur le graphique, le meilleur est clairement le Kositsin en vert (JJMA), et le pire le Starlight (et repaint)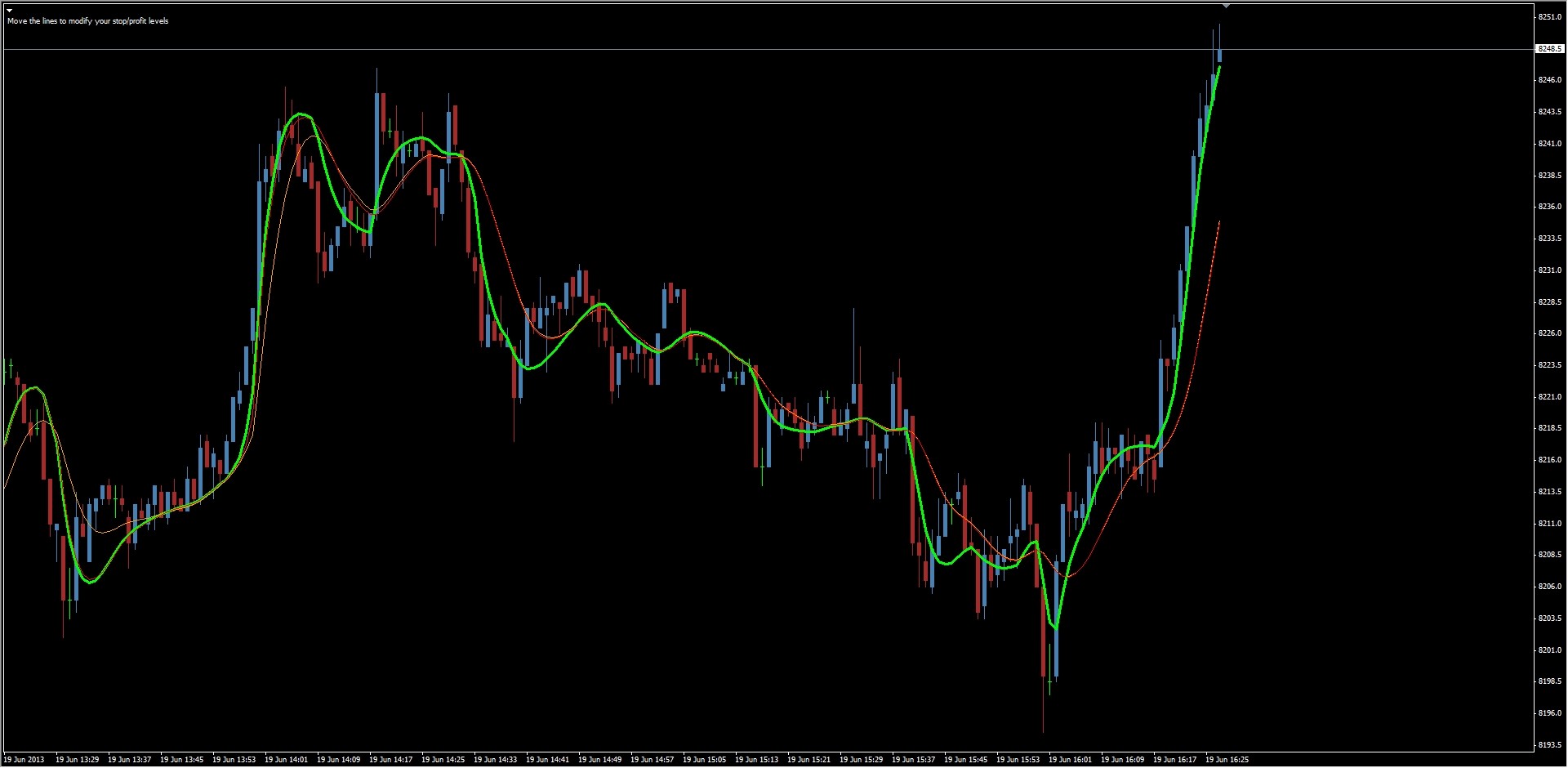 Le T3 adaptatif et le JJMA que j'utilise pour le graphique et pour créer ces Coques adaptatives
Le T3 adaptatif et le JJMA que j'utilise pour le graphique et pour créer ces Coques adaptatives
jjma.mq4
Adaptive_t3_mladen.mq4
Mille fois merci pour la communauté Mladen
Bon week-end
Zilliq
Merci beaucoup Mladen, j'essaierai quand je serai de retour à la maison.
Je vais comparer avec une MA de Hull et votre NonlagMA.
Tout à fait d'accord avec vous : Je préfère quand il y a une certaine douceur. Rapidité et douceur, c'est si beau...
Savez-vous s'il existe une variation de la coque T3 ?
Et peut-être que c'est stupide, mais vous créez une moyenne mobile de Hull adaptée avec une Ma nonlag, et vous n'en êtes pas satisfait. Pensez-vous que le résultat (plus lisse) sera meilleur avec une NonlagMa adaptée avec une Hull MA ?
Au revoir et bon week-end
Zilliq
WR1 Une version de la moyenne mobile Hull non repeinte est postée à cet endroit : https://www.mql5.com/en/forum/174961/page3 (avec les paramètres par défaut (HMASpeed==2) c'est la même que la HMA nrp "normale").
Merci beaucoup
Tzuman
Je ne suis pas sûr d'avoir bien compris.
La méthode d'interpolation est assez simple en fait : il s'agit d'une interpolation linéaire entre deux points d'arrivée de l'image supérieure (c'est pourquoi j'ai dit plusieurs fois que les versions interpolées et non interpolées (la "méthode keris" classique) ont exactement le même nombre de points exacts garantis par barre d'image supérieure : 1 par barre d'image supérieure (le reste est une question de probabilité et de changements de prix). Vous pouvez laisser de côté le rafraîchissement des valeurs interpolées (ou "step-like"), (ne calculer que la barre actuelle du cadre temporel inférieur) mais vous obtiendrez alors un indicateur de repeinture classique (puisque l'état exact à un certain point du cadre temporel inférieur ne peut pas être calculé exactement dans de nombreux cas - cela nécessiterait un mode de calcul d'ingénierie d'inversion vraiment compliqué auquel je ne pense pas que metatrader "survivrait").
J'espère avoir bien compris la question et que la réponse est celle que vous attendiez.Bonjour Mladen et Tzuman,
J'ai également une question liée à ce problème depuis longtemps. Lorsque j'ai utilisé un certain type de MA (Ema ou LWMA, par exemple) de TF plus petit à Price_Close avec Period_Length réglé pour être équivalent à la longueur de la même MA pour TF plus élevé (EMA(H1-24 périodes) et EMA(H4-6 périodes) par exemple), ils ne sont pas les mêmes. Pouvez-vous m'expliquer cela ?
Bonjour Mladen et Tzuman, J'ai aussi une question liée à ce problème depuis longtemps. Lorsque j'ai utilisé un certain type de MA (Ema ou LWMA, par exemple) de TF plus petits à Price_Close avec Period_Length réglé pour être équivalent à la longueur de la même MA pour TF plus élevés (EMA(H1-24 périodes) et EMA(H4-6 périodes) par exemple), ils ne sont pas les mêmes. Pouvez-vous m'expliquer cela ?
fareastol
Multiplier la période pour obtenir des valeurs plus élevées pour les moyennes n'est pas une mauvaise méthode (parmi d'autres, Alexander Elder a utilisé cette méthode dans les premiers jours de TA) mais c'est simplement une approximation. La raison est simple : les ensembles de données utilisés pour calculer les moyennes sont différents et vous ne pouvez pas obtenir les mêmes résultats à partir de différents ensembles de données. A mon avis, il est préférable d'utiliser la MTF classique (comme nous l'utilisons), car certains indicateurs ne peuvent tout simplement pas être calculés de cette façon (juste un exemple : essayez le RSI, et la plupart sont comme ça).
A propos de la fonction adaptative.
Bonjour Mladen ,
J'ai bien étudié votre fonction adaptative de volativité, pourquoi ne pas utiliser la fonction mathématique ronde ?
Avec cela (si j'ai bien compris), votre période adaptative peut fonctionner avec tout type de moyenne mobile ou d'indicateurs !
Salutations.
A propos de la fonction adaptative.
Bonjour Mladen ,
J'ai bien étudié votre fonction adaptative de volativité, pourquoi ne pas utiliser la fonction mathématique ronde ?
Avec cela (si j'ai bien compris), votre période adaptative peut fonctionner avec tout type de moyenne mobile ou d'indicateurs !
Salutations.sohocool
Pour une raison simple : simplement pour certaines moyennes, lorsque vous changez la période de calcul, vous obtiendrez des moyennes "en escalier" (changement très soudain de la valeur) au lieu d'avoir des valeurs logiques, aussi lisses que possible pour ce type de moyenne.
C'est pourquoi j'ai dit à plusieurs reprises que seules les moyennes qui peuvent calculer des périodes fractionnaires peuvent être adaptées. Les autres peuvent être adaptées aussi (il n'y a pas de limite pour cela) mais le résultat lui-même n'est pas "agréable" (j'espère que vous comprenez ce que j'entends par "agréable"). D'un autre côté, les moyennes comme l'EMA par exemple, "héritent" de leur valeur précédente et utilisent cette valeur dans le calcul. Le calcul peut utiliser des périodes fractionnaires, ce qui le rend raisonnablement lisse et "logique" lorsque la période de calcul est modifiée en permanence.
_____________________________
A titre expérimental : essayez d'adapter la SMA (qui, de par sa nature, ne permet qu'une période de calcul intermédiaire) et vous verrez à quoi ressemblent les résultats dans certains cas.
sohocool
Pour une raison simple : simplement pour certaines moyennes, lorsque vous changez la période de calcul, vous obtenez des moyennes "en escalier" (changement très soudain de la valeur) au lieu d'avoir des valeurs logiques, aussi lisses que possible pour ce type de moyenne.
C'est pourquoi j'ai dit à plusieurs reprises que seules les moyennes qui peuvent calculer des périodes fractionnaires peuvent être adaptées. Les autres peuvent être adaptées aussi (il n'y a pas de limite pour cela) mais le résultat lui-même n'est pas "agréable" (j'espère que vous comprenez ce que j'entends par "agréable"). D'un autre côté, les moyennes comme l'EMA par exemple, "héritent" de leur valeur précédente et utilisent cette valeur dans le calcul. Le calcul peut utiliser des périodes fractionnaires, ce qui le rend raisonnablement lisse et "logique" lorsque la période de calcul est modifiée en permanence.
_____________________________
A titre expérimental : essayez d'adapter la SMA (qui, de par sa nature, ne permet que l'utilisation de l'interger pour le calcul de la période) et vous verrez à quoi ressemblent les résultats dans certains cas.Bonjour Mladen,
Merci beaucoup pour votre réponse rapide.
Oui, je sais que votre méthode est la meilleure.
Mais avec interger le pas sera un petit pas (moins de 1 période) autour de (14,4)=14.
et le marché n'est pas si logique
Bonjour Mladen,
Merci beaucoup pour votre réponse rapide.
Oui, je sais que votre méthode est la meilleure.
Mais avec interger le pas sera un petit pas (moins de 1 période) autour de (14,4)=14.
et le marché n'est pas si logiquesohocool
J'ai l'impression que vous oubliez que la période de calcul pour des barres consécutives ne sera pas toujours similaire. Par exemple : sur une barre, ce sera 14, mais sur une autre, ce sera 4. Et dans ce cas, il y aura un très grand changement. Si vous essayez d'adapter la SMA, vous verrez immédiatement ce qui se passe dans des cas comme celui-ci. Ce n'est donc pas seulement la partie fractionnaire (qui aide beaucoup à la maintenir "lisse"), mais le fait qu'elle puisse utiliser une période fractionnaire montre généralement que le calcul est adapté à l'adaptation (parce que dans la plupart des cas, lorsque la période peut être fractionnaire, la valeur précédente de la moyenne est utilisée sous une forme ou une autre dans le calcul et sans "héritage", il est presque impossible d'obtenir une moyenne d'apparence normale lors de l'adaptation).