Statistiques de dépendance entre guillemets (théorie de l'information, corrélation et autres méthodes de sélection de caractéristiques) - page 15
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Les gens qui ont EViews ne posent pas de telles questions, hee-hee
Auriez-vous l'amabilité de m'envoyer, en privé ou ici, EViews, si possible ?
.
Les personnes qui ont EViews ne posent pas ce genre de questions, heehee
Eh bien oui, c'est une question idiote, je suis d'accord. Les garanties sont les mêmes que pour le modèle lui-même.
Quelle version avez-vous ? Ils disent que la 5 est dépassée.
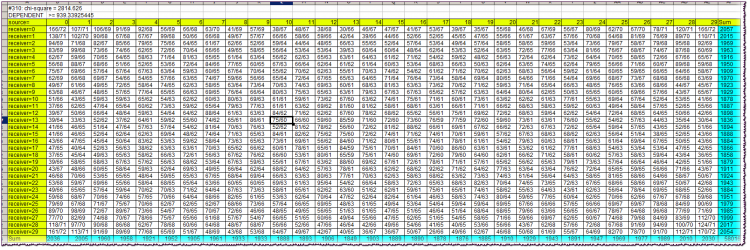
Première ligne du bloc : #310 : chi-carré = 2814.626Premièrement - la valeur de la variable Lag. Ensuite, la valeur du chi-deux de l'indépendance des variables.
Deuxième ligne : conclusion de dépendance/indexation, ainsi que la valeur limite du chi-deux.
Les cellules jaunes du tableau sont des bouchons. Ils vous permettent d'orienter les caractères de l'alphabet qui ont été observés simultanément à l'intersection de la ligne et de la colonne correspondantes. Rappelons que les alphabets à la source et au récepteur sont identiques et égaux aux quantiles dans lesquels se situent les rendements des barres correspondantes (source et récepteur).
Par exemple, à l'intersection de la colonne source=10 et de la ligne récepteur=13, nous trouvons une valeur de cellule de 75/60. Cela signifie que la combinaison "le rendement de la source (barre dans le passé) pris dans le 10e quantile et le rendement du récepteur (barre plus proche du présent) pris dans le 13e quantile" a été observée 75 fois dans l'historique, le nombre théorique de ces combinaisons étant de 60 si elles étaient indépendantes.
Les cellules turquoises sont les sommes des fréquences réelles par ligne ou par colonne nécessaires au calcul du chi carré.
Le chi carré lui-même dans le cas de l'indépendance de la source et du récepteur devrait presque toujours être plus petit que celui de la limite, c'est-à-dire spécifié dans la deuxième ligne du bloc. Comme on peut le voir, il est beaucoup plus grand, presque 3 fois plus grand. Cela indique une très forte dépendance à la barre dans ce cas.
Le fichier entier, même archivé, prend trop de place, je ne peux donc pas le poster ici.
Eh bien oui, c'est une question idiote, je suis d'accord. Les garanties sont les mêmes que pour le modèle lui-même.
Quelle version utilisez-vous ? Ils disent que la 5 est dépassée.
Il existe la définition de l'entropie de Shannon, dans laquelle l'indépendance est obligatoire.
Il existe également une définition de l'information mutuelle, dans laquelle la définition de Shannon est appliquée de manière purement formelle, puisqu'on suppose toujours que des dépendances existent.
Si vous voulez creuser dans les profondeurs philosophiques et les contradictions de la définition de l'information mutuelle - je vous en prie, creusez. Je préfère ne pas m'en soucier et me contenter d'utiliser la formule "américaine" avec des probabilités, sans me soucier de l'indépendance.
C'est un peu un terme inapproprié. La traduction des significations de l'écorce..., TI est la suivante. Il existe un concept d'entropie. Il faut bien comprendre que derrière ce mot étranger, beau et incompréhensible, se cache une figure inventée artificiellement. Dans les manuels, ceux qui sont plus honnêtes, il est écrit directement ainsi, une mesure d'incertitude introduite de manière axiomatique. Il s'agit en fait d'une convolution. En gros, un grand tableau décrivant les états et leurs fréquences, à l'aide de formules arithmétiques, est convolué en un seul nombre. De plus, seules les fréquences sont cumulées, et les états eux-mêmes (qui, soit dit en passant, peuvent aussi avoir leurs mesures) ne sont intéressants que du point de vue de leur nombre total.
Dans ter.faith il y a une opération similaire, grosso modo, les systèmes mo sont comptés de manière similaire. Mais c'est seulement là que les probabilités des états sont multipliées par leurs mesures, additionnées et que l'on obtient un chiffre, sur lequel sont ensuite prouvés les théorèmes de convergence, etc. Ici, ce n'est pas le cas. Ici, la fréquence elle-même (appelée sa probabilité), ou plutôt son logarithme, fait office de mesure. Le logarithme résout certains problèmes arithmétiques que Shannon a formulés en trois conditions (doit croître de façon monotone, etc.).
Après cela, Shannon dit : "Mes amis, vous savez, j'ai trouvé des règles raisonnables et évidentes pour additionner les nombres que j'ai récemment découverts, que j'appelle entropie, à partir de deux tablettes différentes. Des amis (surtout des militaires) me demandent : - Bien, comment faites-vous ? - Très simplement. - Shannon leur répond en faisant des yeux doux. - Disons qu'une plaque n'est pas reliée à une autre, elles sont indépendantes, cela arrive dans la vie. Et dans ce cas, j'ai un théorème sur l'addition des entropies, avec un résultat merveilleux - les chiffres s'additionnent tout simplement ! - Bien, mais si les plaques sont connectées d'une manière incompréhensible ? - Ici, c'est aussi simple que cela : construire un grand tableau carré à partir des deux tableaux originaux, multiplier les probabilités dans chaque cellule. Nous additionnons les nombres dans les cellules par colonnes, additionnons les colonnes séparément, construisons un nouveau tableau, divisons l'un par l'autre, ici tôt zéro, ici poisson emballé... Oups, le résultat est un seul nombre, que j'appelle entropie conditionnelle ! Ce qui est intéressant, c'est que l'entropie conditionnelle peut être calculée aussi bien du premier tableau au second, et vice versa ! Et pour tenir compte de cette malheureuse dualité, j'ai inventé l'entropie mutuelle totale, et c'est le même chiffre ! - Et donc, - demandent les amis, en grignotant du pop-corn, - Il est beaucoup plus facile de comparer un chiffre avec un autre, que de comprendre l'essence des données à partir des tableaux originaux. Et c'est encore plus facile lorsqu'il s'agit de comprendre le sens et la fiabilité des relations - c'est ennuyeux, vraiment. Rideau.
Voilà à quoi ressemble pour moi une brève histoire de TI. Compilé à partir de mes propres recherches et des affirmations d'un dictionnaire universitaire (voir les citations précédentes).
Maintenant, ce qui est important. Le point clé de toute cette histoire est caché dans l'entropie conditionnelle. En fait, si l'on veut opérer avec un chiffre, il n'est pas nécessaire de compter les informations mutuelles et autres, il suffit de maîtriser la technique de calcul de l'entropie conditionnelle. C'est elle qui donnera une certaine mesure de l'interrelation de l'un avec l'autre. Il est donc nécessaire de comprendre que les chiffres des tableaux doivent être "fixes" et que les relations entre les tableaux doivent être "fixes". En outre, les chiffres initiaux des tableaux doivent provenir de sources appropriées.
Il faut dire qu'il existe des extensions de TI au cas des chaînes de Markov. On dirait que c'est juste ce que le docteur a ordonné. Mais non, les probabilités de transition pour le marché ne sont pas constantes, en raison de la non-stationnarité générale. En outre, si pour le CM, la façon dont le système a abouti à son état actuel n'a pas d'importance, pour le marché, c'est très important.
Je ne sais pas quel est l'alphabet de votre problème. J'ai un système composé d'une paire de barres séparées par la distance Lag. Un bar, dans le passé, est la source et l'autre est le récepteur. Les alphabets des deux sont identiques (en ce qui concerne les retours de barre, bien sûr).
En clair, quelque chose de similaire à l'autocorrélation, mais avec une mesure différente. Mes objections sont exactement les mêmes que pour le cas du CM. Et tous les autres, la stationnarité, etc.
SZU. Je dois dire que si vous le négociez vraiment (TI) et avec succès, ce qui avec elle, avec des objections. Laissez même un pied de lièvre sur le moniteur, si ça peut aider.
Lisez HideYourRichess.
Oui, intéressant. En effet, la matrice de fréquence des états conditionnels d'un système - sous l'hypothèse de connectivité - étant reformulée en termes d'entropie conditionnelle, nous donne UN chiffre décrivant la possibilité qu'il existe une certaine déterminabilité d'une variable par rapport à une autre. Si la PDF d'une telle matrice initiale est uniforme, alors nous avons l'entropie maximale du système (bien sûr, je voulais dire l'entropie conditionnelle). Et s'il y a des irrégularités, l'entropie sera moindre. En première approximation, nous pouvons nous contenter d'un seul chiffre. Vous avez raison. Et l'information mutuelle pour un ensemble de variables, séparées du récepteur par Lag, comme l'a écrit Alexey, est calculée déjà dans un but très concret, à savoir pour la sélection de variables informatives.
Pour l'instant, je n'utilise pas TI. Ce sujet était un "premier essai", je pense ensuite.
HideYourRichess: Вот так выглядит краткая история ТИ в моём исполнении. Составлена по мотивам моих собственных изысканий и утверждений академического словарика (см. цитаты ранее).
Très intéressant. Shannon a fait un tel bazar que nous sommes encore en train de le résoudre...
Il faut dire qu'il existe des extensions de TI pour les cas de chaînes de Markov. On dirait que c'est juste ce que le docteur a ordonné. Mais non, les probabilités de transition pour le marché ne sont pas constantes, en raison de la non-stationnarité générale. En outre, si pour le CM il importe peu de savoir comment le système s'est avéré dans l'état actuel, pour le marché, c'est très important.
Justement, le flux de retour n'est pas un processus markovien, car le retour de la barre zéro dépend fortement du retour non seulement de la première barre, mais aussi de la deuxième, de la troisième, etc. En tout cas, c'est ainsi que l'on peut interpréter directement l'étude de la branche principale.
ZS. Je dois dire que si vous faites vraiment ce commerce (TI) et avec succès, alors que diable, avec des objections. Laissez le lièvre poser sa patte sur le moniteur, si ça peut aider.
Non, je ne le fais pas. Mais il serait très intéressant de le développer en quelque chose de commercial. J'ai entendu dire par alsu (Alexey a disparu quelque part, désolé), qu'il se souvient vaguement d'une émission sur la chaîne RBC, dans laquelle apparaissait un trader rhétoricien qui négociait vraiment quelque chose de similaire. Et il a parié beaucoup d'argent dessus. Et il appelle son système "attraper les inefficiences du marché".
Je pense à l'entropie depuis longtemps maintenant. J'ai même mis quelque chose ici. Mais alors, il s'agissait plutôt d'entropie en physique statistique, et non de TI, et faisait référence à la multidevise. Quoi qu'il en soit, le karma me murmure quelque chose d'entropique à l'oreille depuis quelques années, et je l'écoute en essayant de comprendre ce qu'il attend de moi...
Justement, le flux de retour n'est pas un processus markovien, car le retour de la barre zéro dépend fortement du retour non seulement de la première barre, mais aussi de la deuxième, de la troisième, etc. En tout cas, c'est ainsi que l'on peut interpréter directement l'étude de la branche principale.
Non, je ne fais pas de commerce. Mais il serait très intéressant d'en faire quelque chose d'échangeable. J'ai entendu dire par alsu (Alexey a disparu quelque part, désolé), qu'il se souvient vaguement d'une émission sur la chaîne RBC, dans laquelle apparaissait un trader rhétoricien qui négociait réellement quelque chose de similaire. Et il a parié beaucoup d'argent dessus. Et il appelle son système "attraper les inefficiences du marché".
Et ça fait longtemps que je pense aux entropies. Et j'ai même posté quelque chose ici. Mais à l'époque, cela ressemblait davantage à l'entropie de la physique statistique, et non à TI, et était lié à la multidevise. Quoi qu'il en soit, le karma me chuchote quelque chose d'entropique à l'oreille depuis quelques années maintenant, et je l'écoute en essayant de comprendre ce qu'il attend de moi...
Très intéressant.
Mais pourriez-vous, Alexey, formuler plus clairement (sur votre tableau) à quelle hypothèse sur la distribution des rendements correspondent les estimations du chi-deux ?
Le "browne" primordial, ou quelque chose de plus cool ?
;)