Qu'est-ce que le calcul des différences ?
Elle l'est :
Δf(xk) = f (xk+1) - f (xk)
Je propose de rassembler les indicateurs et les experts du calcul des différences dans ce fil, en code source ouvert.
J'ai réécrit l'indicateur dans une version plus claire pour vous donner un exemple :
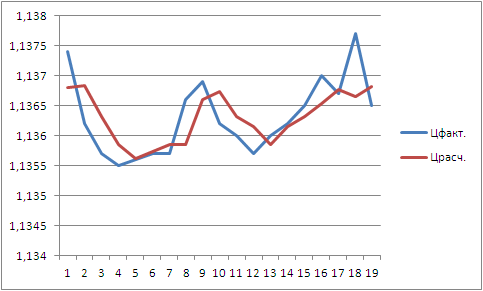
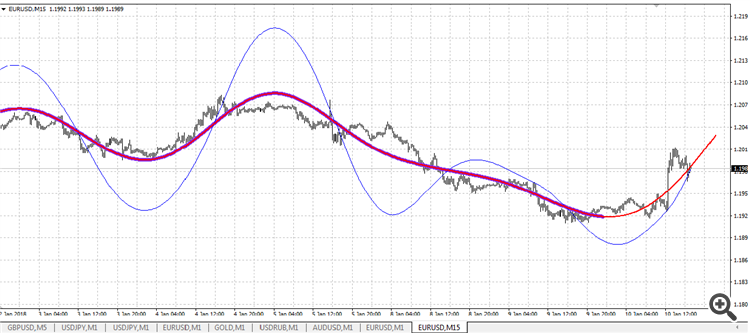
Sur le graphique, ça ressemble à ça :
La ligne bleu-rouge est une interpolation (trouver un point à l'intérieur de l'intervalle) par un polynôme de 4ème degré avec un levier de 72.
a1_Buffer[i]=((open[i] - Znach) +5061600*a1_Buffer[i+1 ]-7489800 *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975;
La ligne bleue fine est l'extrapolation (trouver un point en dehors de l'intervalle) par le polynôme de degré 2 avec un levier 78.
a2_Buffer[i]= 3160*a1_Buffer[i] -6240 *a1_Buffer[i+1 ] + 3081*a1_Buffer[i+2 ];
La ligne rouge est la ligne de construction du polynôme de puissance 4. Il est redessiné et basé sur le point d'ouverture de la dernière barre.
a4_Buffer[i+92]=a1_Buffer[i]; if(i<=10) { for(z=92-1;z>=0;z--){ a4_Buffer[i+0+z]= 5*a4_Buffer[i+1+z] - 10*a4_Buffer[i+2+z] + 10*a4_Buffer[i+3+z] - 5*a4_Buffer[i+4+z] + 1*a4_Buffer[i+5+z]; }}
Qu'est-ce que le calcul des différences ?
Elle l'est :
Δf(xk) = f (xk+1) - f (xk)
Oui.
Il est directement lié au binôme de Newton.
C'est vrai pour les points équidistants :
1*Y1-2*Y2+1*Y3=0 est l'équation de différence d'une ligne droite.
1*Y1-3*Y2+3*Y3-1*Y4=0 - l'équation différentielle de la parabole du second degré.
1*Y1-4*Y2+6*Y3-4*Y4+ 1*Y5=0 - équation différentielle de la parabole du troisième degré.
Il se recoupe également avec les sujets :
https://www.mql5.com/ru/forum/61389/page48#comment_5633264
https://www.mql5.com/ru/forum/211220/page2#comment_5632736 .

- 2017.07.20
- www.mql5.com
Oui.
C'est ce que tout le monde a fait... l'écriture...
L'avenir dépend-il du passé ?
C'est ce que tout le monde a fait... l'écriture...
L'avenir dépend-il du passé ?
Pour chaque action, il y a une trace dans le présent, qui affecte bien sûr le futur. :))))
Je suggère de ne pas parler de philosophie dans ce fil de discussion, mais uniquement de mathématiques, de programmation, de tests et d'optimisation.
Oui.
Directement lié au binôme de Newton.
Pour des points équidistants, c'est vrai :
Y1-2*Y2+Y3=0 - équation de différence d'une ligne droite.
Y1-3*Y2+3*Y3-Y4 =0 - l'équation différentielle de la parabole du second degré.
Y1-4*Y2+6*Y3-4*Y4 + Y5 =0 - est l'équation différentielle de la parabole du troisième degré.
Avez-vous essayé cette formule ?
Y = a0 + a1X + a2X^2 + a3X^3 + a4X^4
où :
X est le prix de la barre précédente ;
Y - prix de la barre actuelle.
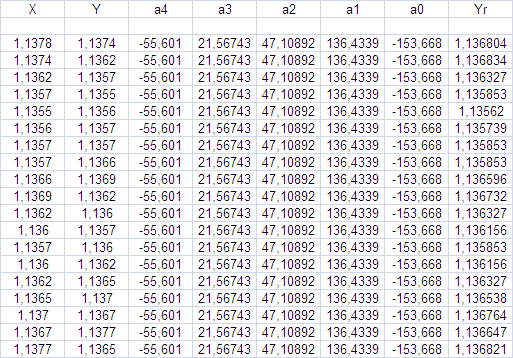
Et nous obtenons ainsi l'image suivante :
Avez-vous essayé cette formule ?
Y = a + bX + cX^2 + dX^3 + eX^4
Bien sûr, dans cette forme il y a X et Y, alors que dans l'équation de récurrence, seul Y et tous les coefficients (a + bX+ cX^2+ dX^3+ eX^4) sont réduits et remplacés par cinq valeurs de Y lui-même.
J'ai regardé le code, est-ce que j'ai bien compris, c'est une variante d'un filtre à rétroaction ? D'où viennent les coefficients 5061600, 4926624 et autres ?
En fait, d'où vient l'indé, d'Internet ? ))
1. J'ai regardé le code, est-ce que j'ai bien compris, c'est une variante d'un filtre à rétroaction ?
2. et d'où viennent les coefficients 5061600, 4926624 et autres ?
3. En général, d'où vient l'inducteur, d'internet ? ))
1. Oui. Ce filtre est vieux de 400 ans avec seulement une histoire écrite : Descartes, Newton, Pascal, Taylor, Lagrange.
2. Les coefficients sont calculés. Il semble qu'en deuxième année, nous nous soyons familiarisés avec les méthodes de Lagrange et de Taylor. Il semble y avoir beaucoup de variantes pour le calcul des coefficients.
3. Celui-ci en particulier a été dessiné aujourd'hui. :)))))
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
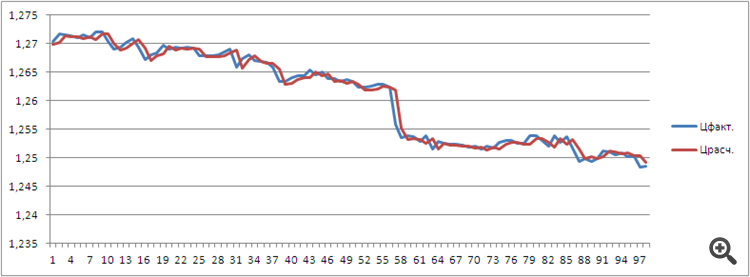
Je propose de rassembler les indicateurs et les experts du calcul des différences dans ce fil, en code source ouvert.
Si l'intérêt est là, nous finirons par construire ou dessiner quelque chose d'utile. :)
J'ai réécrit l'indicateur dans une version plus claire à titre d'exemple :