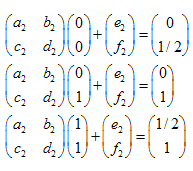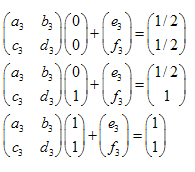Création de fractales dans MQL5 à l'aide des Systèmes de Fonctions Itérées (Iterated Function Systems - IFS) - expert pour MetaTrader 5

Introduction

Il existe de nombreux programmes, permettant la création d'ensembles auto-similaires, définis par des Systèmes de Fonctions Itérées (IFS). Voir, par exemple, Fractint, Fractal Designer ou IFS Matlab Generator. Grâce à la rapidité du langage MQL5 et à la possibilité de travailler avec des objets graphiques, ces beaux ensembles peuvent être étudiés dans le terminal client MetaTrader 5.

La bibliothèque cIntBMP, développée par Dmitry (Integer) offre de nouvelles possibilités graphiques et simplifie grandement la création d'images graphiques. Cette bibliothèque a été récompensée par un prix spécial par MetaQuotes Software Corp.

Dans cette publication, nous examinerons les exemples de travail avec la bibliothèque cIntBMP. De plus, nous couvrirons les algorithmes de création d'ensembles fractals utilisant les systèmes de fonctions itérées.

1. Transformation Affine du Plan

La transformation affine de plan est une application . Généralement, la transformation 2D affine peut être définie avec une matrice et un vecteur . Le point de coordonnées (x,y) se transforme en un autre point en utilisant la transformation linéaire :

La transformation doit être non singulière, le . La transformation affine modifie la taille fois.

Les transformées affines ne changent pas la structure des objets géométriques (les lignes transformées en lignes), l'AT permet de décrire de simples "déformations" des objets, telles que la rotation, la mise à l'échelle et la translation.

Exemple de transformées planes affines :

1) Rotation du plan sur l'angle  :

2) "Mise à l'échelle" d'un plan avec les coefficients et (axes X et Y) :

3) Translation du plan par  vecteur :

Les cartographies de contraction sont la clé (voir les résultats de Hutchinson).

Si et ont des coordonnées et et est une métrique (par exemple, métrique d'Euclide : ). La transformation affine appelée contraction si , où .

Voici un exemple de transformation affine :

Le résultat est:

2. Transformations de Similarité

Les fractales sont construites de la manière suivante : un objet géométrique (simple) (section, triangle, carré) divisé en N pièces et M d'entre elles utilisées pour la "construction" ultérieure de l'ensemble (si N=M, nous obtiendrons la dimension entière de l'ensemble résultant). De plus, ce processus s'est répété encore et encore pour chacune des pièces.

Fractales classiques :

Sections :

• Courbe triadique de Koch, N=3, M=4 ;
• Poussière de Chantre, N=3, M=2 ;

Triangle :

• Joint Sierpinski, N=4, M=3 ;

Carrés :

• Tapis de Sierpinski, N=9, M=8;
• Fractale de Vichek, N=9, M=5.
  

etc.

Les fractales ont une structure auto-similaire, certaines d'entre elles peuvent être définies par plusieurs transformations de similarité. La structure de la transformée affine dépend du mode de construction fractale.

Comme vous le verrez plus loin, c'est très simple, et le seul problème que nous avons à résoudre est de ne décrire que la première itération de la construction fractale et de trouver l'ensemble correspondant de transformées affines.

Supposons que nous ayons un ensemble. Selon l'algorithme de création fractale, nous devons le réduire, le faire pivoter et le "mettre à un certain endroit". Le problème est de décrire ce processus à l'aide de transformations affines, c'est-à-dire qu'il faut trouver la matrice et le vecteur.

Il est facile de prouver qu'il suffit de prendre 3 points de l'ensemble initial (non trivial) et de les transformer en 3 points correspondants de l'ensemble "réduit". Cette transformation conduira à 6 équations linéaires, nous permettant de trouver les a,b,c,d,e,f comme solution.

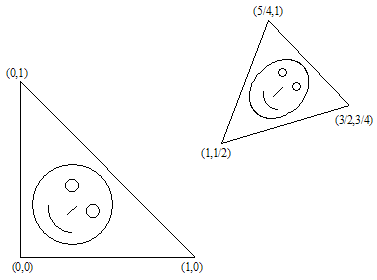
Montrons-le. Supposons que le triangle soit transformé en triangle .

En résolvant le système d'équations linéaires nous pourrons obtenir les coefficients a,b,c,d,e et f :

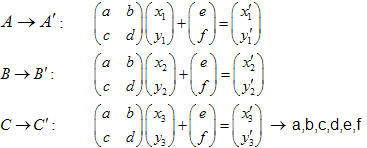
Exemple : Joint Sierpinski :

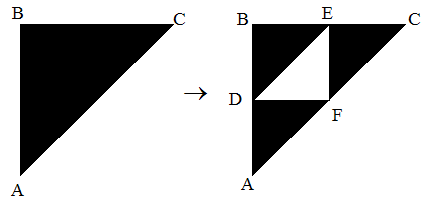
Les coordonnées des points sont :

• A (0,0)
• B (0,1)
• C (1,1)
• D(0,1/2)
• E (1/2,1)
• F(1/2,1/2)
  

Nous avons 3 transformations :

1. ABC -> ADF
2. ABC -> DBE
3. ABC -> FEC
   

Le système d'équations linéaires se présente comme suit :

1. 
   
2. 
   
3. 
   

Les solutions sont : , ,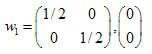

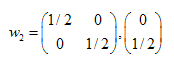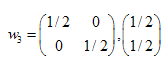
Nous avons trouvé les coefficients de trois transformées affines. De plus, nous les utiliserons pour créer des ensembles auto-similaires.

3. Création de fractales à l'aide des Systèmes de Fonctions Itérées

Le Système de Fonctions Itérées (IFS) est un ensemble de contractions affines où - est les "pondérations". Chacune des fonctions IFS est définie par 7 nombres : , où les poids sont utilisés lors du processus d'itération comme une probabilité de n-ième transformation. Il est préférable de définir leurs valeurs, proportionnelles à la contraction : .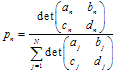

Considérons l'algorithme de construction fractale utilisant le système de fonctions itérées (voir aussi Chaos Game).

Le premier dont nous avons besoin est de prendre un point initial avec des coordonnées . Ensuite, nous choisissons au hasard certaines des contractions et traçons le point . Et encore une fois, choisissons au hasard une des contractions et traçons . Enfin, nous aurons le comme un ensemble de points.

Le choix de la contraction dépend de sa "probabilité". Si nous répétons le processus (par exemple, jusqu'à ~30 000 points) et traçons l'ensemble résultant, nous verrons sa structure malgré le processus aléatoire.

Voici un exemple de joint Sierpinski :

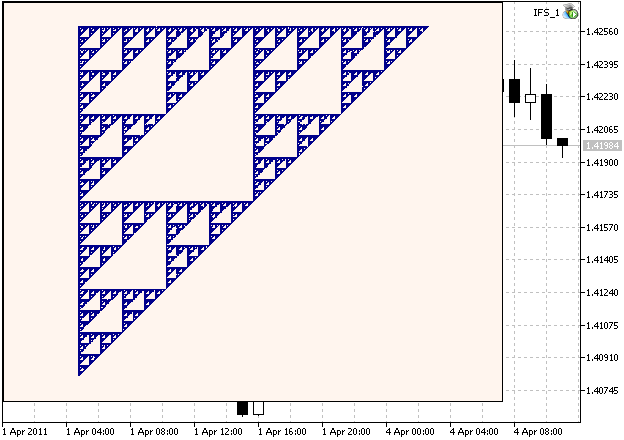
Figure 1. Le Sierpinski Gasket, généré avec les coefficients IFS calculés au chapitre 2

Le code :

//+------------------------------------------------------------------+
//|                                        IFS_Sierpinski_Gasket.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

//-- inclut le fichier avec la classe cIntBMP
#include <cIntBMP.mqh>

//-- Coefficients IFS de Sierpinski Gasket
//-- matrices (a,b,c,d)
double IFS_a[3] = {0.50,  0.50,  0.50};
double IFS_b[3] = {0.00,  0.00,  0.00};
double IFS_c[3] = {0.00,  0.00,  0.00};
double IFS_d[3] = {0.50,  0.50,  0.50};
//-- vecteurs (e,f)
double IFS_e[3] = {0.00,  0.00,  0.50};
double IFS_f[3] = {0.00,  0.50,  0.50};
//-- "probabilités" de transformations, multipliées par 1000
double IFS_p[3]={333,333,333};

double Probs[3]; // Tableau Probs - utilisé pour choisir les transformations IFS
cIntBMP bmp;     // instance de la classe cIntBMP
int scale=350;  // coefficient d'échelle
//+------------------------------------------------------------------+
//| Fonction d'initialisation de l'Expert                            |
//+------------------------------------------------------------------+
int OnInit()
  {
//-- Prépare le tableau Probs
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
//-- taille de l'image BMP
   int XSize=500;
   int YSize=400;
//--  crée une image bmp XSizexYSize avec la couleur de fond clrSeashell
   bmp.Create(XSize,YSize,clrSeashell);
//-- image rectangle
   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

//-- coordonnées du point (seront utilisées dans la construction de l'ensemble)
   double x0=0;
   double y0=0;
   double x,y;
//-- nombre de points à calculer (plus de points - image détaillée)
   int points=1500000;
//-- calculde l'ensemble
   for(int i=0; i<points; i++)
     {
      // choisit la transformation IFS avec probabilités, proportionnelles à celles définies
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            // transformation affine
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            // met à jour les coordonnées précédentes
            x0 = x;
            y0 = y;
            // convertit en coordonnées d'image BMP
            // (notez l'axe Y dans cIntBMP)
            int scX = int (MathRound(XSize/2 + (x-0.5)*scale));
            int scY = int (MathRound(YSize/2 + (y-0.5)*scale));
            // si les coordonnées du point sont à l'intérieur de l'image, dessine le point
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); }
            break;
           }
        }
     }
//-- enregistre l'image dans un fichier
   bmp.Save("bmpimg",true);
//-- trace l'image sur le graphique
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Fonction de désinitialisation de l'Expert                        |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- efface le graphique
   ObjectDelete(0,"IFS");
//--- supprime le fichier
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------+

Si nous définissons l'échelle sur 1 350, augmentons le nombre d'itérations à 1 500 000 et modifions le décalage du point initial :

int scX = MathRound(XSize/2 + (x-0.75)*scale);
int scY = MathRound(YSize/2 + (y-0.75)*scale);

nous pourrons voir la région agrandie de l'ensemble. On peut voir (Fig. 2), qu'il a une structure auto-similaire :

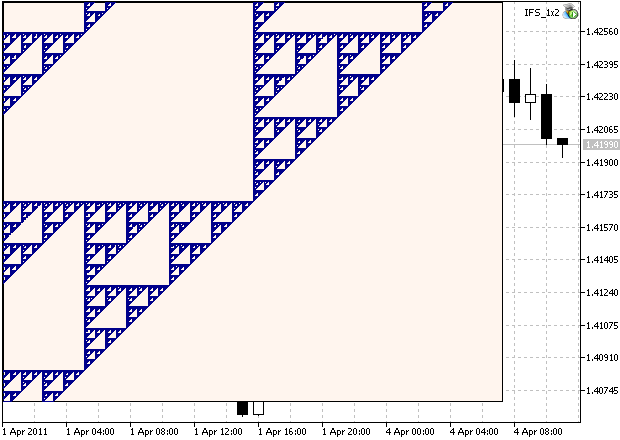
Figure 2. Région agrandie du joint Sierpinski

Considérons la fameuse Fougère de Barnsley, proposée par Michael Barnsley. C'est plus complexe.

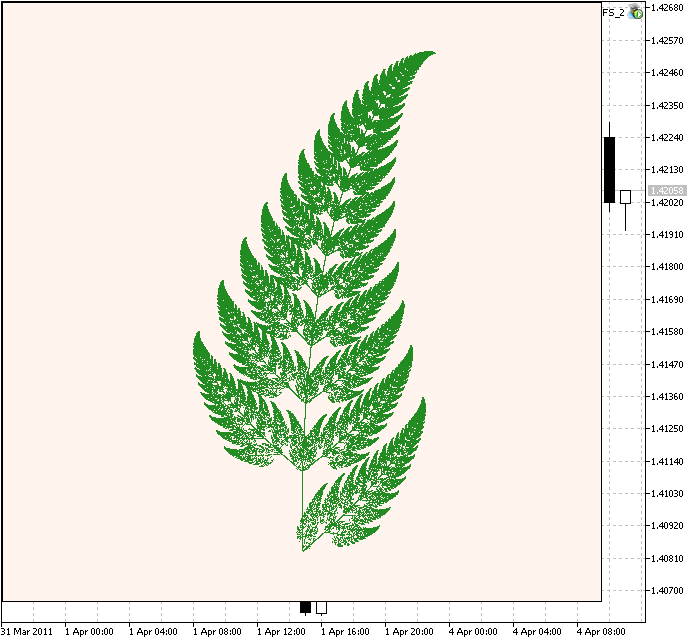
Figure 3. Fougère de Barnsley

Le code est similaire, mais dans ce cas nous avons 4 contractions IFS avec des poids différents.

//+------------------------------------------------------------------+
//|                                                     IFS_fern.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <cIntBMP.mqh>
//-- Coefficients IFS de la Fougère de Barnsley
//-- matrices (a,b,c,d) 
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
//--vecteurs  (e,f) 
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
//-- "probabilités" de transformations, multipliées par 1000
double IFS_p[4] = {10,     850,    70,     70};

double Probs[4];
cIntBMP bmp;
int scale=50;
//+------------------------------------------------------------------+
//| Fonction d'initisation de l'Expert                               |
//+------------------------------------------------------------------+
int OnInit()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }

   int XSize=600;
   int YSize=600;

   bmp.Create(XSize,YSize,clrSeashell);

   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

   double x0=0;
   double y0=0;
   double x,y;

   int points=250000;

   for(int i=0; i<points; i++)
     {
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            x0 = x;
            y0 = y;
            int scX = int (MathRound(XSize/2 + (x)*scale));
            int scY = int (MathRound(YSize/2 + (y-5)*scale));
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrForestGreen); }
            break;
           }
        }
     }
   bmp.Save("bmpimg",true);
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Fonction de désinitialisation de l'Expert                        |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ObjectDelete(0,"IFS");
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------+ 

Il est remarquable qu'une structure aussi complexe puisse être définie par seulement 28 chiffres.

Si nous augmentons l'échelle à 150 et définissons les itérations sur 1250000, nous verrons le fragment zoomé :

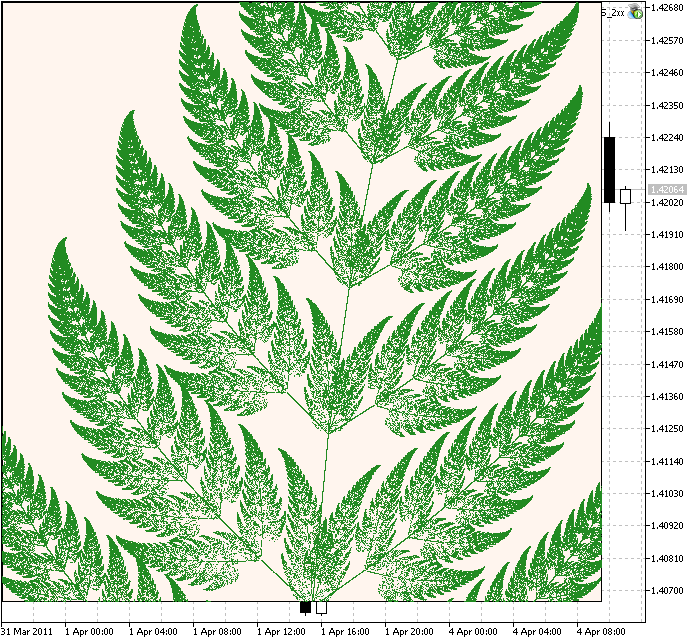
Figure 4. Un fragment de la Fougère de Barnsley

Comme vous le voyez, l'algorithme est universel, il vous permet de générer différents ensembles de fractales.

L'exemple suivant est Sierpinski Carpet, défini par les coefficients IFS suivants :

//-- Coefficients IFS du joint Sierpinski
double IFS_a[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333};
double IFS_b[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_c[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_d[8] = {0.333, 0.333,  0.333,  0.333, 0.333,  0.333,  0.333, 0.333};
double IFS_e[8] = {-0.125, -3.375, -3.375,  3.125, 3.125, -3.375, -0.125, 3.125};
double IFS_f[8] = {6.75, 0.25, 6.75,  0.25, 6.75, 3.5, 0.25, 3.50};
//-- "probabilités", multipliées par 1000
double IFS_p[8]={125,125,125,125,125,125,125,125};

Figure 5. Tapis Sierpinski

Dans le chapitre 2 nous avons considéré l'algorithme de calcul des coefficients des contractions IFS.

Considérons comment créer les "mots fractals". En russe, le mot "Fractales" ressemble à :

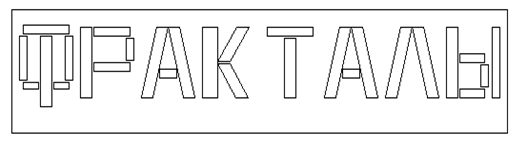
Figure 6. Mot "Fractales" en russe

Pour trouver les coefficients IFS, nous devons résoudre les systèmes linéaires correspondants. Les solutions sont :

//-- Coefficients IFS du mot "Fractales" en russe
double IFS_a[28]=
  {
   0.00, 0.03,  0.00, 0.09, 0.00, 0.03, -0.00, 0.07, 0.00, 0.07, 0.03,  0.03,  0.03,  0.00,
   0.04, 0.04, -0.00, 0.09, 0.03, 0.03,  0.03, 0.03, 0.03, 0.00, 0.05, -0.00,  0.05,  0.00
  };

double IFS_b[28]=
  {
   -0.11, 0.00, 0.07, 0.00, -0.07, 0.00, -0.11,  0.00, -0.07,  0.00, -0.11,  0.11, 0.00, -0.14,
   -0.12, 0.12,-0.11, 0.00, -0.11, 0.11,  0.00, -0.11,  0.11, -0.11,  0.00, -0.07, 0.00, -0.07
  };

double IFS_c[28]=
  {
   0.12,  0.00,  0.08,  -0.00,  0.08,  0.00,  0.12,  0.00,  0.04,  0.00,  0.12,  -0.12, 0.00,  0.12,
   0.06,  -0.06,  0.10,  0.00,  0.12,  -0.12,  0.00,  0.12,  -0.12,  0.12, 0.00,  0.04,  0.00,  0.12
  };

double IFS_d[28]=
  {
   0.00,  0.05,  0.00,  0.07,  0.00,  0.05,  0.00,  0.07,  0.00,  0.07,  0.00,  0.00,  0.07,  0.00,
   0.00,  0.00,  0.00,  0.07,  0.00,  0.00,  0.07,  0.00,  0.00,  0.00,  0.07,  0.00,  0.07,  0.00
  };

double IFS_e[28]=
  {
   -4.58,  -5.06, -5.16, -4.70, -4.09, -4.35, -3.73, -3.26, -2.76,  -3.26, -2.22, -1.86, -2.04, -0.98,
   -0.46,  -0.76,  0.76,  0.63,  1.78,  2.14,  1.96,  3.11,  3.47,  4.27,  4.60,  4.98,   4.60, 5.24
  };

double IFS_f[28]=
  {
   1.26,  0.89,  1.52,  2.00,  1.52,  0.89,  1.43,  1.96,  1.69,  1.24,  1.43,  1.41,  1.11,  1.43,
   1.79,  1.05,  1.32,  1.96,  1.43,  1.41,  1.11,  1.43,  1.41,  1.43,  1.42,  1.16,  0.71,  1.43
  };

//-- "probabilités", multipliées par 1000
double IFS_p[28]=
  {
   35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  
   35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35
  };

En conséquence, nous obtiendrons l'image suivante :

Figure 7. Mot auto-similaire

Le code source complet se trouve dans ifs_fractals.mq5.

Si nous agrandissons l'ensemble, nous voyons la structure auto-similaire :

Figure 8. Région agrandie de l'ensemble

Les ensembles auto-similaires, basés sur IFS, peuvent être construits à l'aide du Fractal Designer.

Nous avons couvert le sujet de la création d'ensembles fractals à l'aide des systèmes de fonctions itérées. Grâce à la bibliothèque cIntBMP, le processus est très simple. Il est maintenant temps de créer une classe et d'ajouter quelques fonctionnalités pour améliorer les images.

Vous remarquerez peut-être que la construction correcte des ensembles est guidée par les probabilités. La différence de probabilités signifie que l'ensemble a une structure irrégulière (voir les poids de l'IFS de la Fougère de Barnsley). Ce fait peut être utilisé pour la création de belles images. Nous devons définir la couleur, proportionnelle à la fréquence du point dans un quartier.

Cela peut être fait en utilisant l'écran virtuel (juste un tableau), si la couleur des pixels dépendra des valeurs précédentes. Enfin, l'écran virtuel sera rendu dans le bmp à l'aide de la Palette. L'image bmp elle-même peut être dessinée comme image d'arrière-plan du graphique.

Voici le code d'Expert Advisor, basé sur la classe CIFS :

//+------------------------------------------------------------------+
//|                                               IFS_Fern_color.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#include <cIntBMP.mqh>
//-- Coefficients IFS de la Fougère de Barnsley
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
double IFS_p[4] = {10,     850,    70,     70};
//-- Palette
uchar Palette[23*3]=
  {
   0x00,0x00,0x00,0x02,0x0A,0x06,0x03,0x11,0x0A,0x0B,0x1E,0x0F,0x0C,0x4C,0x2C,0x1C,0x50,0x28,
   0x2C,0x54,0x24,0x3C,0x58,0x20,0x4C,0x5C,0x1C,0x70,0x98,0x6C,0x38,0xBC,0xB0,0x28,0xCC,0xC8,
   0x4C,0xB0,0x98,0x5C,0xA4,0x84,0xBC,0x68,0x14,0xA8,0x74,0x28,0x84,0x8C,0x54,0x94,0x80,0x40,
   0x87,0x87,0x87,0x9F,0x9F,0x9F,0xC7,0xC7,0xC7,0xDF,0xDF,0xDF,0xFC,0xFC,0xFC
  };
//+------------------------------------------------------------------+
//| Classe CIFS                                                      |
//+------------------------------------------------------------------+
class CIFS
  {
protected:
   cIntBMP           m_bmp;
   int               m_xsize;
   int               m_ysize;
   uchar             m_virtual_screen[];
   double            m_scale;
   double            m_probs[8];

public:
                    ~CIFS()                          { m_bmp.Delete("bmpimg",true); };
   void              Create(int x_size,int y_size,uchar col);
   void              Render(double scale,bool back);
   void              ShowBMP(bool back);
protected:
   void              VS_Prepare(int x_size,int y_size,uchar col);
   void              VS_Fill(uchar col);
   void              VS_PutPixel(int px,int py,uchar col);
   uchar             VS_GetPixel(int px,int py);
   int               GetPalColor(uchar index);
   int               RGB256(int r,int g,int b) const {return(r+256*g+65536*b);      }
   void              PrepareProbabilities();
   void              RenderIFSToVirtualScreen();
   void              VirtualScreenToBMP();
  };
//+------------------------------------------------------------------+
//| Méthode Create                                                   |
//+------------------------------------------------------------------+
void CIFS::Create(int x_size,int y_size,uchar col)
  {
   m_bmp.Create(x_size,y_size,col);
   VS_Prepare(x_size,y_size,col);
   PrepareProbabilities();
  }
//+------------------------------------------------------------------+
//| Prépare l'écran virtuel                                          |
//+------------------------------------------------------------------+
void CIFS::VS_Prepare(int x_size,int y_size,uchar col)
  {
   m_xsize=x_size;
   m_ysize=y_size;
   ArrayResize(m_virtual_screen,m_xsize*m_ysize);
   VS_Fill(col);
  }
//+------------------------------------------------------------------+
//| Remplit l'écran virtuel avec la couleur spécifiée                |
//+------------------------------------------------------------------+
void CIFS::VS_Fill(uchar col)
  {
   for(int i=0; i<m_xsize*m_ysize; i++) {m_virtual_screen[i]=col;}
  }
//+------------------------------------------------------------------+
//| Retourne la couleur de la palette                                |
//+------------------------------------------------------------------+
int CIFS::GetPalColor(uchar index)
  {
   int ind=index;
   if(ind<=0) {ind=0;}
   if(ind>22) {ind=22;}
   uchar r=Palette[3*(ind)];
   uchar g=Palette[3*(ind)+1];
   uchar b=Palette[3*(ind)+2];
   return(RGB256(r,g,b));
  }
//+------------------------------------------------------------------+
//| Dessine un pixel sur l'écran virtuel                             |
//+------------------------------------------------------------------+
void CIFS::VS_PutPixel(int px,int py,uchar col)
  {
   if (px<0) return;
   if (py<0) return;
   if (px>m_xsize) return;
   if (py>m_ysize) return;
    int pos=m_xsize*py+px;
   if(pos>=ArraySize(m_virtual_screen)) return;
   m_virtual_screen[pos]=col;
  }
//+------------------------------------------------------------------+
//| Récupère la couleur du pixel depuis l'écran virtuel              |
//+------------------------------------------------------------------+
uchar CIFS::VS_GetPixel(int px,int py)
  {
   if (px<0) return(0);
   if (py<0) return(0);
   if (px>m_xsize) return(0);
   if (py>m_ysize) return(0);
    int pos=m_xsize*py+px;
   if(pos>=ArraySize(m_virtual_screen)) return(0);
   return(m_virtual_screen[pos]);
  }
//+------------------------------------------------------------------+
//| Prépare le tableau des probabilités cumulatives                  |
//+------------------------------------------------------------------+
void CIFS::PrepareProbabilities()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      m_probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
  }
//+------------------------------------------------------------------+
//| Effectue le rendu de l'ensemble IFS sur l'écran virtuel          |
//+------------------------------------------------------------------+
void CIFS::RenderIFSToVirtualScreen()
  {
   double x=0,y=0;
   double x0=0;
   double y0=0;
   uint iterations= uint (MathRound(100000+100*MathPow(m_scale,2)));

   for(uint i=0; i<iterations; i++)
     {
      double prb=1000*(rand()/32767.0);

      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=m_probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];

            int scX = int (MathRound(m_xsize/2 + (x-0)*m_scale));
            int scY = int (MathRound(m_ysize/2 + (y-5)*m_scale));

            if(scX>=0 && scX<m_xsize && scY>=0 && scY<m_ysize)
              {
               uchar c=VS_GetPixel(scX,scY);
               if(c<255) c=c+1;
               VS_PutPixel(scX,scY,c);
              }
            break;
           }
         x0 = x;
         y0 = y;
        }
     }
  }
//+------------------------------------------------------------------+
//| Copie l'écran virtuel vers le BMP                                |
//+------------------------------------------------------------------+
void CIFS::VirtualScreenToBMP()
  {
   for(int i=0; i<m_xsize; i++)
     {
      for(int j=0; j<m_ysize; j++)
        {
         uchar colind=VS_GetPixel(i,j);
         int xcol=GetPalColor(colind);
         if(colind==0) xcol=0x00;
         //if(colind==0) xcol=0xFFFFFF;
         m_bmp.DrawDot(i,j,xcol);
        }
     }
  }
//+------------------------------------------------------------------+
//| Affiche l'image BMP sur le graphique                             |
//+------------------------------------------------------------------+
void CIFS::ShowBMP(bool back)
  {
   m_bmp.Save("bmpimg",true);
   m_bmp.Show(0,0,"bmpimg","Fern");
   ObjectSetInteger(0,"Fern",OBJPROP_BACK,back);
  }
//+------------------------------------------------------------------+
//| Méthode de rendu                                                 |     
//+------------------------------------------------------------------+
void CIFS::Render(double scale,bool back)
  {
   m_scale=scale;
   VS_Fill(0);
   RenderIFSToVirtualScreen();
   VirtualScreenToBMP();
   ShowBMP(back);
  }

static int gridmode;
CIFS fern;
int currentscale=50;
//+------------------------------------------------------------------+
//| Fonction d'initialisation de l'Expert                            |
//+------------------------------------------------------------------+
void OnInit()
  {
//-- récupère le mode de la grille
   gridmode= int (ChartGetInteger(0,CHART_SHOW_GRID,0));
//-- désactive la grille
   ChartSetInteger(0,CHART_SHOW_GRID,0);
//-- crée le bmp
   fern.Create(800,800,0x00);
//-- affiche en arrière plan
   fern.Render(currentscale,true);
  }
//+------------------------------------------------------------------+
//| Fonction de désinitialisation de l'Expert                        |
//+------------------------------------------------------------------+
void OnDeinit(const int r)
  {
//-- restaure le mode grille
   ChartSetInteger(0,CHART_SHOW_GRID,gridmode); 
//-- supprime l'objet Fern
   ObjectDelete(0,"Fern");
 }
//+------------------------------------------------------------------+
//| Gestionnaire d'événements OnChart de l'Expert                    |
//+------------------------------------------------------------------+
void OnChartEvent(const int id,           // Event identifier  
                const long& lparam,   // Paramètre d'événement de type long
                const double& dparam, // Paramètre d'événement de type double
                const string& sparam  // Paramètre d'événement de type string
                )
  {
//--- clic sur l'objet graphique
   if(id==CHARTEVENT_OBJECT_CLICK)
     {
      Print("Événement de clic sur l'objet graphique avec le nom '"+sparam+"'");
      if(sparam=="Fern")
        {
         // augmente le coefficient d'échelle (zoom)
         currentscale=int (currentscale*1.1);
         fern.Render(currentscale,true);
        }
     }
  }
//+------------------------------------------------------------------+

Le résultat est:

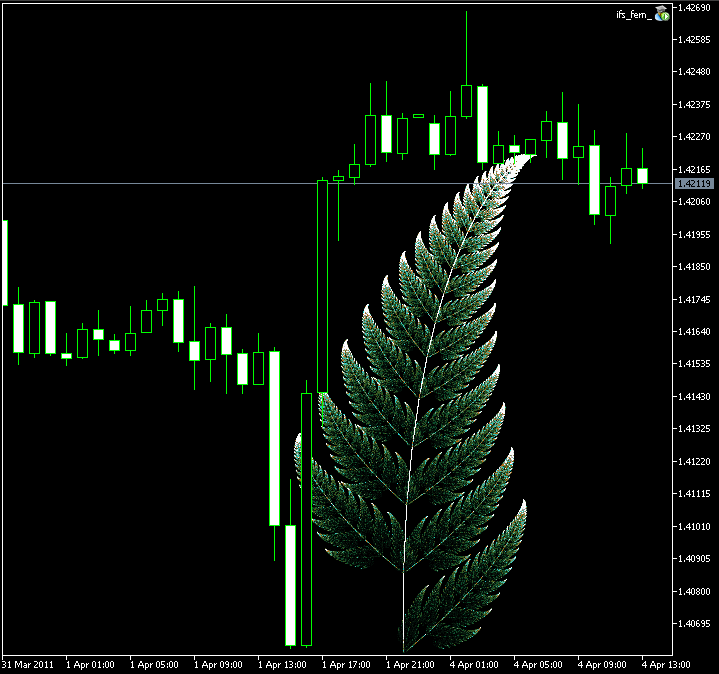
Figure 9. Image de la Fougère de Barnsley, créée avec la classe CIFS

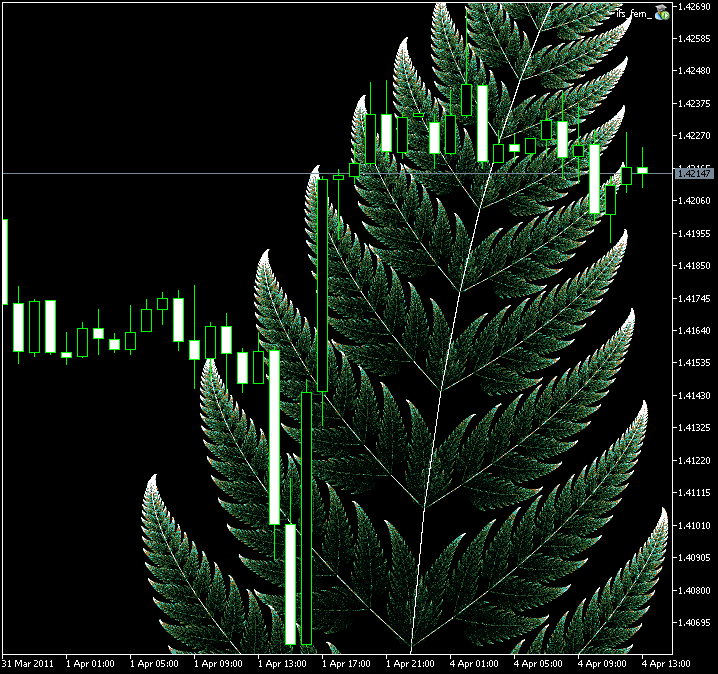
Figure 10. La région agrandie de la Fougère de Barnsley

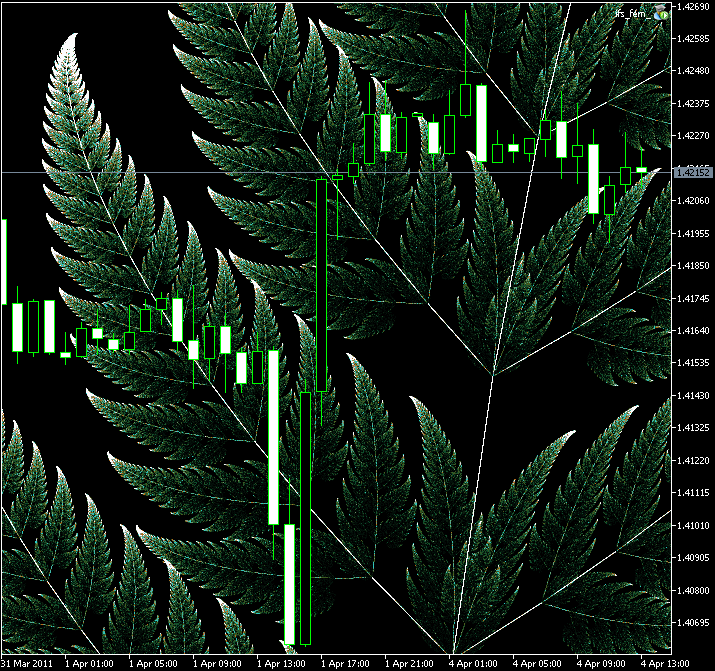
Figure 11. La région agrandie de la Fougère de Barnsley

Figure 12. La région agrandie de la Fougère de Barnsley

Fais Le Toi-Même

1. Il y a beaucoup de fractales IFS dans Fractint, par exemple :

// Binaire
double IFS_a[3] = { 0.5,  0.5,  0.0};
double IFS_b[3] = { 0.0,  0.0, -0.5};
double IFS_c[4] = { 0.0,  0.0,  0.5};
double IFS_d[4] = { 0.5,  0.5,  0.5};
double IFS_e[4] = {-2.563477,  2.436544, 4.873085};
double IFS_f[4] = {-0.000000, -0.000003, 7.563492};
double IFS_p[4] = {333, 333, 333};

// Corail
double IFS_a[3] = { 0.307692,  0.307692,  0.000000};
double IFS_b[3] = {-0.531469, -0.076923,  0.54545};
double IFS_c[3] = {-0.461538,  0.153846,  0.692308};
double IFS_d[3] = {-0.293706, -0.447552, -0.195804};
double IFS_e[3] = {5.4019537, -1.295248, -4.893637};
double IFS_f[3] = { 8.655175,  4.152990,  7.269794};
double IFS_p[3] = {400, 150, 450};

// Cristal
double IFS_a[2] = { 0.696970,  0.090909};
double IFS_b[2] = {-0.481061, -0.443182};
double IFS_c[2] = {-0.393939,  0.515152};
double IFS_d[2] = {-0.662879, -0.094697};
double IFS_e[2] = { 2.147003,  4.286558};
double IFS_f[2] = {10.310288,  2.925762};
double IFS_p[2] = {750, 250};

// Dragon
double IFS_a[2] = { 0.824074,  0.088272};
double IFS_b[2] = { 0.281482,  0.520988};
double IFS_c[2] = {-0.212346, -0.463889};
double IFS_d[2] = { 0.864198, -0.377778};
double IFS_e[2] = {-1.882290,  0.785360};
double IFS_f[2] = {-0.110607,  8.095795};
double IFS_p[2] = {780, 220};

// Etage
double IFS_a[3] = { 0,  0.52,  0};
double IFS_b[3] = {-0.5,   0,  0.5};
double IFS_c[3] = { 0.5,   0, -0.5};
double IFS_d[3] = { 0,   0.5,  0};
double IFS_e[3] = {-1.732366, -0.027891,  1.620804};
double IFS_f[3] = { 3.366182,  5.014877,  3.310401};
double IFS_p[3] = {333, 333, 333};

// Koch3
double IFS_a[5] = {0.307692, 0.192308,  0.192308,  0.307692,  0.384615};
double IFS_b[5] = {      0,-0.205882,  0.205882,         0,        0};
double IFS_c[5] = {      0, 0.653846, -0.653846,         0,         0};
double IFS_d[5] = {0.294118, 0.088235,  0.088235,  0.294118, -0.294118};
double IFS_e[5] = {4.119164,-0.688840,  0.688840, -4.136530, -0.007718};
double IFS_f[5] = {1.604278, 5.978916,  5.962514,  1.604278,  2.941176};
double IFS_p[5] = {151, 254, 254, 151, 190};

//Spirale
double IFS_a[3] = { 0.787879, -0.121212,  0.181818};
double IFS_b[3] = {-0.424242,  0.257576, -0.136364};
double IFS_c[3] = { 0.242424,  0.151515,  0.090909};
double IFS_d[3] = { 0.859848,  0.053030,  0.181818};
double IFS_e[3] = { 1.758647,  -6.721654,  6.086107};
double IFS_f[3] = { 1.408065,   1.377236,  1.568035};
double IFS_p[3] = {896, 52, 52};

//Swirl5
double IFS_a[2] = {  0.74545, -0.424242};
double IFS_b[2] = {-0.459091, -0.065152};
double IFS_c[2] = { 0.406061, -0.175758};
double IFS_d[2] = { 0.887121, -0.218182};
double IFS_e[2] = { 1.460279,  3.809567};
double IFS_f[2] = { 0.691072,  6.741476};
double IFS_p[2] = {920, 80};

//Zigzag2
double IFS_a[2] = {-0.632407, -0.036111};
double IFS_b[2] = {-0.614815, 0.444444};
double IFS_c[2] = {-0.545370, 0.210185};
double IFS_d[2] = { 0.659259, 0.037037};
double IFS_e[2] = { 3.840822, 2.071081};
double IFS_f[2] = { 1.282321, 8.330552};
double IFS_p[2] = {888, 112};

Tracez ces ensembles. Comment trouver les transformées de similarité initiales à l'aide des coefficients IFS ?

2. Créez vos propres ensembles de fractales et calculez leurs coefficients (chapitre 2).

3. Essayez de jouer avec les couleurs de la palette (tableau uchar Palette), étendez la palette et ajoutez des dégradés de couleurs.

4. Qu'en est-il de la dimension fractale (Hausdorf-Bezikovitch) de la Fougère de Barnsley ? Existe-t-il une formule de calcul de la dimension fractale à l'aide des coefficients IFS*.

5. Ajoutez le zoom d'une certaine région, en utilisant les informations sur les coordonnées du clic de souris dans OnChartEvent :

void OnChartEvent(const int id,         // Identifiant de l'évènement  
                const long& lparam,   // Paramètre de l'évènement de type long
                const double& dparam, // Paramètre de l'évènement de type double
                const string& sparam  // Paramètre de l'évènement de type string
                )
  {
//--- clic gauche
   if(id==CHARTEVENT_CLICK)
     {
      Print("Coordonnées : x=",lparam,"  y=",dparam);
     }
  }

Conclusion

Nous avons considéré l'algorithme de création d'ensembles auto-similaires utilisant le système de fonctions itérées.

L'utilisation de la bibliothèque cIntBMP simplifie grandement le travail avec les images graphiques. Outre la méthode DrawDot(x,y,color) que nous avons utilisée, la classe cIntBMP contient de nombreuses autres méthodes utiles. Mais c'est une autre histoire.