Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Gracias por el enlace, me he dejado llevar buscando ideas relacionadas. No creo que haya que enfocar la cuestión como allí, desde la perspectiva de las funciones R. Acércate con medios convencionales:
Recta de la ecuación de una circunferencia de radio R con centro de coordenadas Xc, Yc, ignorando la pérdida de significado en unidades (número, rumbo, distancia)
R^2 = (X-Xc)^2 + (Y-Yc)^2
hacemos una función de la inconsistencia en el punto con el número i (Xi = i). Es la diferencia entre la distancia del punto (Xi, Yi) al centro Xc, Yc y el radio R:
Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0,5 - R.
Los cuadrados de Di y se suman para obtener la función objetivo a minimizar. Hay tres parámetros que se pueden variar: R, Xc, Yc. Los puntos más externos (primero y último) tienen menos influencia que los intermedios (no adyacentes), creo que es mejor multiplicar por dos el Di^2 correspondiente. Y para sus propósitos de ajuste con énfasis en los últimos puntos, también puede jugar con los pesos de varios últimos puntos estableciendo una columna más para los pesos.
Si no es recto, habrá que tener en cuenta las unidades de medida. Para que X e Y influyan casi igual en el cálculo de la distancia (y R se vea afectado por ambos), es necesario tomar no i número como X, sino el mismo número multiplicado por la escala de alineación, para que los rangos X e Y sean cercanos en tamaño.
P.D. Resulta que sernam.ru se ha librado muy inteligentemente de las acusaciones de violación de los derechos de autor publicando los textos de los libros sólo por partes y sin especificar los datos de salida, en particular los títulos de los libros. En sernam.ru es posible encontrar textos que no se encuentran en ningún otro lugar de Internet.
He descubierto que tengo que minimizar utilizando Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0,5 - R.
Entonces será necesario trazar el círculo encontrado por juegos.
la ecuación será.
y=(R^2-(X-Xc)^2)^0.5+Yc
Por lo tanto, no pierda su tiempo con esta dirección. Aunque, puede construir un indicador basado en un arco, en lugar de una línea recta, como el mashka. tal vez funcione mejor que el sma.
esta es la fórmula que tomé.
la ecuación general del arco:
(x - L)^2+ (y + (R - H))^2 = R^2
y = sqrt(R^2 - (x - L)^2) - (R - H) , donde la fórmula de R está en la figura.
Pero sólo sirve para el plano positivo. Para el experimento tomé un "canal de precios en arco" que se encuentra en el plano positivo.
tal vez sólo sea un nombre bonito elegido...
RRR5:
...
Pero esto sólo sirve para el plano positivo. Para el experimento tomé un "canal de precios en un arco", que se encuentra en el plano positivo.
¿Qué es un "plano positivo"?
¿Qué es el "plano positivo"?
pero no este arco.
Bueno, para un arco como este, funcionará.
pero no para este.
RRR5, haces dibujos rápidamente. ¿Con qué, me pregunto?
Leo aquí sobre polinomios, CNA, diversos métodos de aproximación, capacidad de previsión, etc...
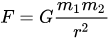
Algunos creen en la predicción, otros no.
Pero lo que esperaba encontrar, nunca lo vi.
Para intentar explicar lo que quiero decir, recurriré a una analogía con la gravedad en el universo.
Aquí puedes ver el gif animado que grabé.
Responda usted mismo a la pregunta. ¿Es posible predecir la trayectoria de cada objeto?
Pues claro que sí.
Pero sólo si se conoce la información de cada objeto en el momento: su masa, posición actual y dirección del movimiento, hora de su aparición y hora de su desaparición.
Y luego es cuestión de matemáticas y cálculos, utilizando esencialmente una sola fórmula (para una variante de la mecánica clásica para velocidades alejadas de la velocidad de la luz):
el propio programa es un atasco de gravedad aquí. Puedes jugar con él.
También es necesario entender que incluso nuestro planeta no se mueve en un círculo cerrado, sino que en realidad es una onda sinusoidal tridimensional (espiral).
Este vídeo lo demuestra claramente:
¿Y qué pasa si no tenemos información sobre todos los objetos?
¿Podemos predecir la trayectoria conociendo sólo la propia trayectoria en el pasado?
Aquí es donde comienza la diversión.
Si alguien dice que no es posible, la respuesta es errónea. Una respuesta afirmativa también sería errónea.
La solución a este problema sólo será probabilística.
El problema debe resolverse desde la dirección opuesta. En función de la trayectoria pasada, debemos calcular primero las trayectorias probabilísticas de los principales "grupos" de objetos y su masa. Para luego predecir modelos probabilísticos de posibles trayectorias.
Para eso está la tarea básica de la IA: el reconocimiento de patrones.
Según tengo entendido, a esto se refería Maxim Dimitrievski.
Hace unos seis años, publiqué mis primeros avances en este ámbito en la KB:https://www.mql5.com/ru/code/10882. Sólo utilicé un polinomio de grado 1 (Regresión Lineal) para el reconocimiento de canales allí. Después he avanzado mucho en este ámbito. Pero no publico nada y no lo haré por razones obvias. Sólo doy pistas para las mentes inquietas.
Encontrar canales lineales es esencialmente encontrar los centros de estas masas gravitacionales.
Normalmente hay entre 5 y 10 de estos centros (canales) en cualquier instrumento (símbolo). Para la predicción del precio deben tenerse en cuenta todos ellos simultáneamente. Sólo en este caso la precisión de la predicción al alza o a la baja será muy superior al 50%.
Pero todo el mundo trata de encontrar un conjunto especial de números y cree ingenuamente que predice el futuro.
La cuestión es que este "conjunto de números" vivo, dinámico, cambia constantemente, así como la posición de los centros locales de masas del conjunto de objetos en analogía con una gravitación material cambia. Y el problema se reduce a encontrar la ley de cambio de este "conjunto de números" e incluso encontrar la ley de cambio de la propia ley :))
Lo ideal es que este "conjunto de números" se recalcule con cada tic. Precisamente por eso he dicho más de una vez que lo que muchos llaman optimización, la búsqueda de un "conjunto de números" concreto, es una trivialidad de los datos históricos.
Creo que la analogía con la gravedad es muy acertada. En el mercado, la gravedad la crea el dinero. Algunos irán con 100 dólares, otros con unos cuantos miles de millones. Aquí se aplican las mismas leyes de la gravedad, e incluso la misma fórmula que he dado antes. La fuerza de atracción es inversamente proporcional al cuadrado de la distancia y directamente proporcional a las masas. Por lo tanto, una regresión polinómica de grado 2 (parábola) es la herramienta más adecuada. Aunque sería más lógico utilizar una hipérbola, porque es según las leyes de la hipérbola que dos cuerpos gravitatorios interactúan. Pero, el hecho es que la parábola es mucho más conveniente para los cálculos, así como la parábola y la hipérbola son muy similares entre sí en el intervalo más importante.
Aquí lo puedes ver claramente. La línea roja es la parábola y la azul es la hipérbola.
La principal diferencia entre la gravedad del dinero y la de los cuerpos celestes es que el dinero puede aparecer y desaparecer repentinamente, creando poderosas fluctuaciones gravitacionales. Pero para calcular este evento, y existe una cosa como una ruptura del canal.
La solución a este problema sólo será probabilística.
El problema debe resolverse a la inversa. A partir de la trayectoria pasada, hay que calcular primero las trayectorias probabilísticas de los principales "grupos" de objetos y su masa. Para luego predecir modelos probabilísticos de posibles trayectorias.
Me temo que la "solución probabilística" en este caso sería el conjunto de cualquier trayectoria en un espacio determinado, ¿y cuál es el valor de esa solución?
Eso sería como afirmar "con alta probabilidad" que el eurodólar no será negativo este año, no más de 100. Obsérvese que la probabilidad de esta afirmación se acerca al 100%. Pero, ¿te serviría de mucho esa "predicción"?
En la teoría de la probabilidad, se demuestra que cuando el estado de un objeto está influenciado por muchas fuerzas independientes, la probabilidad del estado empieza a obedecer la ley de Gauss. Sin embargo, el curso y el valor de los precios no obedecen a esta distribución, por la sencilla razón de que las entradas y salidas de los participantes en el mercado son dependientes.
RRR5:
понял, что минимизировать нужно по формуле Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R.
...
Para el experimento tomé un "canal de precios en un arco", que se encuentra en el plano positivo.
Sigo sin entender por qué no te gusta el MNC. Construye cualquiera de esas curvas normalmente, ¿no?
Me gusta trabajar en TFs pequeños, pero no me gustan estos caramelos.
¿Con qué puede predecirlos?