Impulso - página 7

[Renat Akhtyamov]

Олег avtomat:
No entiendo... ¿qué hay en la parábola?

¿cómo se vería todo si se insertara una parábola en lugar de una función?

[[Eliminado]]

añadir un poco de crecimiento cuadrático rápido (obtener una parábola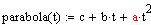 con oscilaciones superpuestas)

[[Eliminado]]

new-rena:
¿Qué aspecto tendría todo esto si se sustituyera la función por una parábola?

Pues bien, una parábola también es una función.

[Vladimir Karputov]

Олег avtomat:

añadir un poco de crecimiento cuadrático rápido

Correlaciones interesantes. ¿Y el cambio en el precio de las divisas puede describirse aproximadamente con qué ecuación de las que has dado?

[[Eliminado]]

Karputov Vladimir:
Correlaciones interesantes. Pero el cambio en el precio de las divisas puede describirse a grandes rasgos con qué ecuación de las que has citado?

Lo aclaré allí, queriendo decir una parábola

[Renat Akhtyamov]

Олег avtomat:

Lo aclaré allí, queriendo decir que la parábola

Ya veo. Más simple: s(t)=parábola, ¿qué obtienes?

[[Eliminado]]

new-rena:
Ya veo. Más simple: s(t)=parábola, ¿qué obtienes?

Una parábola es una recta de segundo orden. Su aceleración es una constante, por lo que la derivada de la aceleración (jerk) es cero :

[Renat Akhtyamov]

Олег avtomat:

Una parábola es una recta de segundo orden. Su aceleración es una constante, por lo que la derivada de la aceleración (jerk) es cero :

Ah, bueno, sí. Es decir, ¿es posible que en jerk=0 haya un principio/final de impulso?

[[Eliminado]]

Karputov Vladimir:
Correlaciones interesantes. Pero el cambio en el precio de las divisas se puede aproximar mediante cuál de las ecuaciones que has citado?

Si no imponemos ningún requisito de proximidad (como el MOC, etc.), esta formulación es incorrecta.

El mismo intervalo de movimiento de precios puede describirse mediante una línea recta, o mediante una sinusoide, o mediante un conjunto complejo de componentes diferentes. Todo dependerá de los propósitos de dicha descripción, y estos propósitos dictan un grado aceptable de aproximación a la serie original.

[[Eliminado]]

new-rena:
Ah, cierto. Es decir, ¿es posible que en jerk=0 haya un impulso de inicio/fin?

El movimiento real nunca será una parábola pura, incluso suponiendo que no haya oscilaciones superpuestas, ya que siempre hay ruido presente que hace que charle no sólo la tercera derivada (es decir, el tirón != 0 ), sino también las derivadas de órdenes superiores.