You are missing trading opportunities:
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register
It is obvious that you should withdraw q and only at the end of period t. In all other cases the amount withdrawn will be less than
The hedgehog has decided to use analytical calculations))))
The problem has no extremes, because we have a monotonically increasing numerical series - a function with an argument in the form of the size of the deposit. I.e. there is nothing to optimize. The greater the argument and t, the greater the value of the function. In any other case the value of the function will decrease.
It's hard to look for a black cat in a dark room, especially if it's not there (c) Confucius
All that's left is to take the time derivative and equate it to zero... Yeah.
By the way, if anything, the derivative should be taken over k
Pardon! Really on the k .
Reshetov:
It's obvious that you have to withdraw q and only at the end of period t. In all other cases the amount withdrawn will be smaller.
Yura, you're so confident that it's funny when you're wrong.
On the first page, avtomat gave a picture where you can clearly see the optimum on the parameter k . Maybe you just did not notice. I will show you another one:
Do you see the maximum? No? But it is there!
Take a rest, you hedgehog.
No way!...
Can you be more specific? I mean, in the form of a formula.
In other words, the optimum in terms of the withdrawal percentage is indeed visible!
I recently solved a similar problem...
And then we combine all this together and get the resulting function of two variables.
It should also be mentioned that the result depends on the optimization period, i.e.
the optimum for 12 months is not equal to four optimums for 3-month periods.
I recently solved a similar problem...
That's right, avtomat. That's exactly how it behaves. But I really need to get an analytical solution for the optimal fraction of k. If you take the derivative of k from f(k), you get the following equation: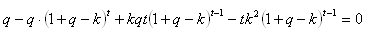
The figure below clearly shows that the abscissa where df/dk is zero coincides with the maximum of f(k).
But how to solve it with respect to k?
Well the problem has nothing to do with trading anyway. It is a problem about the rentier. It would be quite appropriate for that branch.
P.S. I wonder, what will do Jura in this situation? Is he going to pretend that he hasn't noticed anything (no maximum on the parameter k ) and leave no comments on the subject or he'll have to reconsider his basic assumptions for life...
P.S. I wonder what Jura will do in this situation? Will he pretend not to notice anything (no maximum for parameter k ) and leave no more comments on the subject or will he have to reconsider his main set points for life...
I have been allowed to use a deposit of X0 rubles for t months. Every month the deposit gets a fixed percentage q of the current value of the deposit X. I am allowed to withdraw a certain percentage k from the account every month which does not exceed the value of q.
I am allowed to open trades with HO lot size. Each open positive trade has a u% chance to accumulate w pips, while earning q of course from the current value of the XO deposit. I am allowed to partially close an order by a certain percentage k as many times as I wish (up to 100% close) with a frequency of n pips which does not exceed w.
Question: Find relative to u%, optimal values of k, n.
That's right, avtomat. That's exactly how it behaves. But I really need to get an analytical solution for the optimum fraction of removal k. If you take the derivative of k from f(k), you get the following equation:
The figure below clearly shows that the abscissa where df/dk is zero coincides with the maximum of f(k).
But how to solve it with respect to k?
if the above equation is true, then we can do so:
But again, what are the requirements, what are the conditions...
q and t -- given constant quantities or ...