[Archive!] Pure mathematics, physics, chemistry, etc.: brain-training problems not related to trade in any way - page 309

New comment
 

YUBA, the phrase "randomly" does not quite fit here.

 

In short, the answer (337) is one.

 
Justification, Richie?
I.e. can you name such an arrangement of numbers, in which the one on the hundredth place will not move anywhere neither in the first, nor in the second time?
P.S. The problem somewhat resembles the first one in this thread (about Peter): it seems as if the conditions are not enough, and almost any number fits.
 

I get it now. I'll think about it :) Tomorrow, I can't think now.

 
Mathemat >>:
Ну ты даешь. Я надеялся на интригу...
Доказывай.

I don't know how to prove... And I don't like... It's not my thing... It's my thing to find answers. // And find them... :)

// Damn. I used to love it. I used to love it.

.....

I'll give it a shot. Firstly I'll point out the fact that finding "100" at position 100 is still an insufficient condition for immobility, but only necessary.

Besides that, all numbers smaller than 100 must initially be in places smaller than 100 (in any order). The others, respectively, on the remaining ones - also in any order.

I'll try to prove it the other way around. // that's how nasty I am.

If at least one number in places 1...99 >= 100, then on the first pass it will be caught by the sorting process and will move from left to right, until it meets an even larger number. If this happens, it will remain "in the meeting place" and a new maximal number will crawl to the right instead. Crossing the "boundary" (100) the maximal number will inevitably "move" the number standing there if it turns out to be smaller than it. At this point, you can stop analyzing the first pass and move on to the second. If at least one number in the 'number places' range 101...1982 is less than or equal to 100, it will be caught by the process and begin to move left.... etc. (see the description of the first pass in the mirror). So there is only one way to leave the number on 100 stationary: put the number 100 there and make sure all numbers less than 100 are clearly pre-grouped to the left of 100, and all larger numbers are pre-grouped to the right, respectively.

That's all I can say about it. I have no idea how much of a proof it is, but I've kind of provided the obviousness. // At least for myself )))

 
You convinced me, Volodya. I had the same reasoning. About the necessity of the condition - yes, very accurately noted. And the answer is the same. OK, next:
 

In my mother-in-law's opinion: it's the number 1981, not 100 :)

 
Mathemat >>:

Все равно не хватает. Где контакты, между которыми измеряется ток? Сетка может быть полубесконечной с началом в начале координат и первым контактом. Тогда достаточно перекусить два.

А если один из контактов - где-нить в центре сети, то достаточно четырех - вокруг него.

I agree. I'll redo it now. :)

That's the way it's worded.

 

Dim a, b, c, d, i, i, z As Long
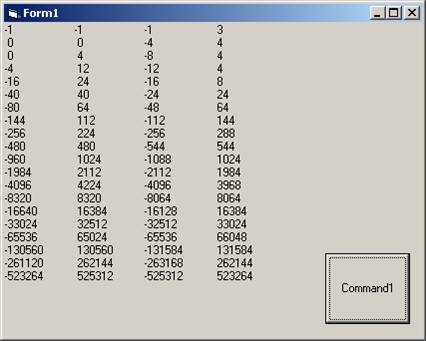
Private Sub Command1_Click()
a = 1
b = 2
c = 3
d = 4
For i = 1 To 20
z = a
a = a - b
b = b - c
c = c - d
d = d - z
Print a, b, c, d
Next i
End Sub

 
Richie >>:

Dim a, b, с, d, i, z As Long
Private Sub Command1_Click()
.......... ...
Next i
End Sub

..........

Now prove the inevitability.
// By the way, the fact that degrees of twos are represented in the sequence in huge numbers is surprising. Also inevitability?
1...302303304305306307308309310311312313314315316...628
New comment