[Archive!] Pure mathematics, physics, chemistry, etc.: brain-training problems not related to trade in any way - page 304

New comment
 
Let F(x,y) = min( x, y + 1/x, 1/y ), then
F(1/y, 1/x) = min( 1/y, 1/x + y, x ) = F(x,y).
Hence, the minimum if you replace y with 1/x and x with 1/y will not change. Y = 1/x.
So F(x,1/x) = min( x, 2/x, x ) = min( x, 2/x ). It equals x if x < sqrt(2), and 2/x otherwise.
Draw both curves y=x and y=2/x. Obviously, the maximum is exactly at the point of their intersection and equals sqrt(2).
The solution in the problem book is rather vague, I don't like it:


Next (8th):

This part is trivially constructed. Let's leave the intrigue behind.
The second part of the problem (also 8th):
 
Another follow-up is geometric (8th):
 

Simplified the figure:

 
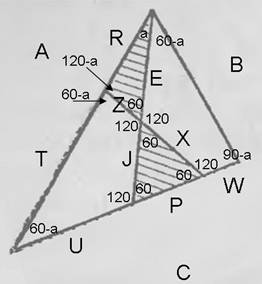
Richie, how come there are equal angles in a shaded triangle?
 
Mathemat писал(а) >>
Richie, how come there are equal angles in a shaded triangle?
In the central one? It's obvious.
 
Go on, then. Prove it.
By the way, the problem statement doesn't say anything about the original triangle being equilateral. Although it is drawn like an equilateral one.
 
Mathemat писал(а) >>
Come on. Prove it.

I haven't figured out how yet. I'll think about it.
-
Well, anyway, the idea was this:
The area of a 4x triangle is equal to one third of the difference of the area of the large triangle and the 4 small triangles, i.e. 4 sq.cm.
To find the area of the large triangle you need to find its side (in the figure - A).
Find the side of the central triangle by area, knowing that it is equilateral is not a problem, it is equal to sqr(4*S/sqr(3)).
 
Richie >>:
В центральном? Это очевидно.


Only if the three triangles (apart from the central one) are the same
But that's not a fact according to the conditions
 
That's not a fact.
There has to be something to hold on to. There is one lead, but I don't know what to do with it yet.
 
Mischek писал(а) >>

Only if the three triangles (apart from the central one) are identical.
But that's not a fact.

Well you've got me completely confused.
I thought the big triangle was equilateral. The small 3 triangles are equilateral, so as a consequence they are similar.

1...297298299300301302303304305306307308309310311...628
New comment