Hearst index - page 45

New comment
 

Version R 3.0.0 is now available.

Everything has to be reinstalled, including RStudio.

By the way, does anyone know how to get rid of the mandatory 4 windows.

 

faa1947:  

By the way, does anyone know how to get rid of the mandatory 4 windows.

By dragging the vertical and horizontal borders you can hide the windows you don't need.
 
WWer:
By dragging the vertical and horizontal borders you can hide windows that are not needed.
Indeed, thank you.
 

By the way, if anyone is interested:

Pull up Renko on the chart to exactly the first knee of the Zigzag from and to the pick.

And on the zero knee, see the lag or advance of the beginning of Renko relative to the peak of the Zigzag.

The system is set up like a fib, but the result is a curve in the basement from the zero level.

 

Not so long ago fate brought me into contact with this topic and several questions immediately arose. Dear experts, can you help me to find answers to these questions? Don't kick me if any of the questions seem silly to you...

So:

1) There are several ways of finding the Hurst index. Which of these ways (in your opinion) is the best (gives a more accurate estimate of the index)? If possible, provide a link to the source.

2) Should the indicator be invariant under linear transformations? (A detailed answer is desirable).

3) If the series are correlated with each other, what can be said about the Hurst index?

4) There are three series. A Hurst index is calculated for each series. When the series are added together, what can be said about the exponent?

I thank you in advance.

 

Should we start a separate thread on the use of the R language? Share experiences and results.

Of course, if anyone is interested.

Good luck

 

I went back to the analysis of this non-trivial indicator again. For a long time I was confused by the side coefficient obtained by calculating the Hearst value. Essentially, Hearst is a linear equation in double logarithmic scale, where on the ordinate axis (Y) is given the distance travelled by the price in the adjusted scales, and on the abscissa axis (X) - a specific period (timeframe or horizon). This linear equation is an approximation of the points that we have experimentally measured and plotted. The formula for the equation is simple and obvious:

Let's pretend for a while that the coefficient is zero and simplify the formula to 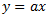. The value 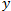here is the distance traveled by the price. The value 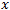is the time period. Obviously, in a classical Brownian motion the price travels a distance corresponding to the square root of , where 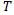is the time or period:

This equation is a special case of our formula, at :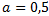

This formula in double logarithmic scale will correspond to our linear function proper:

Where 0.5 is the Hurst coefficient.

All these calculations are trivial, but they neglect the awkward coefficient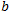 , which in reality is almost always a significant number. So how do we understand this coefficient? My mathematical reflections on the nature of this dependence have led to an understanding of this coefficient. After all, it only appears when we approximate our empirical points by a linear function. For each particular point, its H is always known. It does not have the coefficient because there is no general approximating function for it either. Let's consider a simple example, let's try to calculate H visually for points C and D R/S of the EURUSD chart:

For point C it is approximately 0.45, for point D it is 0.51. Since both points lie almost perfectly on the approximating line(y = 0.5304x - 0.0757 ) we can calculate the exact values of H for these points analytically. For C:

For D:


By performing the inverse transformation for D, for this point the Y value is 1.5155 and the X value corresponds to 3, then its H will be:

The result of the calculation shows that point C is antipersistent (H = 0.4547) and D is actually Brownian (H = 0.5051). The estimation of H for the entire series becomes meaningless, because on a small horizon the series is anti-trendy, while on a larger horizon it tends to become more trendy. This is fully consistent with empirical observations about currencies. Everyone who trades them long enough sees that on small scales prices constantly fluctuate in the flat, and on larger scales, lasting a year or more, there are large trend movements.

The coefficient is a kind of relativistic correction in physics. It forms a correlation with H and determines the change of the market character with the increase of scale. If this coefficient is close to zero, the market is homogeneous in its scale. The trendiness or antipersistence in it is approximately at the same level regardless of the scale. If b is significant - it is the dominant initial condition. H - it starts to dominate more with increasing scale. Here are the types of relationship between H and:

  • H is greater than 0.5; b is a negative number. With this combination the market is anti-trend at small scales, but as the time frame increases trends start to appear. This behaviour is exhibited by currencies;
  • H is greater than 0.5; b is a positive number. The market is homogeneous. Trends dominate at all time scales. If H is significant and b is not significant, the stronger trends are more often seen on greater time horizons. The longer the horizon, the stronger the trends are. On the contrary, if H is not considerable and b is big - stronger trends can be found on small time scales, and as the period grows, the trends keep appearing but their strength and purity decreases.
  • H is less than 0.5; b is a negative number. The market is antipersistent at all scales. If H is significant and b is not - more frequent and cleaner returns to the mean occur on larger timeframes. On smaller timeframes price is more prone to random wandering. If, on the contrary, b is significant and H is not - the market is more prone to come back on small timeframes, on longer timeframes the market is closer to a Brownian motion, but still maintains its antipersistence.
  • H is less than 0.5; b is a positive number. With this combination, the market is trending at small scales, but becomes anti-trend at larger mastshafts. Apparently such behaviour was observed in the period of oil price in the region of $100 per barrel.

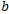If b modulo is a significant fraction of H, then you cannot limit your analysis to H. The market can exhibit two opposite properties at different time scales, e.g. being trending and counter-trending at the same time.

If H and b are significant and point in different directions (H is significantly more than 0.5 and is negative or H is significantly less than 0.5 and b is positive) - the market shows sharp changes from one state to another depending on the timeframe.

 

Has anyone implemented the time indicator formula shown here:

http://cdn.scipeople.com/materials/2667/%D0%9F%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5%20RS%20%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0%20%D0%BD%D0%B0%20%D1%84%D0%BE%D0%BD%D0%B4%D0%BE%D0%B2%D1%8B%D1%85%20%D1%80%D1%8B%D0%BD%D0%BA%D0%B0%D1%85%202.doc

5 countries

 
Is there a Hearst indicator for MT4?
 
By the way, there is an indicator called the invariance index. It looks at the slope of the regression line, thus answering the question whether there is a trend in the market or not. I still have not got time to use it, but I want this index to calculate not the price movement in the market, but the movement of balance curve. It would allow to see if there is balance change or not. We determine the direction, if it is going upwards, we mirror the signals, if it is going upwards, we repeat it. It seems to me that any system may be pulled out by the ears with such a helper .... I think any TS can be pulled out by the ears with such a helper... What do you think?
Files:
ivar.mq4  4 kb
1...383940414243444546
New comment