Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Leute, die mit solchen Worten um sich werfen, ich gehöre nicht hierher.
Ich lese und versuche herauszufinden, worauf sie sich einigen werden.
Wenn es der erste Versuch eines anderen Lamms ist, einem Oktopus ein Paar Rüschen anzuziehen, ist das eine Sache. Wenn es etwas Praktisches ist, werde ich mitmachen.
Also kam Neutron und brachte alles an seinen Platz. Übrigens, marketeer spricht auch von Kurtosis und Asymmetrie.
Die entsprechende Gauß-Kurve kann nach Belieben gezeichnet werden, aber hier ist es am einfachsten, einfach die Stichprobenvarianz zu berechnen und eine Gauß-Kurve mit den Parametern 0 und sigma zu zeichnen. Dann können Sie den Unterschied zwischen einem echten Histogramm und einer solchen Gauß-Kurve erkennen.
Übrigens sollte diese Gaußsche Näherung in der Mitte der Kurve (am Nullpunkt) deutlich niedriger sein als das echte Histogramm.
Urain, mit wie viel haben Sie den c.p.s. der Proben multipliziert?
Andererseits hängt der c.s.o.-Schätzwert für eine stark schwanzlastige Verteilung vom Stichprobenumfang ab, so dass es hier nicht so einfach ist.
Ich habe den Effektivwert überhaupt nicht verändert, sondern nur ein vorgefertigtes Diagramm genommen und es so skaliert, dass es vertikal in das Histogramm passt.
Das Histogramm ist die Verteilung der Clos-Differenz (es hat MO und RMS), und diese MO und RMS werden verwendet, um die rote Linie mit Hilfe der obigen Formel zu konstruieren, aber da die Linie am unteren Ende des Histogramms verloren geht, und wegen des kleinen absoluten x für die Konstruktion eines proportionalen y-Histogramms, mussten wir jede y-Linie mit einem Multiplikator zum Vergleich multiplizieren.
Für die Benchmark-Funktion werden die Varianz und MO aus einer Reihe von Zitaten (auch dort berechnet) entnommen und auf den gleichen Wert gesetzt, aber die einzige Manipulation ist mit den absoluten Werten der Benchmark, hier müssen wir jeden Term zum Koeffizienten addieren, um die Scheitelpunkte zu kombinieren.
Soweit ich weiß, ist die Referenzfunktion eine HP-Funktion.
Wenn ja, haben Sie alles richtig gemacht, außer einer Sache: Sie können keine Domains verwalten. Ihr Wunsch, Eckpunkte zu kombinieren, hat nichts mit der tatsächlichen Lage der Graphen zu tun. Außerdem verstößt das Domaining gegen die Normalisierung der HP-Funktion. Wie gefällt Ihnen die Wahrscheinlichkeit >1 ?
Wenn Sie die Beherrschung entfernen und das Bild noch einmal machen, werden die Flächen in der Breite mehr oder weniger gut übereinstimmen. Das Histogramm wird jedoch in der Mitte und an den Rändern höher sein, was auf zwei Hauptprobleme hinweist: eine höhere Ausbeute und gleichzeitig starke Ausläufer.
Machen Sie ein Bild wie dieses, wenn es Ihnen nichts ausmacht.
PS
Ich verstehe Ihr Problem aus dem vorherigen Beitrag. Es besteht keine Notwendigkeit, gegen die HP-Normierung zu verstoßen. Es ist besser, die richtige Skala für das Histogramm zu finden. Es wird von der gleichen Rationierung gefunden. Sie müssen die Höhen aller Balken im Histogramm addieren und dann jeden Balken durch diesen Wert dividieren. Das Ergebnis ist, dass auch das Histogramm auf 1 normalisiert wird.
Ich lese - und versuche herauszufinden, worauf sie sich einigen werden.
Wenn es ein weiterer erster Versuch ist, einem Tintenfisch ein Paar Rüschen anzuziehen, ist das eine Sache. Wenn es etwas Praktisches ist, bin ich dabei.
Versuchen Sie herauszufinden, was in der ersten Differenz einer Reihe von Zitaten enthalten ist, die nicht in der Normalverteilung enthalten ist?
Ich versuche herauszufinden, was in der ersten Differenz der Zitatserie enthalten ist, das in der Normalverteilung nicht vorhanden ist.
Und was ist der Zweck, was ist das Ziel? Um Bereiche mit "Anomalien" zu identifizieren? Nochmals: Warum?
(Bislang nur "?????")))
Und was ist der Zweck, was ist das Ziel? Bereiche mit "Anomalien" identifizieren? Nochmals: Warum?
(Bislang eine "?????")))
Sagen wir, um zu untersuchen, welches Gesetz der Abnormität sich manifestiert.
Meines Erachtens ist die Referenzfunktion eine HP-Funktion.
Wenn ja, haben Sie alles richtig gemacht, außer einer Sache: Sie können keine Domains verwalten. Ihr Wunsch, Eckpunkte zu kombinieren, hat nichts mit der tatsächlichen Lage der Graphen zu tun. Außerdem verstößt das Domaining gegen die Normalisierung der HP-Funktion. Wie gefällt Ihnen die Wahrscheinlichkeit >1 ?
Wenn Sie die Beherrschung entfernen und das Bild noch einmal machen, werden die Flächen in der Breite mehr oder weniger gut übereinstimmen. Das Histogramm wird jedoch in der Mitte und an den Rändern höher sein, was auf zwei Hauptprobleme hinweist: eine höhere Ausbeute und gleichzeitig starke Ausläufer.
Machen Sie ein Bild wie dieses, wenn es Ihnen nichts ausmacht.
PS
Ich verstehe Ihr Problem aus dem vorherigen Beitrag. Es besteht keine Notwendigkeit, gegen die HP-Normierung zu verstoßen. Es ist besser, die richtige Skala für das Histogramm zu finden. Es wird von der gleichen Rationierung gefunden. Sie müssen die Höhen aller Balken im Histogramm addieren und dann jeden Balken durch diesen Wert dividieren. Das Ergebnis ist, dass Ihr Histogramm ebenfalls um 1 normalisiert wird.
Nun, so schlimm ist das nicht. Sie müssen es noch normalisieren.
Nun, es gibt überhaupt keine Rationierung. Nur beide sind auf Multiplikator=1,0/Punkt eingestellt, sonst sieht der Induktor nicht so kleine Werte.
. Links unten ist die Wahrscheinlichkeitsverteilungsdichte, rechts die gleiche in logarithmischer Skala.
Wäre die Verteilung normal, hätten wir es hier mit einer Parabel zu tun, was aber wegen der "fetten" Schwänze nicht der Fall ist. Im Prinzip sollten wir hier einen Gaußschen Kleinstquadratwert einsetzen, dann passt alles zusammen. Ich muss eine Formel für die optimale Passform aufstellen...
Sergej, was ist mit dem doppelten Logarithmus? Ich habe schon eine Weile darüber nachgedacht...
Aus Bescheidenheit kann ich es nie testen :)
Sergej, was ist mit dem doppelten Logarithmus? Ich habe schon seit einiger Zeit darüber nachgedacht...
Ich bin zu bescheiden, um es zu überprüfen :)
Es stellt sich heraus, dass dem so ist:
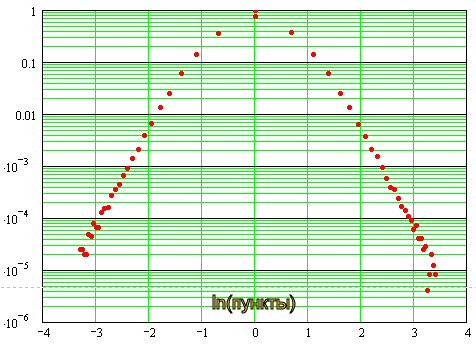
Es ist zu erkennen, dass die Verteilung in der Nähe von Null nahe an der Normalverteilung liegt und dann asymptotisch in Form von Geraden verläuft, was auf einer doppelt logarithmischen Skala den exponentiellen Charakter der Verteilung der "Schwänze" anzeigt. Mit anderen Worten: über ihre "Schwere".