Maschinelles Lernen im Handel: Theorie, Modelle, Praxis und Algo-Trading - Seite 436
Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Es klappt, danke! Interessant, wie das funktioniert...
Wird eine Option mit der größten Ähnlichkeit gesucht oder wird ein Durchschnitt über mehrere Optionen gebildet? Offenbar findet es 1 besten. Ich denke, ich sollte mich für 10 oder sogar 100 Varianten entscheiden und nach der durchschnittlichen Vorhersage suchen (die genaue Anzahl sollte vom Optimierer bestimmt werden).
Ja, hier zeigt es 1 am besten, habe mich nicht mit vielen Varianten beschäftigt, du kannst versuchen, es nachzumachen, wenn du meine Schrift verstehst)
Ich habe nie lernen können, wie man nur mit den Preisen gewinnbringend handelt. Aber das Mustermodell schon, also ist die Wahl offensichtlich :)
Es ist eine Sache, ein "Muster" zu finden, aber es ist eine ganz andere Sache, wenn es einen statistischen Vorteil bringt. IMHO bezweifle ich das aus irgendeinem Grund sehr stark. Die Suche nach Mustern durch Faltung (Produkt, Differenz) über die gesamte Länge einer historischen Reihe mit Mittelwertbildung ist in der Tat wie eine Regression in NS mit EINEM NEURON, dem einfachsten linearen Modell mit extrem dummen Vorzeichen, einem Stück Preis, wie es ist.
Es ist eine Sache, ein "Muster" zu finden, aber es ist eine andere Sache, einen statistischen Vorteil zu finden. IMHO bezweifle ich das sehr. Die Suche nach Mustern durch Faltung (Produkt, Differenz) über die gesamte Länge historischer Reihen mit Mittelwertbildung ist in der Tat wie eine Regression in NS mit EINEM NEURON, dem einfachsten linearen Modell, mit extrem dummen Merkmalen, einer Scheibe des Preises, wie es ist.
Wenn es sich um ein einzelnes Neuron handelt, dann mit einer Anzahl von Eingängen, die der Länge des Musters entspricht (Muster von 30 Takten = 30 NSb-Eingänge von 500 Takten = 500 NS-Eingänge).
Meiner Meinung nach sind viele Neuronen in den inneren Schichten des NS analog zum Gedächtnis, 10 - 50 - 100 zusätzliche Neuronen sind entsprechend 10 - 50 - 100 gespeicherte Varianten von Eingangssignalen. Und wenn wir das Muster mit 375000 Varianten aus der Geschichte (M1 für ein Jahr) vergleichen, haben wir ein absolut genaues und vollständiges Gedächtnis anstelle von 10 -50 - 100 am häufigsten auftretenden Varianten. Aus diesem Speicher ermittelt der Musterfinder dann die N ähnlichsten Ergebnisse und erhält die durchschnittliche Vorhersage, während das neuronale Netz die Gewichte der Verbindungen zwischen den Neuronen bei jedem ähnlichen Muster erhöht.
Es ist nicht klar, warum die Faltung angewandt werden soll, ich nehme an, dass Sie vorschlagen, das gesuchte Muster mit jeder Variante aus der Geschichte zu falten, als Ergebnis erhalten wir die 3. zeitliche Sequenz - und wie hilft es, die Ähnlichkeit des Musters und der geprüften Variante zu bestimmen?Wenn es sich um ein Neuron handelt, dann entspricht die Anzahl der Eingänge der Länge der Vorlage (Vorlage mit 30 Balken = 30 NS-Eingänge mit 500 Balken = 500 NS-Eingänge).
Eine weitere Sache, die nicht klar ist, ist, warum die Faltung angewendet werden sollte, ich nehme an, dass Sie vorschlagen, das gesuchte Muster mit jeder Variante aus der Geschichte zu falten, als Ergebnis erhalten wir die dritte zeitliche Sequenz - und wie hilft es, die Ähnlichkeit von Muster und getesteter Variante zu definieren?
Ja, hier ist 1 am besten zu sehen, ich habe mir nicht die Mühe gemacht, viele Varianten zu machen, du kannst versuchen, es nachzumachen, wenn du meine Schrift verstehst)
wenn ich mir das Bild ansehe, stimmt etwas nicht...
Hier ein zufälliges Beispiel
Ihre blaue Prognoselinie geht sehr steil nach unten, mit einer schwachen Bewegung einer ähnlichen Variante...
Hier ist gerade diese Variante gephotoshopt und es sieht nicht so steil aus und macht von der Idee her mehr Sinn.
während ich mir das Bild ansehe, stimmt etwas nicht...
Hier ein zufälliges Beispiel
Ihre blaue Prognoselinie geht sehr steil nach unten, mit einer schwachen Bewegung einer ähnlichen Variante...
Hier ist gerade diese Variante gephotoshopt und es fiel nicht so steil und mehr logisch von Idee.
Ich habe es bemerkt :) in bestimmten Situationen wird der Winkel aus irgendeinem Grund nicht korrekt gezählt, es begann, als ich es von einer Version mit einem Zeitrahmen zu einer Version mit mehreren Zeitrahmen umgeschrieben habe, und ich habe immer noch nicht herausgefunden, wo der Fehler liegt
Übrigens ist es möglich, dass ich es gar nicht richtig gezählt habe... Ich habe nicht daran gedacht, es mit Photoshop zu überprüfen. Der Winkel zwischen den vorangegangenen Diagrammen und den Prognosen sollte derselbe sein
Ganz genau.
Man kollabiert das Muster und die Reihe, in der die Extreme am ähnlichsten waren, ganz einfach. Wenn Sie zum Beispiel eine Reihe {0,0,0,1,2,3,1,1,1} haben und darin ein Muster {1,2,3} finden wollen, liefert Ihnen die Faltung {0,0,0,3,8,14,11,8, 6} (nach Augenmaß gezählt) höchstens 14, wo der "Kopf" unseres Musters liegt. Natürlich ist es wünschenswert, die Vektoren vor der Faltung zu normalisieren, da es sonst an Stellen mit großen Zahlen zu Extremwerten kommt.
Warum die Dinge so kompliziert machen? Warum sollten wir nach einem Extremum auf der Faltung suchen, wenn wir {0,0,0,1,2,3,1,1,1,1} speziell in der Zeile {1,2,3} suchen können? Abgesehen von der Erhöhung der Komplexität und der Berechnungszeit sehe ich keinen Vorteil.
Warum sollte man die Dinge so kompliziert machen? Warum sollten wir nach einem Extremum auf der Faltung suchen, wenn wir {0,0,0,1,2,3,1,1,1,1} speziell in der Reihe {1,2,3} suchen können? Abgesehen von der Kompliziertheit und der längeren Berechnungszeit sehe ich keine Vorteile.
Hmmm... was meinen Sie mit "gezielt suchen"? Bitte nennen Sie mir ein Beispiel für einen schnelleren Algorithmus als die Faltung.
Zwei Operationen können verwendet werden: Vektor-Differenzlänge und Skalarprodukt, Differenzlänge, glauben Sie mir, ist 3-10 mal langsamer, Komponentendifferenz, Quadrieren, Summe, Wurzelziehen, und Faltung ist zu multiplizieren und zu addieren.
Du musst jedes Stück einer Reihe der Länge 3 als Vektor nehmen und es auf "Ähnlichkeit" mit unserem {1,2,3} vergleichen
Hmmm... was meinen Sie mit "gezielt suchen"? Bitte nennen Sie mir ein Beispiel für einen schnelleren Algorithmus als die Faltung.
Am einfachsten ist es, die Fensterbreite des gesuchten Beispiels schrittweise über die Sequenz zu verschieben und die Summe der abs. Werte der Deltas zu ermitteln:
0,0,0 und 1,2,3 Fehler = (1-0)+(2-0)+(3-0)=6
0,0,1 und 1,2,3 Fehler = (1-0)+(2-0)+(3-1)=5
0,1,2 und 1,2,3 Fehler = (1-0)+(2-1)+(3-2)=3
1,2,3 und 1,2,3 Fehler = (1-1)+(2-2)+(3-3)=0
2,3,1 und 1,2,3 Fehler = (2-1)+(3-2)+Abs(1-3) =4
Wobei der minimale Fehler die maximale Ähnlichkeit ist.
Bemerkt :) in bestimmten Situationen, aus irgendeinem Grund zählt es den Winkel nicht richtig, es begann, nachdem ich von der Version mit einem Zeitrahmen auf die Version mit mehreren Zeitrahmen umgeschrieben habe, und ich habe nie herausgefunden, wo der Fehler liegt
Übrigens ist es möglich, dass ich überhaupt falsch gezählt habe... Ich habe es nicht geschafft, das mit Photoshop zu überprüfen. Ich sollte den gleichen Winkel zwischen den früheren Diagrammen und den Prognosen erhalten.
Ich bin mir noch nicht sicher, ob es richtig ist, Graphen mit einem so großen Unterschied in den Neigungswinkeln als ähnlich zu betrachten. Das gleiche Beispiel:
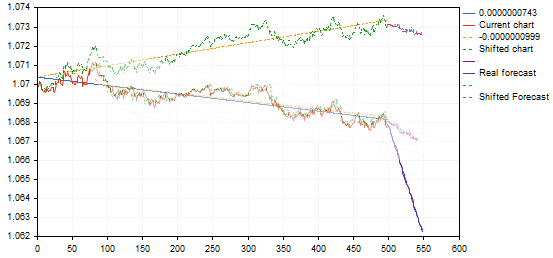
die gefundene Variante einen Pullback vom oberen Trendpunkt oder das Ende des Trends anzeigt, ergibt sich durch die Übertragung auf das Musterdiagramm eine Vorhersage für eine Fortsetzung des rückläufigen Trends und nicht für eine Umkehrung - im Wesentlichen ein Umkehrsignal. Irgendetwas stimmt hier nicht.... vielleicht brauchen wir diese affinen Transformationen nicht....? Und eine einfache Korrelation (minimaler Fehler) ist ausreichend?