Aslında soru şu: Sonuçlar nasıl doğru bir şekilde değerlendirilir?
Her modülün hatası yüzde olarak verilmiştir. %0 ideal sonuçtur.
| ________________ SEÇENEKLER ________________ | Mod 1 | Mod 2 | Mod 3 | Mod 4 | Mod 5 | Mod 6 | Mod 7 | Mod 8 | Mod 9 | Mod 10 | Mod 11 | Mod 12 | 13 Modu | Mod 14 | mod 15 | Ortalama hata | girişimlerin |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND | 4.43 | 17.09 | 15.82 | 2.53 | 0.63 | 17.72 | 28.48 | 5.70 | 13.29 | 5.70 | 8.23 | 6.33 | 0.63 | 3.16 | 6.96 | 9.11 | 158.00 |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1 | 5.06 | 17.72 | 12.66 | 3.80 | 0.63 | 19.62 | 29.11 | 4.43 | 9.49 | 5.06 | 6.33 | 6.33 | 1.90 | 1.90 | 6.33 | 8.69 | 158.00 |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2 | 4.43 | 20.25 | 16.46 | 4.43 | 0.63 | 17.72 | 29.75 | 6.33 | 5.06 | 8.23 | 10.13 | 5.06 | 0.63 | 1.27 | 4.43 | 8.99 | 158.00 |
Her modülün hatasının minimum olmasını, aynı zamanda yayılmanın da minimum olmasını istiyorum.
logaritmaların çarpımı
Not: Tam olarak neyin gerekli olduğunu tam olarak anlamadım, ancak logaritma hataları aşamalı olarak düzeltmenize izin verecek, bu izole durumlarda (bireysel modüller) daha iyi sonuçlar verecektir. Ve çarpma, yayılmayı azaltma girişimidir.logaritmaların çarpımı
Not: Tam olarak neyin gerekli olduğunu tam olarak anlamadım, ancak logaritma hataları aşamalı olarak düzeltmenize izin verecek, bu izole durumlarda (bireysel modüller) daha iyi sonuçlar verecektir. Ve çarpma, yayılmayı azaltma girişimidir.Teşekkür ederim. pratik olarak nasıldır?
Teşekkür ederim. pratik olarak nasıldır?
Belki sadece bir iş gidecek
Variant1 ) Her modülü stile (%1-x) çevirmeye ve bunları çarpmaya değer ..... ortaya çıkan cevap da birden çıkarılır.
burada %x hücrenin değeridir
Seçenek 2
Logaritmalarla, sadece hücrenin değerini alıyoruz ve ondan logaritmayı hesaplıyoruz))) değer sıfıra ne kadar yakınsa, tahminin aşamalılığı o kadar yüksek olur, yani. Belirli bir taban ayarı ile 0.1, 0.01'den daha iyi olacaktır, tıpkı 0.1'in 1'den daha iyi olması gibi.
Belki sadece bir iş gidecek
Variant1 ) Her modülü stile (%1-x) çevirmeye ve bunları çarpmaya değer ..... ortaya çıkan cevap da birden çıkarılır.
burada %x hücrenin değeridir
Seçenek 2
Logaritmalarla, sadece hücrenin değerini alıyoruz ve ondan logaritmayı hesaplıyoruz))) değer sıfıra ne kadar yakınsa, tahminin aşamalılığı o kadar yüksek olur, yani. Belirli bir taban ayarı ile 0.1, 0.01'den daha iyi olacaktır, tıpkı 0.1'in 1'den daha iyi olması gibi.
seçenek 1
| -3.43 | -16.09 | -14.82 | -1.53 | 0.37 | -16.72 | -27.48 | -4.70 | -12.29 | -4.70 | -7.23 | -5.33 | 0.37 | -2.16 | -5.96 | 10601305851,38 |
| -4.06 | -16.72 | -11.66 | -2.80 | 0.37 | -18.62 | -28.11 | -3.43 | -8.49 | -4.06 | -5.33 | -5.33 | -0.90 | -0.90 | -5.33 | -6223799946.09 |
| -3.43 | -19.25 | -15.46 | -3.43 | 0.37 | -16.72 | -28.75 | -5.33 | -4.06 | -7.23 | -9.13 | -4.06 | 0.37 | -0.27 | -3.43 | 1237520122.21 |
Bu bana ne anlatıyor?
seçenek 2
| -0.64640373 | -1.23274206 | -1.19920648 | -0.40312052 | 0,200659451 | -1.24846372 | -1.45453998 | -0.75587486 | -1.12352498 | -0.75587486 | -0.91539984 | -0.80140371 | 0,200659451 | -0.49968708 | -0.84260924 |
| -0.70415052 | -1.24846372 | -1.10243371 | -0.5797836 | 0,200659451 | -1.292699 | -1.46404221 | -0.64640373 | -0.97726621 | -0.70415052 | -0.80140371 | -0.80140371 | -0.2787536 | -0.2787536 | -0.80140371 |
| -0.64640373 | -1.30642503 | -1.21642983 | -0.64640373 | 0,200659451 | -1.24846372 | -1.47348697 | -0.80140371 | -0.70415052 | -0.91539984 | -1.00560945 | -0.70415052 | 0,200659451 | -0.10380372 | -0.64640373 |
Bu, 0.1 tabanlı bir logaritmadır.
Bununla ne yapmalı?
Diğer işlevleri denedim. Ama bunlar nasıl anlaşılmalı? ....
| STDEV | 7.8208 |
| 7.9133 | |
| 8.4150 | |
| EKRAN | 61.1650 |
| 62.6198 | |
| 70.8128 | |
| DÖRTLÜ | 856.3093 |
| 876.6772 | |
| 991.3799 | |
| MEDYAN | 6.3300 |
| 6.3300 | |
| 5.0600 | |
| SKOS | 1.1805 |
| 1.5197 | |
| 1.3018 | |
| AŞIRI | 1.1322 |
| 1.9702 | |
| 1.1832 |
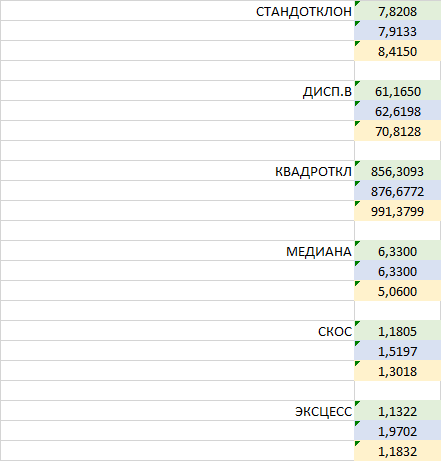
Her satırdamaksimumu bulun , ardından minimum maksimuma sahip satırı seçin. kelime oyunu için özür dilerim))
3. satırdaki maksimum maksimum, ilk satırdaki minimum maksimum. VE? )))
3. satırdaki maksimum maksimum, ilk satırdaki minimum maksimum. VE? )))
İlk satırı seçin.
seçenek 1
| -3.43 | -16.09 | -14.82 | -1.53 | 0.37 | -16.72 | -27.48 | -4.70 | -12.29 | -4.70 | -7.23 | -5.33 | 0.37 | -2.16 | -5.96 | 10601305851,38 |
| -4.06 | -16.72 | -11.66 | -2.80 | 0.37 | -18.62 | -28.11 | -3.43 | -8.49 | -4.06 | -5.33 | -5.33 | -0.90 | -0.90 | -5.33 | -6223799946.09 |
| -3.43 | -19.25 | -15.46 | -3.43 | 0.37 | -16.72 | -28.75 | -5.33 | -4.06 | -7.23 | -9.13 | -4.06 | 0.37 | -0.27 | -3.43 | 1237520122.21 |
Bu bana ne anlatıyor?
seçenek 2
| -0.64640373 | -1.23274206 | -1.19920648 | -0.40312052 | 0,200659451 | -1.24846372 | -1.45453998 | -0.75587486 | -1.12352498 | -0.75587486 | -0.91539984 | -0.80140371 | 0,200659451 | -0.49968708 | -0.84260924 |
| -0.70415052 | -1.24846372 | -1.10243371 | -0.5797836 | 0,200659451 | -1.292699 | -1.46404221 | -0.64640373 | -0.97726621 | -0.70415052 | -0.80140371 | -0.80140371 | -0.2787536 | -0.2787536 | -0.80140371 |
| -0.64640373 | -1.30642503 | -1.21642983 | -0.64640373 | 0,200659451 | -1.24846372 | -1.47348697 | -0.80140371 | -0.70415052 | -0.91539984 | -1.00560945 | -0.70415052 | 0,200659451 | -0.10380372 | -0.64640373 |
Bu, 0.1 tabanlı bir logaritmadır.
Bununla ne yapmalı?
Diğer işlevleri denedim. Ama bunlar nasıl anlaşılmalı?
Hava sıcak." Her modülün hatası yüzde olarak verilmiştir. İdeal sonuç %0'dır." 1 numara %100 - %x veya 1-X * 0.01 anlamına geliyordu

| TOPLAM | ||||||||||||||||
| 0.9557 | 0,8291 | 0.8418 | 0.9747 | 0.9937 | 0.8228 | 0.7152 | 0,943 | 0.8671 | 0,943 | 0.9177 | 0.9367 | 0.9937 | 0.9684 | 0.9304 | 0.77439 | |
| 0.9494 | 0.8228 | 0.8734 | 0,962 | 0.9937 | 0.8038 | 0.7089 | 0.9557 | 0.9051 | 0.9494 | 0.9367 | 0.9367 | 0.981 | 0.981 | 0.9367 | 0.758606 | |
| 0.9557 | 0.7975 | 0,8354 | 0.9557 | 0.9937 | 0.8228 | 0.7025 | 0.9367 | 0.9494 | 0.9177 | 0.8987 | 0.9494 | 0.9937 | 0.9873 | 0.9557 | 0.771806 |
buna dayanarak, en iyi ikinci satır ve birinci ve üçüncü çok benzer
toplam birimden çıkarıldı, yani. sonuç 0'a ne kadar yakınsa, sonuçlar o kadar iyi ..... başka bir deyişle, şu ana kadar sonuçlar çok iyi değil. 0,75 sizin 75'inizdir, ancak neyle karşılaştırılacağınıza bağlı olarak ..... olası en kötü puan 1 (%100) mümkün olan en iyi 0 olacaktır.
90 puanın 99 puandan on kat daha iyi olduğu anlaşılmalıdır .... 99 puan 99.9 puandan on kat daha iyidir ... 100 sayısı aslında ancak tüm modüller olduğunda mümkündür 100'lük bir hata puanı ... ayrıca adil ve diğer tarafta. onlar. 0,1 puan, 0,01 puandan on kat daha kötüdür. 10 puan, 1 puandan on kat daha kötüdür.
düşünmek için bir logaritma ile ..... cevap yalnızca pozitif değerler olmalıdır ... genellikle 1.1 ... logaritmasını 1 ile 2 arasında alırlar ve 0 ile 1 arasında değil ... . sayıyı artırmak istiyorlarsa ve sırasıyla 2'den kademeli olarak azaltmak istiyorlarsa
İkinci dereceden sapma yöntemi kesinlikle konu değil. Sapmaları dikkate alan diğerlerinin yanı sıra. Çünkü ideal olarak, yayılmadaki farkı anlamak için doğrusal regresyondan sapmanın karesi kullanılmalıdır. Ama sonra, sayıların kendilerinin herhangi bir ortalama göstergesi olmadan bu sapmaların bir tahminini elde ederiz .....
Aslında soru şu: Sonuçlar nasıl doğru bir şekilde değerlendirilir?
Her modülün hatası yüzde olarak verilmiştir. %0 ideal sonuçtur.
| ________________ SEÇENEKLER ________________ | Mod 1 | Mod 2 | Mod 3 | Mod 4 | Mod 5 | Mod 6 | Mod 7 | Mod 8 | Mod 9 | Mod 10 | Mod 11 | Mod 12 | 13 Modu | Mod 14 | mod 15 | Ortalama hata | girişimlerin |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND | 4.43 | 17.09 | 15.82 | 2.53 | 0.63 | 17.72 | 28.48 | 5.70 | 13.29 | 5.70 | 8.23 | 6.33 | 0.63 | 3.16 | 6.96 | 9.11 | 158.00 |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1 | 5.06 | 17.72 | 12.66 | 3.80 | 0.63 | 19.62 | 29.11 | 4.43 | 9.49 | 5.06 | 6.33 | 6.33 | 1.90 | 1.90 | 6.33 | 8.69 | 158.00 |
| 2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2 | 4.43 | 20.25 | 16.46 | 4.43 | 0.63 | 17.72 | 29.75 | 6.33 | 5.06 | 8.23 | 10.13 | 5.06 | 0.63 | 1.27 | 4.43 | 8.99 | 158.00 |
Her modülün hatasının minimum olmasını, aynı zamanda yayılmanın da minimum olmasını istiyorum.
Modül hatalarının karelerinin toplamını almak ve kökünü almak muhtemelen daha iyidir.
Böylece, modül hatalarının genel bir tahminini elde ederiz.
Değer sıfıra ne kadar yakınsa o kadar iyidir.
Bunun gibi bir şey.
//+------------------------------------------------------------------+ //| EstimateError.mq5 | //| Copyright 2020, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2020, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" double ModN[ 15 ][ 3 ] = {{ 4.43 , 5.06 , 4.43 }, { 17.09 , 17.72 , 20.25 }, { 15.82 , 12.66 , 16.46 }, { 2.53 , 3.80 , 4.43 }, { 0.63 , 0.63 , 0.63 }, { 17.72 , 19.62 , 17.72 }, { 28.48 , 29.11 , 29.75 }, { 5.70 , 4.43 , 6.33 }, { 13.29 , 9.49 , 5.06 }, { 5.70 , 5.06 , 8.23 }, { 8.23 , 6.33 , 10.13 }, { 6.33 , 6.33 , 5.06 }, { 0.63 , 6.33 , 0.63 }, { 3.16 , 1.90 , 1.27 }, { 6.96 , 6.33 , 4.43 }}; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart () { double ModX[]; ArrayResize (ModX, 3 ); ZeroMemory (ModX); int num = 1 ; double est = 0.0 ; for ( int i= 0 ; i< 15 ; i++) { for ( int j= 0 ; j< 3 ; j++) { ModX[j] = ModN[i][j]; } est = EstimateError(ModX); PrintFormat ( "Mod" +( string )num+ " EstimateError: %.3f" , est); num++; } } // End OnStart //+------------------------------------------------------------------+ double EstimateError( double & arr[]) { int size = ArraySize (arr); if (size == 0 || size < 3 ) return ( 0.0 ); //double avg = ArrayMean(arr); double max = ArrayMax(arr); double min = ArrayMin(arr); double sum_sqr_e = 0.0 ; double est_e = 0.0 ; for ( int i= 0 ; i<size; i++) sum_sqr_e += MathPow (arr[i] - (max-min) /* или avg*/ , 2.0 ) / (size - 2.0 ); est_e = MathSqrt (sum_sqr_e); return (est_e); } //+------------------------------------------------------------------- //Возвращает максимальное значение элементов массива double ArrayMax( double & arrIn[]) { uint size = ArraySize (arrIn); if (size == 0 ) return ( 0.0 ); double max = arrIn[ 0 ]; for ( uint i= 1 ; i<size; i++) if (arrIn[i] > max) max = arrIn[i]; return (max); } //-------------------------------------------------------------------- //Возвращает минимальное значение элементов массива double ArrayMin( double & arrIn[]) { uint size = ArraySize (arrIn); if (size == 0 ) return ( 0.0 ); double min = arrIn[ 0 ]; for ( uint i= 1 ; i<size; i++) if (arrIn[i] < min) min = arrIn[i]; return (min); } //-------------------------------------------------------------------- //Возвращает средне арефметическое значение элементов массива double ArrayMean( double & arrIn[]) { uint size = ArraySize (arrIn); if (size == 0 ) return ( 0.0 ); double sum = 0.0 ; for ( uint i= 0 ; i<size; i++) sum += arrIn[i]; return (sum/size); } //--------------------------------------------------------------------
2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod1 EstimateError: 6.965 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod2 EstimateError: 26.422 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod3 EstimateError: 19.577 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod4 EstimateError: 3.226 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod5 EstimateError: 1.091 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod6 EstimateError: 28.540 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod7 EstimateError: 48.234 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod8 EstimateError: 6.361 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod9 EstimateError: 6.102 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod10 EstimateError: 5.965 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod11 EstimateError: 8.130 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod12 EstimateError: 8.098 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod13 EstimateError: 7.198 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod14 EstimateError: 1.413 2020.06 . 07 04 : 59 : 23.227 EstimateError (AUDUSD,M5) Mod15 EstimateError: 6.138
Skor, Mod5'in en küçük hataya sahip olduğunu gösteriyor.
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Aslında soru şu: Sonuçlar nasıl doğru bir şekilde değerlendirilir?
Her modülün hatası yüzde olarak verilmiştir. %0 ideal sonuçtur.
Her modülün hatasının minimum olmasını, aynı zamanda yayılmanın da minimum olmasını istiyorum.