Alım-satım fırsatlarını kaçırıyorsunuz:
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Kayıt
Giriş yap
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Hesabınız yoksa, lütfen kaydolun
TAMAM. İşte veriler.Birbirimizi yanlış anlıyor gibiyiz. Anormallikle ilgili özdeyişlerim üreticiye değil, piyasaya atıfta bulunur. İlk artışların dağılımını oluşturun ve emin olun.
Vakumdaki küresel bir at için, yani. garantili bir normal dağılım için, evet, olası değil. Yani gerçek getiriler, boşluktaki atlar değildir. Ortak vardır ve 5 ve 6 s.k.o. ve hatta 10 vardır.
Amca, sana yalvarırım, işte 1971'den sterlin yanında başka bir fotoğraf, yaz saati uygulaması. Tek bir hamle olabilir (ve bu arada hiçbiri yok :), en önemli şey bunun bir kalıp haline gelmemesidir. Böyle?
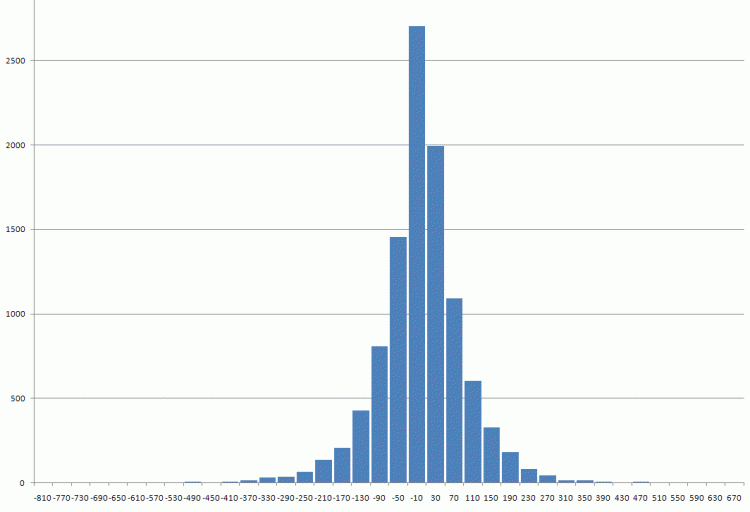
Doğrulama verileri ektedir.1971'den beri ilk pound farkları
not. Belki durağanlık için kontrol edin :)
Amca, sana yalvarırım, işte 1971'den sterlin yanında başka bir fotoğraf, yaz saati uygulaması. Tek bir hamle olabilir (ve bu arada hiçbiri yok :), en önemli şey bunun bir kalıp haline gelmemesidir. Böyle?
Doğrulama verileri ektedir.1971'den beri ilk pound farkları
Ben buna gözle Laplace dağılımı derdim.
Ben buna gözle Laplace dağılımı derdim.
Anahtar, 5-6-10 sigma olmamasıdır. Evet, ama test edilmesi gerekiyor. Ve yine de normal olabilir.İlya , bir öneri var: al ve bu dağılımı normal bir dağılımla tahmin et. Ve sonra gerçek histogramın ve Gauss eğrisinin yaklaşımının birbirinden ne kadar farklı olduğuna bakın. Kendinizi sadece üç sigma ile sınırlamayın, en az on sigmaya bakın.
Başka bir önemsiz test: Bu dağılımın ilk anlarını hesaplayın ve bunları normal dağılımın anlarıyla karşılaştırın.
Finansal serilerdeki yağ kuyrukları olgusu uzun zamandır bilinmektedir. Bana neyi kanıtlamak istiyorsun?
İlya, bir öneri var: bu dağılımı al ve normal bir dağılımla yaklaştır. Ve sonra gerçek histogramın ve Gauss eğrisinin yaklaşımının birbirinden ne kadar farklı olduğuna bakın. Kendinizi sadece üç sigma ile sınırlamayın, en az on sigmaya bakın.
Başka bir önemsiz test: Bu dağılımın ilk anlarını hesaplayın ve bunları normal dağılımın anlarıyla karşılaştırın.
Finansal serilerdeki yağ kuyrukları olgusu uzun zamandır bilinmektedir. Bana neyi kanıtlamak istiyorsun?
Görüşme yaklaşık 5-6-10 RMS oldu. Görünüşlerinde herhangi bir düzenlilik görmüyorum.
Anahtar, 5-6-10 sigma olmamasıdır. Evet, ama test edilmesi gerekiyor. Ve yine de normal olabilir.sadece olası değil. Normal dağılımlar, bir kural olarak, "büyük" bir rastgele değişkenin, bir şekilde (ancak eşit olarak) dağıtılan çok sayıda "küçük" rastgele değişkenin toplamı olduğu doğada meydana gelir. Canlı bir örnek, bir sonraki dalda birçok sayfanın ayrılmış olduğu Brown hareketidir. Piyasa söz konusu olduğunda, fiyat oluşumu yasası bundan uzaktır, çünkü normal bir tane elde etmek için çok büyük miktarda dış "gürültü" gerekir - ki bu da dağıtımın oluşumunda ana faktör olmalıdır. Ancak piyasa fiyatlandırmasının gürültü olduğunu düşünmüyoruz, değil mi?
Grafikte tamamen görsel olarak bunları 5-6-10 görmeyeceksiniz.
Bir yerde farklılıkları gösteren bir işaret bile vardı. Dağılımın ilk iki anını alırsak ve bunları yaklaşık normalin anları olarak kabul edersek, frekanslardaki fark 3, 4, 5, vb. sigmanın hesaplanması kolaydır.
Tam sayıları hatırlamıyorum, ancak gerçek sapma frekansı 3 sigma çarpı 3-4 kat daha fazla Gauss (Gauss'a göre -% 0,3, gerçekte -% 1'den fazla). Gerçek hayatta 4 sigma sapması Gauss sapmasından yaklaşık 15 kat daha sık meydana gelir.5 sigma için fark yüzlerce değilse de onlarca kattır. Vb.
Riskleri değerlendirmediğiniz sürece Gauss olup olmaması umurunuzda değil.
PS Bu arada, Taleb'e göre, LTCM'nin tam olarak risklerin hafife alınması nedeniyle çöktüğü ortaya çıktı. 10 sigma sapması ihmal edilebilir bir olay olarak kabul edildi. Ve sadece oldu.
Tam sayıları hatırlamıyorum, ancak gerçek sapma frekansı 3 sigma çarpı 3-4 kat daha fazla Gauss (Gauss'a göre -% 0,3, gerçekte -% 1'den fazla). 4 sigma sapma gerçek hayatta bir Gauss sapmasından yaklaşık 15 kat daha sık meydana gelir.5 sigma için fark onlarca kattır. Vb.
... bu bir kez daha Laplace lehine tanıklık ediyor
Riskleri değerlendirmediğiniz sürece Gauss olup olmaması umurunuzda değil.
Risk değerlendirmesine nasıl yaklaşmamız gerektiğini anlatır mısınız?