Alım-satım fırsatlarını kaçırıyorsunuz:
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Kayıt
Giriş yap
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Hesabınız yoksa, lütfen kaydolun
Hayır, çalışmıyor. Bu formüle göre, BGN'nin korelasyonlu olduğu ortaya çıkıyor. Her zaman r eksi 0,5 civarındadır
İşte doğrulama kodu
Kontrol.
Sergey, doğru yapalım.
1. Alıntıya benzer şekilde BP ile çalışıyoruz. Böyle bir seri, SW'yi sıfır MO ile entegre ederek elde edilir. Sıfır MO'lu bir CB örneği:
dX=rnorm(n+1,0,10), burada n+1, Gauss dağılımına sahip CV üyelerinin sayısıdır, 0, benim durumumda sıfıra eşit MO'dur ve sizin örneğinizde 10, genişliktir bu dağılımın benim durumumda ve 100 - sizinkinde. Fiyatına benzer bir VR oluşturmak için orijinal seriyi entegre etmeliyiz (kümülatif toplamını bulun):
Entegre yazılımın artışlarının dağılımları (soldaki şekil) ve artışların kendilerinin VR arka planına karşı nasıl göründüğü (sağdaki şekilde kırmızı ve mavi çizgiler):
Sergey, şu anda incelediğimiz VR'nin (mavi olan) özellikleridir ve yazınızda ilk fark, ilk fark (dX içinde dX) serisindeki korelasyon katsayısını hesaplama formülünü değiştirdiniz. benim notasyonum ve sizinkinde X). Tabii ki, R=0.5 alacaksınız ve başka bir tane olmamalıdır (temel olduğu kanıtlanmıştır). Yani, şimdi sıfır MO'lu (sağdaki şekilde mavi olan) entegre bir SW için önerdiğim formülü kullanarak r'yi hesaplarsanız, beklenen sıfırı alırsınız:
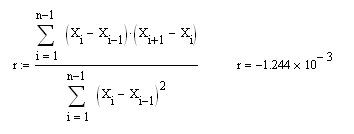
Ve elbette, bu, bir dizi dX artışı için r ile aynıdır (ancak farklı bir formülde):
Umarım şimdi bu noktada bir fikir birliğine varırız?
Not: Bunu da yapabilirsiniz:
Tamam, sırayla gidelim.
Söylediğinizi yaptım, entegre CB ile POI = 0. İşte kodun tamamı
İlk bakışta her şey yolunda gibi görünüyor. Ama bir tuzak var. Formüle girdi olarak ilişkili bir dizi kullanalım. Trend + gürültü şeklinde. y=a*x+b+rnorm(). Bu, basitçe POI = 0 ayarlanarak yapılabilir, diyelim ki 0,5
Şekilden, eğrinin (mavi) açıkça ilişkili olduğu görülebilir. A ve B olmak üzere iki diziye bölerek korelasyon katsayısını hesaplıyoruz, 0.993 olduğu ortaya çıkıyor. Ve formülünüze göre 0.225.
Gerçek şu ki, tanım gereği korelasyon katsayısı (KK) iki dizi arasında kabul edilir. Aynısını kullanıyorsun. Böylece diziyi kendisiyle karşılaştırmak için yapabilirsiniz. Buna ACF denir, yani. iki dizi A oluşturulur, orijinal olan ve ikincisi B, A'ya göre zaman içinde kaydırılır ve bir grafik çizilir - QC'nin kaymaya bağımlılığı. Kayma yoksa, QC doğal olarak = 1. İşte son mavi eğrinin ACF grafiği.
Uygulama bu şekilde ortaya çıktı. Onlar. Ben kendi fikrimle kalırken, bu formüle göre bir şey düşündüğünüzü, ancak bu QC değil. Rakamlar eşleşmiyor
Ama yoldan çıktık. Önce Hurst'u doğru bir şekilde hesaplamalı ve ancak o zaman KK'den nasıl farklı olduğuna bakmalısınız.
İşte çeşitli zaman serilerinin analizinin yapıldığı ilginç bir çalışma.
Hurst üssünü kullanarak.
Şekilden, eğrinin (mavi) açıkça ilişkili olduğu görülebilir. A ve B olmak üzere iki diziye bölerek korelasyon katsayısını hesaplıyoruz, 0.993 olduğu ortaya çıkıyor. Ve formülünüze göre 0.225.
Burada tam olarak anlamadım.
Modaya uygun VR'yi hangi dizilere böldünüz? Y=a*X+b satırında ve sıfır MO'lu rastgele bir bileşen ve aralarında bir korelasyon katsayısı mı arıyorsunuz?
İşte çeşitli zaman serilerinin analizinin yapıldığı ilginç bir çalışma.
Hurst üssünü kullanarak.
Burada tam olarak anlamadım.
Şimdi anladım.
Orijinal BP (artışları değil) ile aynısı arasındaki korelasyon katsayısını arıyorsunuz, ancak 500 sayı sağa kaydırıldı. Onlar. iki daima pozitif BP arasındaki korelasyon katsayısını arıyor! Tabii ki her zaman pozitif ve çok büyük (yaklaşık 1) olacaktır.
Sergey, seni anlamıyorum! Ne düşünüyorsunuz, orijinal VR ile aynı ancak değişmiş arasındaki korelasyon katsayısı mı? Nafik ona ihtiyacımız var mı?! İlk VR'nin ilk farkı serisindeki bitişik okumalar arasındaki korelasyon katsayısıyla ilgileniyoruz. Beklenen artışın öncekilere bağımlılığını gösteren kişidir. 1/2 kaydırılan Hurst ile aynı olan bu indekstir.
Teşekkür ederim. Göreceğiz.
Burada gerçek gibi görünüyor.
Uygulamaya çalıştım ama kurslar için 1'e çok yaklaştım.
______________
Makaleyi tekrar okudum - bir komisyona basmış gibi görünüyor.
Döviz çiftleri için türev için Hurst üssü, döviz kuru için I hesaplanmalıdır.
Makaleyi tekrar okudum - bir komisyona basmış gibi görünüyor.
mda :-)
Önden koşmak.
Entegre CB ve EURGBP oranı serisi bu şekilde görünür (soldaki şekil) ve farklı zaman dilimlerindeki artışlarının genlikleri çift logaritmik ölçekte şöyle görünür (sağdaki şekil) , TF'nin logaritması apsis boyunca çizilir:
Hers, bu çizgilerin eğiminin tanjantının, rastgele bir entegre değer için 1/2 (böyle bir fiyat üzerinden işlem yapmak mantıklı değil), bir geri çekilme piyasası için 1/2'den küçük ve 1/2'den fazla olduğunu savunuyor. trend olan biri. Bakalım bu açı SW için neymiş. Burada, makalede önerildiği gibi, bir LSM düz çizgisi çizebilir ve eğimini bulabilirsiniz, ancak bu değeri yerel olarak bulacağım - her iki noktadan bir düz çizgi çizerek. Sonuç olarak, her bir TF için RH'yi elde ederiz:
Burada, daireler NE (kırmızı renk) için RP'yi ve mavi olarak gösterir - EURGBP teklifi için, dakika cinsinden TF apsis boyunca çizilir. Çaprazlar, orijinal serinin birinci farkının 1/2'lik bir kayma ile serileri için bitişik okumalar arasındaki korelasyon katsayısını gösterir. Korelasyon katsayısı bu sayfanın ilk mesajında verilen formüle göre bulunmuştur. VR'nin öngörülebilirliğini değerlendirmek için bu iki yöntem arasındaki anlaşmanın tatmin edici olduğu görülebilir, oysa benim durumumda çok daha az formül var (sadece bir). Hangi, aslında, gösterilmesi gerekiyordu.
Ayrıca Random serisi tanımdan aşağıdaki gibi HX=1/2 ve r=0 (şekilde ofset vardır) vermiştir. Kotir için bir geri dönüş eğilimi (kalıcılık önleme) açıkça görülebilir, ne kadar büyükse, TF o kadar küçüktür.
Burada, daireler NE (kırmızı renk) için RP'yi ve mavi olarak gösterir - EURGBP teklifi için, dakika cinsinden TF apsis boyunca çizilir.
Rastgele seri, tanımdan aşağıdaki gibi RH=1/2 ve r=0 (şekilde bir sapma vardır) vermiştir. Kotir için bir geri dönüş eğilimi (kalıcılık önleme) açıkça görülebilir, ne kadar büyükse, TF o kadar küçüktür.
Muhtemelen bu yüzden pipers europound'u bu kadar çok seviyor
Muhtemelen bu yüzden pipers europound'u bu kadar çok seviyor
Bu apaçık!
Bu apaçık!
Tamamen meraktan - Son derece kalıcı çiftler bulmak istiyorum,
veya en kötü ihtimalle kalıcılığın meydana geldiği koşullar):