- Постановка задачи
- Структура расположения файлов
- Выбор исходных данных
- Закладываем скелет будущей программы MQL5
- Описание структуры скрипта Python
- Полносвязный нейронный слой
- Организация параллельных вычислений средствами OpenCL
- Реализация модели перцептрона в Python
- Создание обучающей и тестовой выборки
- Проверка корректности распределения градиента
- Сравнительное тестирование реализаций
Сравнительное тестирование реализаций
В предыдущем разделе мы проверили корректность работы алгоритма обратного распространения ошибки. Теперь можно смело переходить к обучению нашего перцептрона. Данную работу мы проведем в скрипте perceptron_test.mq5. Первый блок скрипта напомнит вам скрипт из предыдущего раздела. Это следствие использования нашей библиотеки для создания нейронных сетей. Создавать нейронную сеть мы будем с ее помощью. Следовательно, алгоритм инициализации и использования нейронной сети будет во всех случаях идентичный.
Для возможности проведения различных вариантов тестирования в скрипт добавим нижеследующие внешние параметры:
- Имя файла, содержащего обучающую выборку.
- Имя файла для записи динамики изменения ошибки. По данным значениям мы сможем построить график изменения ошибки в процессе обучения, что поможет нам визуализировать процесс обучения нейронной сети.
- Количество исторических баров, используемых в описании одного паттерна.
- Количество нейронов входного слоя на один бар.
- Флаг-переключатель использования технологии OpenCL в процессе обучения нейронной сети.
- Размер пакета для одной итерации обновления матрицы весов.
- Обучающий коэффициент.
- Количество скрытых слоев.
- Количество нейронов в одном скрытом слое.
- Количество итераций обновления матрицы весов.
Как и в предыдущем разделе, после объявления внешних параметров в глобальной области скрипта подключим нашу библиотеку для создания нейронной сети и объявим объект базового класса CNet.
//+------------------------------------------------------------------+
|
Перед тем как перейти к написанию кода скрипта, давайте подумаем, каким функционалом нам нужно его наполнить.
Вначале нам предстоит создать модель. Для этого мы создадим описание архитектуры модели и вызовем метод инициализации модели. Аналогичные операции мы выполняли в скрипте проверки корректности распределения градиента ошибки.
Затем, чтобы обучить нашу модель, нам необходимо загрузить ранее созданную обучающую выборку, которая будет содержать набор исходных данных и целевых значений.
Лишь после успешного выполнения вышеуказанных операций мы можем запустить процесс обучения модели. Это повторяющийся циклический процесс. Он включает в себя прямой проход, обратный проход и обновление матрицы весов. Есть несколько подходов к продолжительности обучения моделей. Наиболее часто используется ограничение по количеству эпох обучения и контроль изменения ошибки модели. Мы будем использовать первый вариант. Анализ динамики ошибки в процессе обучения модели позволит нам выработать критерии для применения второго метода. Поэтому в процессе обучения нам нужно записать изменение ошибки модели и сохранить собранную последовательность после обучения модели.
Ну и конечно, обучение модели не должно быть «пустой» работой. В конце обучения мы сохраним полученную модель.
Таким образом, мы определили необходимый функционал нашего скрипта. С целью создать понятный и читаемый код, мы разделим его на блоки, аналогичные вышеуказанным задачам. В теле основной функции OnStart лишь будем осуществлять последовательный вызов соответствующих функций с контролем выполнения операций.
Вначале мы создадим вектор для записи динамики ошибки модели в процессе обучения. Его размер будет равен количеству эпох обучения.
//+------------------------------------------------------------------+
|
Затем инициализируем нашу модель для обучения. Здесь мы объявляем экземпляр класса нейронной сети и передадим указатель на объект в функцию инициализации модели. Обязательно проверяем результат выполнения операции.
//--- 1. инициализация модели
|
Следующим шагом загружаем обучающую выборку. Для этого нам потребуется два динамических массива: один из них для загрузки паттернов исходных данных, второй — для целевых значений. Оба массива будут синхронизированы.
Непосредственно загрузка данных осуществляется в функции LoadTrainingData, в параметрах которой мы передадим файл для загрузки данных и указатели на созданные объекты динамических массивов.
//--- 2. загрузка данных обучающей выборки
|
Как и было сказано выше, после создания модели и загрузки обучающей выборки мы можем начать процесс обучения. Данный функционал будет возложен на метод NetworkFit, в параметрах которому мы передадим указатели на нашу модель, обучающую выборку с целевыми значениями и вектор записи динамики изменения ошибки модели в процессе обучения.
//--- 3. обучение модели
|
После завершения процесса обучения модели мы сохраняем историю изменения ошибки модели в процессе обучения. Также сохраним обученную модель. Для сохранения обученной модели нам нет необходимости создавать отдельную функцию, так как в данном случае мы можем воспользоваться ране созданным методом нашего базового класса нейронной сети сохранения модели.
//--- 4. сохранение истории ошибок модели
|
В подтверждение успешного завершения всех операций выведем информационное сообщение в журнал и завершим работу скрипта.
Как можно заметить, код основной функции скрипта получился довольно сжатым, но четко структурированным. Это выгодно отличает его от скрипта проверки корректности распределения градиента в предыдущем разделе. Выбор стиля программирования остается за программистом и не влияет на функциональность нашей библиотеки. Мы же возвращаемся к нашему скрипту и теперь займемся написанием функций, которые выше мы вызывали из основной функции скрипта.
Первой по списку у нас идет функция инициализация модели NetworkInitialize. В параметрах данной функции мы передаем указатель на объект создаваемой модели. В теле функции нам предстоит инициализировать модель перед обучением. Для инициализации модели нам необходимо дать описание создаваемой модели. Напомню, описание модели мы создаем в динамическом массиве, каждый элемент которого содержит указатель на экземпляр объекта CLayerDescription с описанием архитектуры конкретного нейронного слоя. Саму операцию создания подобного описания модели мы вынесли в отдельную функцию CreateLayersDesc, что является естественным продолжением концепции структурированного кода.
//+------------------------------------------------------------------+
|
После создания описания архитектуры модели мы вызываем метод инициализации нашей нейронной сети CNet::Create. В него передаем описание архитектуры модели, коэффициент обучения, параметры оптимизации, функцию потерь и параметры регуляризации. Не забываем проверить результат выполнения операций создания модели.
//--- инициализируем сеть
PrintFormat("Error of init Net: %d", GetLastError());
|
После успешной инициализации модели установим флаг использования технологии OpenCL и размер пакета для усреднения ошибки модели. В приведенном примере последний устанавливается на уровне пакета обновления матрицы весов.
Чтобы завершить описание процесса инициализации модели, предлагаю сразу посмотреть на функцию создания описания архитектуры модели CreateLayersDesc. В параметрах метод получает указатель на динамический массив, в который мы и запишем архитектуру создаваемой модели.
Первым мы создаем описание слоя исходных данных. Количество нейронов во входном слое исходных данных зависит от двух внешних параметров: количества исторических баров в одном паттерне (BarsToLine) и количества нейронов входного слоя на один бар (NeuronsToBar). Определяется количество их произведением. Входной слой будет без функции активации и не будет обучаться. Это вполне понятно и не должно вызывать вопросов, ведь в массив результатов данного слоя мы закладываем исходные параметры из внешней системы, а внутри слоя не осуществляется никаких операций над данными.
bool CreateLayersDesc(CArrayObj &layers)
|
При использовании полносвязных нейронных слоев каждый нейрон скрытого слоя можно рассматривать в качестве определенного паттерна, который нейронная сеть выучит в процессе обучения. В такой логике количество нейронов скрытого слоя представляет собой количество паттернов для запоминания нейронной сетью. Конечно, можно выстроить логическую взаимосвязь между количеством элементов в предыдущем слое и количеством возможных их комбинаций, которые будут представлять паттерны. Но не будем забывать, что наши результаты предыдущего нейронного слоя — небинарные величины, и диапазон их изменения довольно велик. Поэтому полное количество возможных комбинаторных вариантов паттернов получится очень большое. Среднестатистическая вероятность их появления будет сильно отличаться. Поэтому чаще всего количество нейронов в каждом скрытом слое будет определяться архитектором нейронной сети в каком-то диапазоне, а точное количество подбирается по лучшим показателям на валидационной выборке. Именно поэтому мы предоставили пользователю возможность указать количество нейронов в скрытом слое во внешнем параметре HiddenLayer. Но сразу скажем, что мы будем создавать все нейронные слои одинаковой архитектуры и одного размера.
Количество скрытых слоев зависит от сложности решаемой задачи и также определяется архитектором нейронной сети. В данном тесте я буду использовать нейронную сеть с одним скрытым слоем. Но в то же время, я предлагаю вам самостоятельно провести несколько экспериментов с разным количеством слоев и оценить влияния изменения данного параметра на результат. Для проведения таких экспериментов мы вывели отдельный внешний параметр — количество скрытых слоев (HiddenLayers).
На практике мы создаем описание одного скрытого слоя и затем добавляем его в динамический массив описания архитектуры столько раз, сколько нам необходимо создать скрытых нейронных слоев.
//--- скрытый слой
|
В рамках данного раздела я не ставлю целью полное обучение нейронной сети с получением максимально возможных результатов. Мы лишь сравним работу нашей библиотеки в различных режимах и их влияние на результаты обучения. Также посмотрим на практике влияние некоторых подходов, которые мы обсуждали в теоретической части книги. Поэтому мы не будем сейчас сильно останавливаться на тщательном выборе архитектурных параметров нейронной сети для получения максимальных результатов.
В качестве функции активации для скрытого слоя я указал Swish. Это одна из тех функций, диапазон значений которой ограничен снизу и не ограничен сверху. При этом функция дифференцируема на всем протяжении допустимых значений. Но в процессе тестирования мы сможем оценить и другие функции активации.
Выбор функции активации для выходного слоя является компромиссным решением. Дело в том, что у нас есть две цели: направление движения и сила движения. Это не совсем стандартный подход к решению задачи, так как у нас на выходе нейронной сети два нейрона с абсолютно разными значениями. Можно сказать, что у них даже класс значений разный. Если направление движения можно отнести к бинарной классификации (покупка или продажа), то определение силы движения является регрессионной задачей. И, наверное, было бы логично нейронную сеть обучить только на определение силы движения, а направление бы соответствовало знаку результата. Но мы же учимся и экспериментируем. Давайте посмотри на поведение нейронной сети в столь нестандартной ситуации, а активировать нейроны попробуем линейной функцией, как стандартной для решения задач регрессии.
В качестве метода обучения для обоих нейронных слоев я указал Adam.
Алгоритм описания нейронных слоев полностью идентичен рассмотренному в предыдущем разделе. Сначала мы описываем каждый слой в объекте класса CLayerDescription. Последовательность описания слоев соответствует их последовательности в нейронной сети от входного слоя исходных данных до выходного слоя результатов. По мере описания слоев добавляем их в коллекцию ранее созданного динамического массива.
//--- слой результатов
|
Следующим этапом работы нашего скрипта стала загрузка обучающей выборки в функции LoadTrainingData. Загружать мы ее будем из файла, указанного в параметрах функции. В теле функции мы сразу открываем указанный файл для чтения и проверяем результат операции по значению полученного хендла.
//+------------------------------------------------------------------+
|
Операцию загрузки обучающей выборки мы будем осуществлять в два этапа. Сначала поэлементно будем загружать паттерны и целевые значения в два буфера CBufferType. В буфере pattern будем собирать элементы исходных данных одного паттерна, а в буфере target — соответствующие ему целевые результаты.
//--- выводим прогресс загрузки данных обучения в комментарий чарта
|
После загрузки из файла информации одного паттерна сохраним указатели на объекты с данными в два динамических массива CArrayObj. Указатели на них мы также получили в параметрах функции. Один массив используется для паттернов исходных данных (data), а второй — для целевых значений (targets). Операции повторим в цикле до достижения конца файла. Для мониторинга процесса пользователем выведем информацию о количестве загруженных паттернов на график в поле комментариев.
Обратите внимание, что поскольку мы передаем в динамические массивы указатели на объекты с данными, то после записи указателей в массив нам необходимо создать новые экземпляры объектов CBufferType. В противном случае мы заполним весь динамический массив указателем на один и тот же экземпляр объекта, а буфер будет содержать безликую информацию обо всех паттернах, работа с которыми потребует другого алгоритма. Следовательно, вся нейронная сеть будет работать некорректно.
if(!data.Add(pattern))
|
После завершения цикла считывания данных мы получим два массива объектов с одинаковым количеством элементов. В них элементы с одним индексом будут составлять пару «исходные — целевые» данные паттерна. Здесь закрываем файл обучающей выборки.
Теперь, когда у нас уже создана нейронная сеть и загружена обучающая выборка, мы можем приступить к обучению в функции NetworkFit. В параметрах данный метод получает указатели на объекты нейронной сети и обучающей выборки. Также он получает указатель на вектор записи динамики изменения ошибки модели в процессе обучения. Для обучения нейронной сети мы создадим два вложенных цикла. Первый цикл запустим с числом итераций равным внешнему параметру количества обновлений матрицы весов Epochs. Во вложенном цикле создадим число итераций равное размеру пакета для обновления весовых коэффициентов BatchSize.
bool NetworkFit(CNet &net, const CArrayObj &data, |
В теле вложенного цикла будем случайным образом выбирать из обучающей выборки по одному паттерну. Для каждого выбранного паттерна сначала сделаем прямой проход на соответствующих исходных данных. Затем откроем целевые значения и сделаем обратный проход.
//--- выбор случайного паттерна
|
Повторяя итерации прямого и обратного проходов, мы накапливаем градиент ошибки на каждом элементе матрицы весов. После набора числа итераций прямого и обратного проходов до размера пакета для обновления матрицы весов выходим из внутреннего цикла. Обновляем весовые коэффициенты в направлении среднего градиента ошибки. Очищаем буфер накопленных градиентов ошибки. Сохраняем текущее значение функции потерь в вектор для отслеживания процесса обучения. После этого заходим на новый цикл итераций обучения.
//--- перенастраиваем веса сети
|
В предложенном примере процесс обучения ограничивается внешним параметром числа итераций обновления матрицы весов. На практике часто применяется подход, когда процесс обучения прекращается при достижении заданных результатов метрик качества обучения. Это может быть значение функции потерь, доля попаданий в ожидаемые результаты и т.д. А можно применять и гибридный подход, при котором отслеживаются метрики и в тоже время задается максимальное число итераций обучения.
После завершения процесса обучения мы сохраняем в файл динамику изменения функции потерь. Этот функционал выполняется функцией SaveLossHistory, в параметрах которой мы передадим имя файла для записи данных и вектор динамики изменений ошибки модели в процессе обучения.
В теле функции мы открываем или создаем новый CSV-файл для записи данных и в цикле сохраняем все значения ошибки модели в процессе обучения.
void SaveLossHistory(string path, const VECTOR &loss_history)
|
После записи данных в файл закрываем файл и выводим в журнал информационное сообщение с указанием полного пути сохраненного файла.
В рассмотренном примере реализации скрипта показана полная загрузка в память обучающей выборки. Конечно, работа с оперативной памятью всегда быстрее обращения к постоянной памяти. Но не всегда размеры обучающей выборки позволяют ее полностью загрузить в оперативную память. В таких случаях обучающую выборку загружают и обрабатывают частями.
Нормализация данных на входе нейронной сети
После создания такого скрипта мы можем провести несколько поучительных экспериментов. К примеру, ранее мы обсуждали важность нормализации исходных данных перед подачей их на вход нейронной сети. А насколько это важно? Почему в процессе обучения нейронной сети нельзя подобрать подходящие весовые коэффициенты, которые бы учитывали масштаб данных? Да, мы говорили о влиянии больших величин. Но сейчас мы можем провести практический эксперимент и увидеть влияние нормализации исходных данных на результат обучения модели.
Возьмем исторические данные по инструменту EURUSD, пятиминутный таймфрейм за период с 01.01.2015 по 31.12.2020 и создадим две обучающие выборки с нормированными и ненормированными данными. Запустим вышеописанный скрипт обучения нейронной сети на обоих выборках. Скрипт создания обучающей выборки мы создали в разделе 3.9.
График динамики функции потерь более чем красноречив. Ошибка на нормированных данных значительно ниже, даже если мы начинаем со случайными весовыми коэффициентами. Если на ненормированных данных стартовое значение функции потерь около 120, то на нормированных данных оно составляет только 0,6. Конечно, в процессе обучения значение функции потерь на ненормированных данных стремительно падает и после 200 итераций обновления весовых коэффициентов снижается до 6, а после 1000 итераций достигает 4,5. Но несмотря на столь стремительную динамику снижения показателя функции потерь оно все же значительно превосходит показатели для нормированных данных. На последних функция потерь после 1000 итераций обновления матрицы весов приближается к 0.44.
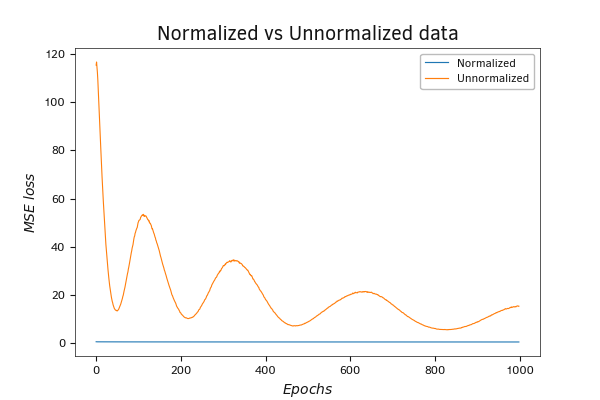
График динамики функции потерь MSE при обучении нейронной сети на нормированных и ненормированных данных
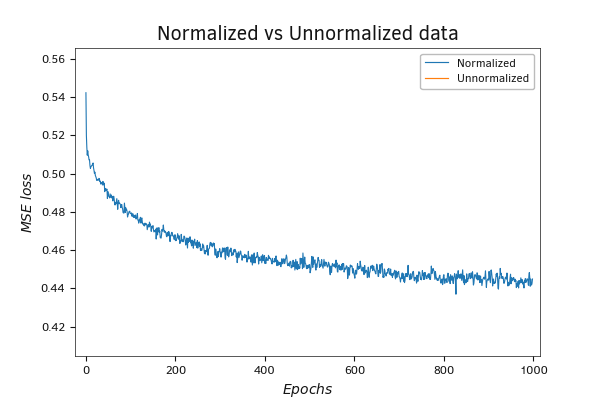
График динамики функции потерь MSE при обучении нейронной сети на нормированных и ненормированных данных (масштаб)
Я провел подобный эксперимент как с использованием технологии OpenCL, так и без. Результаты работы нейронной сети оказались сопоставимыми. А вот по производительности на столь малой нейронной сети выиграла CPU. Очевидно, что накладные расходы на передачу данных оказались значительно выше прироста производительности за счет использования многопоточной технологии. Такие результаты были ожидаемы. Мы уже говорили ранее, что использование подобной технологии оправдано для больших нейронных сетей, когда затраты на передачу данных между устройствами покрываются приростом производительности за счет разделения вычислительных итераций на параллельные потоки.
Я предлагаю вам повторить подобный опыт со своими данными — тогда у вас не останется вопроса о необходимости нормирования исходных данных.
Думаю, после проведенного эксперимента становится очевидным, что дальнейшее тестирование будет проводиться на нормированных данных.
Выбор коэффициента обучения
Следующий вопрос, который всегда становится перед создателями нейронных сетей, — это выбор коэффициента обучения. При решении этой задачи необходимо соблюсти баланс между производительностью и качеством обучения. Выбор заведомо большого коэффициента обучения позволяет быстрее снижать ошибку в начале обучения. Но потом скорость обучения быстро снижается и в лучшем случае останавливается далеко от заведомой цели. В худшем случае ошибка начинает расти. Выбор заведомо малого коэффициента обучения снижает скорость обучения. Процесс занимает больше времени, и при этом повышается риск «застрять» в локальном минимуме, так и не достигнув желаемой цели.
Для экспериментального тестирования влияния скорости обучения на процесс обучения нейронной сети проведем обучение созданной выше нейронной сети при четырех различных коэффициентах обучения: 0,003, 0,0003, 0,00003 и 0,000003. Результаты тестирования представлены на графике ниже.
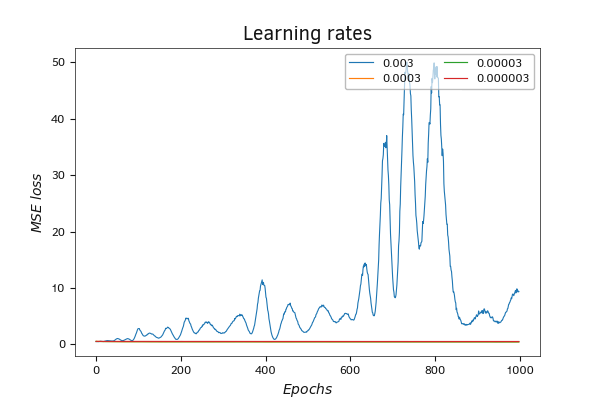
Сравнение динамики функции потерь при использовании разной скорости обучения
При обучении нейронной сети с использованием коэффициента обучения 0,003 наблюдаются колебания функции потерь. В процессе обучения амплитуда колебаний растет. В целом наблюдается тенденция к росту ошибки модели. Такое поведение характерно для завышенного коэффициента обучения.
Снижение коэффициента обучения делает график обучения более плавным. Но при этом снижается и скорость падения значения функции потерь с каждым обновлением матрицы весов. Наиболее ровное снижение значения функции потерь демонстрирует процесс обучения с коэффициентом обучения 0,000003. Но за плавность графика пришлось заплатить ростом количества итераций обновления матрицы весов для достижения оптимального результата. За весь процесс обучения в 1000 итераций обновления матрицы весов коэффициент обучения 0,000003 показал наихудший результат из всех.
Обучение нейронной сети с коэффициентами 0,0003 и 0,00003 показали близкие результаты. График функции потерь при коэффициенте обучения 0,00003 получился более рваный. Но в то же время наилучший результат по значению ошибки показало обучение с коэффициентом 0,0003.
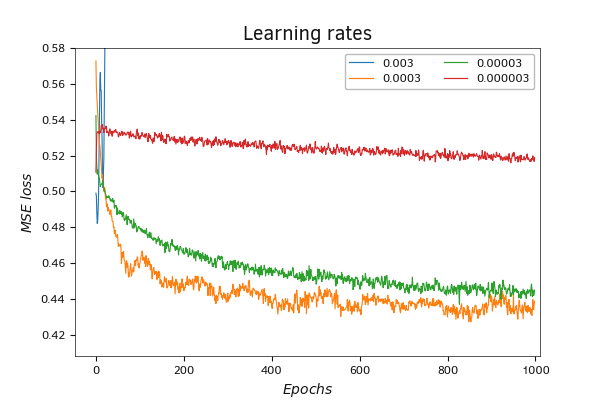
Сравнение динамики функции потерь при использовании разной скорости обучения (масштаб)
Подбор количества нейронов в скрытом слое
Следующий момент, который бы хотелось продемонстрировать на практике — это влияние количества нейронов в скрытом слое на процесс обучения и его результат. Когда мы говорим о полносвязных нейронных слоях, в которых каждый нейрон последующего слоя имеет взаимосвязи со всеми нейронами предыдущего слоя и при этом каждая связь индивидуальна и независима, логично предположить, что каждый нейрон будет активирован своей комбинацией из состояний нейронов предыдущего слоя. Таким образом, каждый нейрон реагирует на свой паттерн состояния предыдущего слоя. Следовательно, наличие большего числа нейронов в скрытом слое потенциально способно запомнить больше таких паттернов и сделать их более детальными. При этом мы не программируем вариации паттернов, а позволяем нейронной сети их выучить самостоятельно из представленной обучающей выборки. Казалось бы, в такой логике увеличение количества нейронов в скрытом слое позволяет только увеличить качество обучения нейронной сети.
Но на практике не все паттерны обладают равной долей вероятности к появлению. Цель обучения нейронной сети не в том, чтобы заучить каждое отдельное состояние до мельчайших подробностей. Их цель — используя обучающую выборку, обобщить представленные в ней данные, найти и выделить зависимости и закономерности. Полученные данные должны позволить построить функцию зависимости целевых значений от исходных данных с требуемой точностью. Поэтому безмерное увеличение нейронов в скрытом слое снижает способность нейронной сети к обобщению и ведет к переобучению нейронной сети.
Вторая сторона вопроса увеличения числа нейронов в скрытом слое — это увеличение затрат временных и вычислительных ресурсов. Дело в том, что добавление одного нейрона в скрытом слое добавляет к матрице весов столько элементов, сколько содержит предыдущий слой плюс один элемент для bias. Следовательно, выбирая количество нейронов в скрытом слое, следует учитывать баланс между получаемым качеством обучения и затратами на обучение такой нейронной сети. В то же время нужно помнить о риске переобучения.
Конечно, существуют выработанные методы борьбы с переобучением нейронных сетей. Это в первую очередь увеличение обучающей выборки и регуляризация. Теоретические аспекты регуляризации мы уже обсуждали ранее, а о практическом использовании поговорим чуть позже.
Сейчас же предлагаю посмотреть на графики значения функции ошибки при обучении нейронной сети с одним скрытым слоем, в котором меняется число нейронов при прочих равных условиях. При тестировании я сравнил процесс обучения 4 нейронных сетей с 20, 40, 60 и 80 нейронами в скрытом слое. Конечно, подобное количество нейронов слишком мало для получения каких-либо достойных результатов обучения на выборке в 350 тыс. паттернов. И тем более здесь нет никакого риска переобучения. Но их достаточно, чтобы посмотреть на влияние данного фактора на процесс обучения.
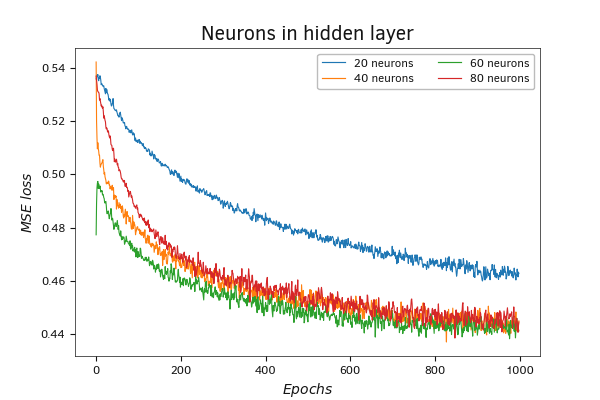
Сравнение динамики функции потерь при использовании разного количества нейронов в скрытом слое
Как можно заметить на графике, наихудший результат показала модель с 20 нейронами в скрытом слое. Их явно недостаточно для решения подобной задачи.
Касательно остальных трех моделей можно сказать, что разброс графиков в первые 100 итераций обновлений весовых коэффициентов можно списать на фактор случайности вследствие инициализации моделей случайными весами. Примерно после 250–300 итераций обновлений матрицы весов графики переплетаются в единый пучок и идут дальше вместе.
Увеличение масштаба графика позволяет выявить основную тенденцию: с увеличением числа нейронов в слое увеличивается количество итераций для достижения локальных минимумов и в целом для обучения нейронной сети. При этом локальные минимумы нейронных сетей с большим количеством нейронов опускаются ниже, и их графики обладают меньшей частотой колебаний.
В целом же на протяжении всего обучения модель с 60 нейронами демонстрирует наилучшие показатели. С небольшим отставанием почти параллельно идет график модели с 40 нейронами в скрытом слое. Для модели же с 80 нейронами в скрытом слое 1000 итераций обновления матрицы весов оказалось недостаточно. Эта модель демонстрирует более медленное снижение значения функции потерь. В то же время график динамики значений функции потерь демонстрирует потенциал снижения значения функции потерь при дальнейшем обучении модели. И есть все основания ожидать снижение показателей, достигнутых моделью с 60 нейронами в скрытом слое.
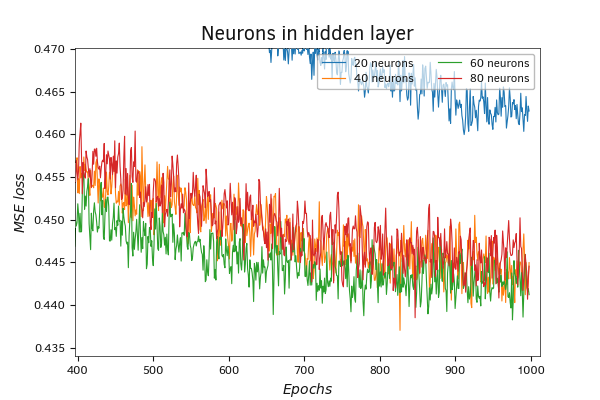
Сравнение динамики функции потерь при использовании разного количества нейронов в скрытом слое (масштаб)
Однако следует обратить внимание на то, что снижение ошибки на обучающей выборки может быть связано и с переобучением модели. Поэтому перед практическим использованием обученной модели всегда следует провести ее тестирование на «незнакомых» данных.
Обучение, валидация, тестирование.
В процессе обучения мы подбираем такие параметры матрицы весов, чтобы добиться минимальной ошибки на обучающей выборке. Но как поведет себя модель на новых данных за пределами обучающей выборки? Следует еще учесть, что мы имеем дело с нестатичными данными, которые постоянно меняются, и на их изменение оказывает влияние большое количество факторов. Некоторые из таких факторов нам известны, а о некоторых мы даже не догадываемся. И даже об известных нам факторах мы не можем с точностью сказать, как они изменятся в будущем. И тем более мы не знаем, как это повлияет на изменение изучаемых данных. Наиболее вероятным будет ухудшение показателей работы нейронной сети на новых данных. Но каким будет это ухудшение? Готовы ли мы нести такие риски?
Первым шагом на пути решения этого вопроса является валидация параметров обучения модели. Для валидации модели используется набор данных, не входящих в обучающую выборку. Чаще всего весь набор исходных данных делится на три блока:
- обучающая выборка (~60%),
- валидационная выборка (~20%),
- тестовая выборка (~20%).
Процентное соотношение для каждой выборки приведено условно и может сильно отличаться в зависимости от поставленной задачи.
Суть процесса валидации заключается в проверке параметров обучаемой модели на данных, не входящих в обучающую выборку. В процессе валидации подбираются гиперпараметры обучаемой модели для достижения максимального результата.
При написании скрипта полносвязного перцептрона на языке Python мы выделили 20% от обучающей выборки для валидации. Обучение первой модели продемонстрировало результаты схожие с полученными при обучении модели, созданной в MQL5. Это положительный для нас сигнал. Получение схожих результатов при обучении моделей созданных в трех разных языках программирования может свидетельствовать о правильности реализации выстроенного нами алгоритма.
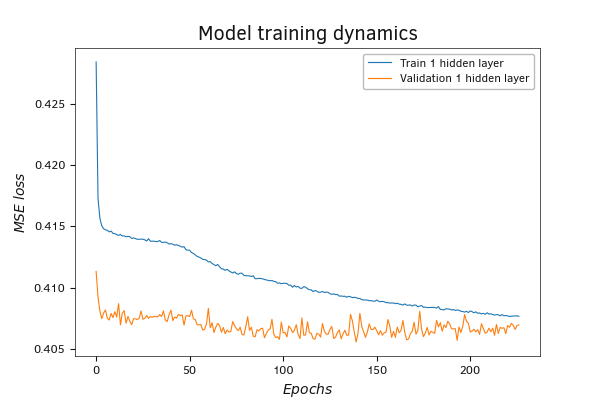
Изменение показателей модели с одним скрытым слоем на валидации в темпе с её обучением
Оценивая графики результатов тестирования, можно заметить тенденцию к снижению ошибки в процессе обучения. Это положительный фактор, который свидетельствует о способности модели к обучению и выстраиванию зависимостей между исходными данными и целевыми метками. В то же время можно заметить рост ошибки на валидационных данных, что может говорить как о переобучаемости модели, так и о нерепрезентативности данных валидационной выборки.
Дело в том, что мы указали долю данных для валидации в обучающей выборке. В этом случае библиотекой TenzorFlow берутся последние данные в наборе обучающей выборки. Но такой подход не всегда дает верный результат, ведь на результаты отдельно взятого периода могут большое влияние оказывать локальные тенденции.
В представленном ниже графике я вижу влияние обоих факторов. Общая динамика к росту ошибки на валидационных данных свидетельствует о склонности модели к переобучению, а начальное положение ошибки валидации ниже ошибки обучения может говорить о влиянии локальных тенденций.
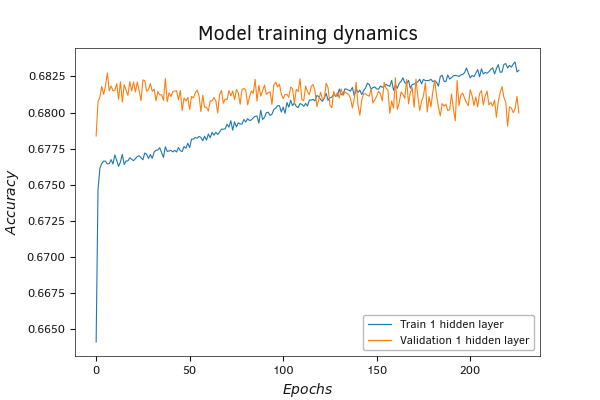
Изменение показателей модели с одним скрытым слоем на валидации в темпе с её обучением
График метрики accuracy демонстрирует схожие тенденции. Сам показатель отображает долю правильных ответов модели в общем объеме результатов. Здесь мы видим рост показателя в процессе обучения при практически неизменном показателе на валидации. Это может свидетельствовать о том, что модель учит паттерны, не встречающиеся в валидационной выборке.
Теоретически добавление скрытых слоев должно повысить способность модели к обучению и распознаванию более сложных паттернов и фигур. Вторую модель в Python мы создали с тремя скрытыми слоями. Действительно, в этой модели на обучении ошибка значительно снизилась. Но в то же время она еще больше возросла в процессе валидации. Это явный признак переобученности модели. Когда модель в силу своих возможностей не обобщает зависимости, а просто «заучивает» пары «исходные данные — целевые значения», на новых данных, не входящих в обучающую выборку, результат проявляется случайным образом.
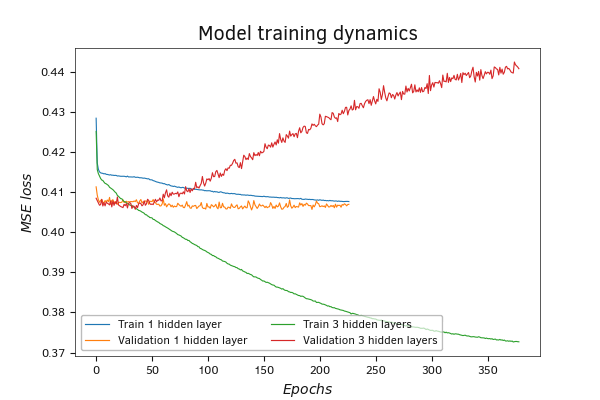
Изменение показателей модели с тремя скрытыми слоями на валидации в темпе с её обучением
Динамика метрики accuracy имеет тенденции схожие с функцией потерь. С той лишь разницей, что функция потерь снижается в процессе обучения, а accuracy растет.
Один из способов борьбы с переобучением является регуляризация модели. В третью модель мы добавили регуляризацию ElasticNet, и она сделала свое дело. При обучении модели с регуляризацией ошибка снижалась с меньшей скоростью. В то же время и на валидации рост ошибки замедлился.
И вновь на графике метрики accuracy мы наблюдаем те же тенденции, что и на графике функции потерь.
Надо сказать, что параметры ни обучения, ни регуляризации тщательно не подбирались. Поэтому, результаты обучения нельзя считать окончательными.
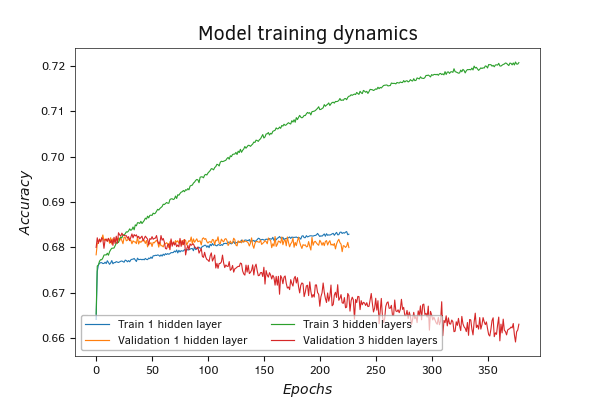
Изменение показателей модели с тремя скрытыми слоями на валидации в темпе с её обучением
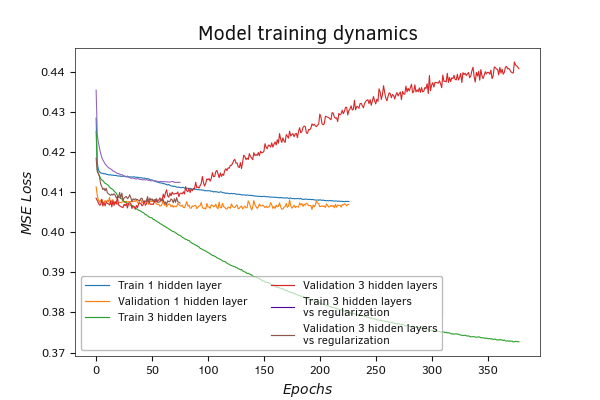
Изменение показателей модели с тремя скрытыми слоями и регуляризацией на валидации в темпе с её обучением
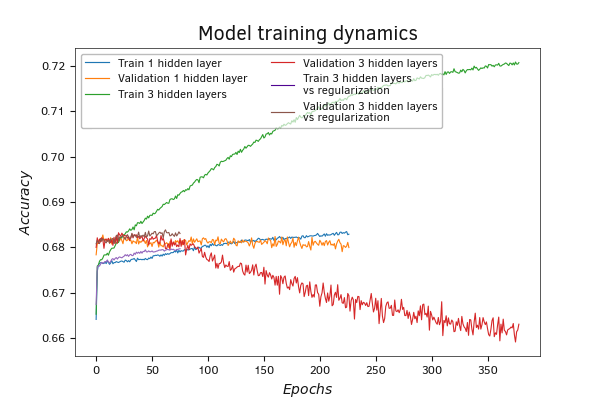
Изменение показателей модели с тремя скрытыми слоями и регуляризацией на валидации в темпе с её обучением
После обучения моделей проверим их на тестовой выборке. В отличие от валидации, минимальную ошибку на тестовой выборке показала именно модель с тремя скрытыми слоями без регуляризации. Модель с регуляризацией показала максимальную ошибку. Такое различие результатов между тестовой и валидационной выборками можно постараться объяснить способом создания выборок. Если в валидационную выборку попали только последние данные из обучающей выборки, то в тестовую выборку собирались случайные наборы данных из всей совокупности. Таким образом, тестовую выборку можно считать более репрезентативной, так как она лишена влияния локальных тенденций.
Измерение метрики accuracy на тестовой выборке показало аналогичные результаты. Наилучший результат показала модель с тремя скрытыми слоями.
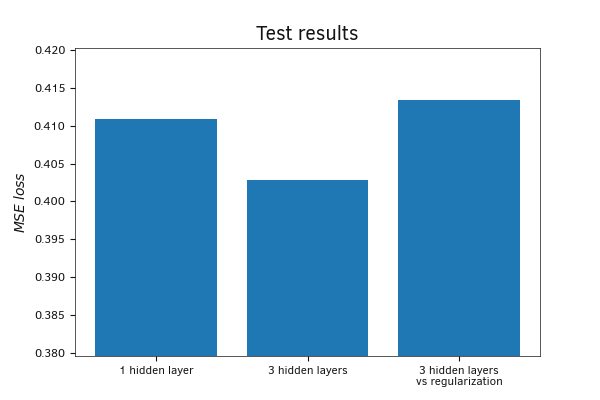
Сравнение результатов моделей на тестовой выборке
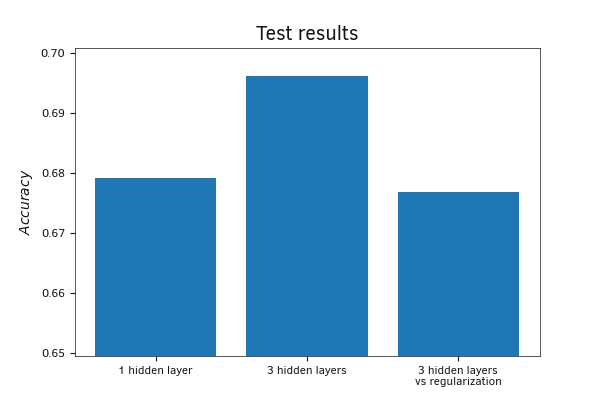
Сравнение результатов моделей на тестовой выборке
Можно подвести итоги нашей небольшой практической работы.
- Нормализация исходных данных перед подачей на вход нейронной сети сильно повышает шансы на сходимость нейронной сети и сокращает время на ее обучение.
- Коэффициент обучения должен тщательно подбираться экспериментальным путем. Слишком большой коэффициент обучения ведет к разбалансированию нейронной сети и росту ошибки. Слишком маленький коэффициент обучения ведет к увеличению времени и расходованию вычислительных ресурсов на обучение нейронной сети. При этом повышается риск остановки процесса обучения в локальном минимуме без достижения желаемого результата.
- Увеличение числа нейронов в скрытом слое дает улучшение результатов обучения. Но при этом растут и затраты на обучение. При выборе размера скрытого слоя необходимо найти баланс между ошибкой обучения и затратами ресурсов на проведение обучения нейронной сети. При этом следует помнить, что чрезмерное увеличение числа нейронов в скрытом слое повышает риск переобучения нейронной сети.
- Увеличение числа скрытых слоев также повышает способность модели к обучению и распознаванию более сложных фигур и конструкций. При этом сильно возрастает склонность модели к переобучению.
- Использование набора последних значений обучающей выборки для валидации не всегда способно показать истинные тенденции, так как такая валидационная выборка сильно подвержена влиянию локальных тенденций и не может быть репрезентативной.
Однако мы создаем модель для работы на финансовых рынках. Нам важно получение прибыли как в перспективе, так и в текущий момент. Конечно, какие-то локальные потери могут быть, но они не должны быть большими и частыми. Поэтому нам важно получить приемлемые результаты как на отдельном локальном участке данных, так и на более репрезентативной выборке. И наверное, получение лучших результатов на локальном участке имеет больший вес — после получения локальной прибыли мы можем переобучить модель для адаптации к новым тенденциям и получения прибыли на новом локальном участке. В то же время, если затраты на обучения будут превышать возможные локальные убытки, то больший вес приобретает доходность на длинном временном периоде с использованием репрезентативной выборки.