Обсуждение статьи "Прогнозирование временных рядов при помощи экспоненциального сглаживания"
Продраться через дебри кода не удается, но хотелось бы сравнить.
Исходная котировка
Имеем следующие варианты сглаживания:
Результат сглаживания
Уравнение регрессии:
eurusd =с(1)*eurusdsm(-1) + с(2)*trend + c(3)
Оценка уравнения регрессии
| Переменная | Коэф | Станд.ош. | t-статись | Вероятность |
| EURUSDSM(-1) | 0.759607 | 0.049127 | 15.46225 | 0.0000 |
| REND | 0.000207 | 5.79E-05 | 3.577804 | 0.0005 |
| C | 0.314884 | 0.065276 | 4.823886 | 0.0000 |
R-квадрат = 0.788273
Стандартная ошибка регрессии = 0.015172
Из полученных цифр отмечаем:
все коэффициенты регрессии знАчимы (вероятность их равенста нулю, равна нулю)
достаточно высокий (но не очень) R-квадрат, который говорит, что 78% дисперсии регрессия объясняет
стандартная ошибка равна 151 пипсов. Огромная цифра.
Можно ли доверять полученным цифрам?
Я бы не стал, так как по Жарку-Беру вероятность того, что сглаженный ряд имеет нормальное распределение, равна 31%.
Построим прогноз:
Ошибка прогноза не далеко ушла от ошибки регрессии и превосходит 100 пипсов
Давайте посмотрим на график ошибки прогноза:
Ну это полный финиш: ошибка переменная, а это означает неизвестность поведения прогноза будущем!
Для выяснения причины посмотрим на коррелированность коэффициентов уравнения регрессии:
Можно считать, что коэффициенты с(1) и с(3) практически на 100% коррелированы.
Мой вывод: использовать экспоненциальное сглаживание для прогноза нельзя.
Почему у нас разные результаты?
Для меня очевидно, что найденные Вами оптимальные параметры, не более, чем банальная подгонка. Сама регрессия безнадежна, коэффициенты в ней коррелированы.
Для меня очевидно, что найденные Вами оптимальные параметры, не более, чем банальная подгонка. Сама регрессия безнадежна, коэффициенты в ней коррелированы.
Спасибо за проявленный к статье интерес.
Пожалуйста, уточните, что Вы имели в виду? Какие результаты не сходятся и какие оптимальные параметры?
Пожалуйста, уточните, что Вы имели в виду?
Пардон, вы говорите, что можно использовать, а у меня вывод что нельзя.
Что использовать и для чего?
В завершении следует отметить, что модели экспоненциального сглаживания в определенных случаях в состоянии давать прогнозы, не уступающие по точности прогнозам, полученным при использовании более сложных моделей, при этом лишний раз подтверждая тот факт, что самая сложная модель далеко не всегда является самой лучшей.
Мой вывод: использовать экспоненциальное сглаживание для прогноза нельзя.
О чем ваши вопросы и зачем они?
Мой вывод: использовать экспоненциальное сглаживание для прогноза нельзя.
О чем ваши вопросы и зачем они?
Я бы с удовольствием попытался на что ни будь ответить, но мне для этого как минимум надо знать вопрос. Иначе мне придется гадать и фантазировать.
Попробую еще раз уточнить.
Модели экспоненциального сглаживания не могут быть использованы для прогноза пары еурюсд, любых котировок или вообще никогда?
P.S.
У Вас в тексте: “Уравнение регрессии: eurusd =с(1)*eurusdsm(-1) + с(2)*trend + c(3)”. Зачем регрессия, статья про модели экспоненциального сглаживания, а там другая модель, там вместо c(3) случайная величина с каким-то распределением и дисперсией?
У Вас в тексте: “Уравнение регрессии: eurusd =с(1)*eurusdsm(-1) + с(2)*trend + c(3)”. Зачем регрессия, статья про модели экспоненциального сглаживания, а там другая модель, там вместо c(3) случайная величина с каким-то распределением и дисперсией?
Не получается, разговор слепого с глухим. Отложим.
Еще раз поздравляю с хорошей статьей.
Не получается, разговор слепого с глухим. Отложим.
Еще раз поздравляю с хорошей статьей.
На самом деле мне очень любопытна Ваша точка зрения на прогнозирование с использованием экспоненциального сглаживания. Многих вещей я просто не знаю и всегда с радостью при каждой возможности пытаюсь открыть для себя чего то новое поэтому и задаю вопросы.
Если сильно не затруднит, пожалуйста, поясните, почему если распределение исходной последовательности (или сглаженной исходной последовательности) не нормальное, то доверять прогнозу нельзя? Или я не правильно Вас понял?
Спасибо за поздравление.
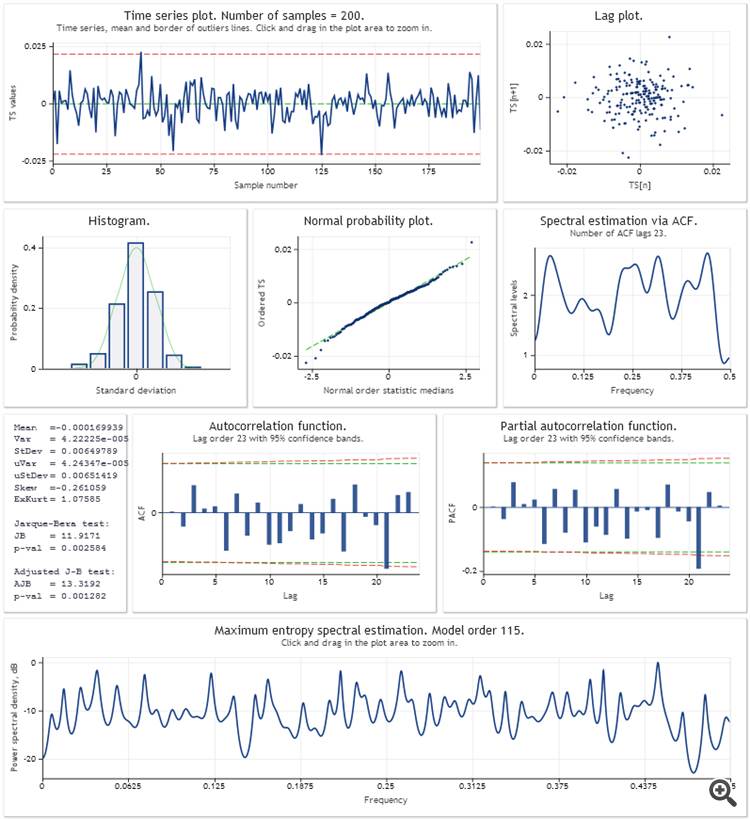
Вот анализ ошибок предсказания на один шаг вперед для аддитивной модели линейного роста с демпфированием. Параметры модели оптимизировались по выборке из последних 200 значений USDJPY,M1. Таким же способом как и в скрипте Optimization_Test.mq5 из статьи.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Опубликована статья Прогнозирование временных рядов при помощи экспоненциального сглаживания:
Автор: Victor