Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Боже мой. Не мог подумать, что так произойдёт)))
Боже мой. Не мог подумать, что так произойдёт)))
Нет. я не верю этим индикаторам.
Они врут.
Не верьте индикаторам. Верьте МНЕ.
Нет. я не верю этим индикаторам.
Они врут.
Не верьте индикаторам. Верьте МНЕ.
Мюллер говорил немножко не так: верить нельзя никому... , мне можно.)
Мюллер говорил немножко не так: верить нельзя никому... , мне можно.)
Вы удосужились рассмешить меня сегодня в одиннадцатый раз))). Десять раз когда читал соседнюю ветку.
Но мне точно можно верить. Я ж не Мюллер))
Это результат определения разницы между экстремумами в зависимости от изменения порогового значения для ЗЗ Каги. Рисунок б) -кумулятивная кривая.
То же самое для ЗЗ Ренко.
Заметила интересную особенность: Распределение Хи-квадрат:
Смотрите, при k=1, просматривается подобие ЗЗ Каги, при k=2, экспонента, абсолютно так же как на графике ЗЗ Ренко.
Распределение Хи-квадрат с увеличением k стремится к нормальному.
Ну, не знаю...
Особенность интересная, но как ей воспользоваться? Трудно что-либо предложить, учитывая, что я не шарю ни в Каги, ни в Ренко от слова "совсем".
Но, я попробую.
1. Надо отказаться от желания достичь нормального распределения и столетиями искать его. Работать с уже найденными закономерностями - это уже очень-очень много.
2. https://en.wikipedia.org/wiki/Generalized_normal_distribution
3. Проще говоря, кси-квадрат с к=1 это сумма квадратов нормально распределенных СЧ, кси-квадрат с к=2 - сумма СЧ с распределением Лапласа
4. Меня заинтересовал случай с к=2, т.к. исследования показывают, что на рынке господствует распределение Лапласа (точнее - двойное геометрическое)
5. Вот тут непонятно - в этих Ренко чё считается-то?? Сумма разностей (High-Low)?
6. Если так - то разность (High-Low) в Ренко есть СВ принадлежащая распределению Лапласа - это надо еще подтвердить экспериментально.
7. Тогда сумма разностей (High-Low) в скользящем окне (для определенного объема выборки) образует кси-квадрат с к=2 с известной квантильной функцией
https://keisan.casio.com/exec/system/1180573197
8. Ждем выхода (High-Low) в скользящем окне за границы доверительного интервала для определенного квантиля и входим в сделку.
Ну, это так - черновой набросок алгоритма, просто, чтобы развить тему и не более того :)))
5. Вот тут непонятно - в этих Ренко чё считается-то?? Сумма разностей (High-Low)?
7. Тогда сумма разностей (High-Low) в скользящем окне (для определенного объема выборки) образует кси-квадрат с к=2 с известной квантильной функцией
https://keisan.casio.com/exec/system/1180573197
8. Ждем выхода (High-Low) в скользящем окне за границы доверительного интервала для определенного квантиля и входим в сделку.
5. Ренко считает пробой диапазона заданного "кирпичиком Ренко" на величину 1 "кирпичика", причем пробой должен быть на величину "кирпичика", т.е. "кирпичик" 10 пп, чтобы нарисовать новый кирпичик Ренко нужно чтобы цена прошла выше уже сформированного бара Ренко 10 пп+1пп (или ниже на 10пп+1 пп) и тогда нарисуем новый "кирпичик". Т.е. по сути дискретизируется цена без учета времени на величину "кирпичика Ренко". Ренко убирает шумовые составляющие цены, но как и в любом фильтре появляется запаздывание, чтобы нарисовать новый бар Ренко цена должна пройти 2 диапазона = 2 высоты кирпичика Ренко
7,8 это индикатор ATR, то что Вы пишете обычно называют пробоем волатильности, но и тут извечная проблема - период ATR, если период маленький, то будут шумы, если период большой то будет запаздывание
Здесь
Форум по трейдингу, автоматическим торговым системам и тестированию торговых стратегий
ЗигЗаги Пастухов
Novaja, 2018.08.26 23:22
Это результат определения разницы между экстремумами в зависимости от изменения порогового значения для ЗЗ Каги. Рисунок б) -кумулятивная кривая.
То же самое для ЗЗ Ренко.
Заметила интересную особенность: Распределение Хи-квадрат:
Смотрите, при k=1, просматривается подобие ЗЗ Каги, при k=2, экспонента, абсолютно так же как на графике ЗЗ Ренко.
Распределение Хи-квадрат с увеличением k стремится к нормальному.
Novaja говорит о какой-то разнице между экстремумами... О размахе (High-Low) что ли? Понять не могу... Слишком сухо и сжато написано...
Но, на кси-квадрат похоже - поэтому я и заинтересовался. Найти явные закономерности - большая редкость.
Ну, не знаю...
Особенность интересная, но как ей воспользоваться? Трудно что-либо предложить, учитывая, что я не шарю ни в Каги, ни в Ренко от слова "совсем".
Но, я попробую.
1. Надо отказаться от желания достичь нормального распределения и столетиями искать его. Работать с уже найденными закономерностями - это уже очень-очень много.
2. https://en.wikipedia.org/wiki/Generalized_normal_distribution
3. Проще говоря, кси-квадрат с к=1 это сумма квадратов нормально распределенных СЧ, кси-квадрат с к=2 - сумма СЧ с распределением Лапласа
4. Меня заинтересовал случай с к=2, т.к. исследования показывают, что на рынке господствует распределение Лапласа (точнее - двойное геометрическое)
5. Вот тут непонятно - в этих Ренко чё считается-то?? Сумма разностей (High-Low)?
6. Если так - то разность (High-Low) в Ренко есть СВ принадлежащая распределению Лапласа - это надо еще подтвердить экспериментально.
7. Тогда сумма разностей (High-Low) в скользящем окне (для определенного объема выборки) образует кси-квадрат с к=2 с известной квантильной функцией
https://keisan.casio.com/exec/system/1180573197
8. Ждем выхода (High-Low) в скользящем окне за границы доверительного интервала для определенного квантиля и входим в сделку.
Ну, это так - черновой набросок алгоритма, просто, чтобы развить тему и не более того :)Cgfcb,j
Спасибо большое, замечательный комментарий.
Несколько слов по построению зз. Вариант Каги.
Синим цветом показан тиковый график, порог-3п. Если противоход больше 3п. рисуется экстремум, если нет, идем дальше. Т.е. свинги могут содержать 2,66; 3,66; n-ное число таких порогов(отрезков) причем дробное значение. В построении типа Ренко это дробное значение отбрасывается, а принцип тот же. Т.е. целые значание 2,3, и т.д. Т.е. видим как дробные вершинки не учитываются в построении. На рисунке ниже вариант Ренко.
Теперь думаю отличие понятно. Так вот, частота появления отношения длины свинга к пороговому значению(отрезку в 3п.) для Каги: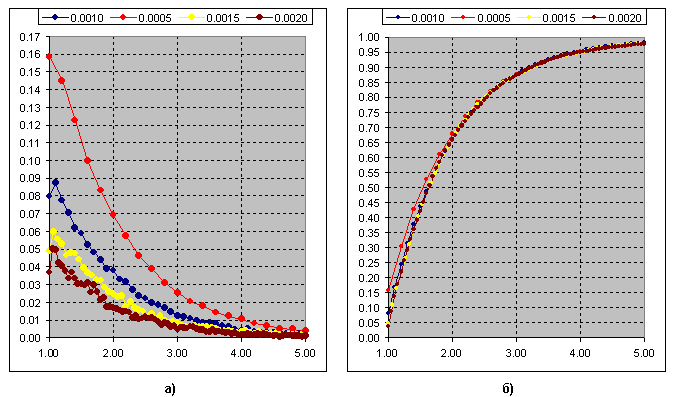
Рис.б) Кумулятивная сумма кривых. Распределение Хи-квадрат при k=1 подходит под эту кривую.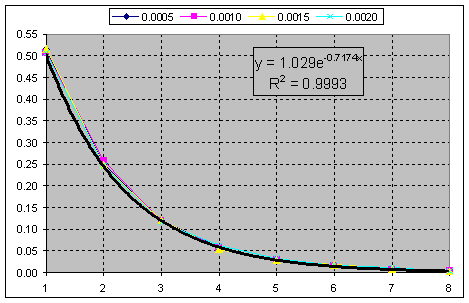
А это кумулятивная сумма частоты появления отношения свинга к порогу(отрезку) для построения Ренко. Хи-квадрат при k=2.
Т.е. стоит только отбросить дробные части как получаем чистую экспоненту.
Спасибо большое, замечательный комментарий.
Несколько слов по построению зз. Вариант Каги.
Синим цветом показан тиковый график, порог-3п. Если противоход больше 3п. рисуется экстремум, если нет, идем дальше. Т.е. свинги могут содержать 2,66; 3,66; n-ное число таких порогов(отрезков) причем дробное значение. В построении типа Ренко это дробное значение отбрасывается, а принцип тот же. Т.е. целые значание 2,3, и т.д. Т.е. видим как дробные вершинки не учитываются в построении. На рисунке ниже вариант Ренко.
Теперь думаю отличие понятно. Так вот, частота появления отношения длины свинга к пороговому значению(отрезку в 3п.) для Каги:
Рис.б) Кумулятивная сумма кривых. Распределение Хи-квадрат при k=1 подходит под эту кривую.
А это кумулятивная сумма частоты появления отношения свинга к порогу(отрезку) для построения Ренко. Хи-квадрат при k=2.
Т.е. стоит только отбросить дробные части как получаем чистую экспоненту.
Свинги... Эх-ма... :)))
Ладно. Не буду глубоко вникать в терминологию. Некогда.
Имеем чистейшую экспоненту на чем-либо.
Сумма этих компонентов будет представлять из себя отрицательное биномиальное распределение (распределение Эрланга для непрерывных СВ) опять-таки, подчеркну, с известной дисперсией. В пределе - нормальное распределение, которое Вы ищете.