Разностное исчисление, примеры. - страница 6

Новый комментарий
 

Усреднение полиномом четвертой степени с плечом 72 (EMA четвертой степени) и экстраполяция на разное плечо при помощи кубической параболы (полинома третьей степени).

      a1_Buffer[i]=((open[i] - Znach)    +5061600*a1_Buffer[i+1 ]-7489800    *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975;

      a5_Buffer[i+92]=a1_Buffer[i];   if(i<=1100) { for(z=92-1;z>=0;z--){        a5_Buffer[i+0+z]=  4*a5_Buffer[i+1+z]  -  6*a5_Buffer[i+2+z]  +  4*a5_Buffer[i+3+z]  - 1*a5_Buffer[i+4+z];  }}


      a2_Buffer[i+20]=a5_Buffer[i+20]; 
      
      a3_Buffer[i+38]=a5_Buffer[i+38]; 
      
      a4_Buffer[i+56]=a5_Buffer[i+56];
        
      a6_Buffer[i+74]=a5_Buffer[i+74];

Первый рисунок - схема построения, на втором рисунке все не перерисовывающиеся линии выведены к последнему значению.

Индикаторы в подвале отличаются только заданным смещением линий.


 

Усреднение полиномом четвертой степени с плечом 72 (EMA четвертой степени) и экстраполяция на разное плечо при помощи полинома четвертой степени.

      a1_Buffer[i]=((open[i] - Znach)    +5061600*a1_Buffer[i+1 ]-7489800    *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975;

      a5_Buffer[i+92]=a1_Buffer[i];   if(i<=1100) { for(z=92-1;z>=0;z--){        a5_Buffer[i+0+z]=  5*a5_Buffer[i+1+z]  -  10*a5_Buffer[i+2+z]  +  10*a5_Buffer[i+3+z]  - 5*a5_Buffer[i+4+z]  +  1*a5_Buffer[i+5+z];  }}


      a2_Buffer[i+20]=a5_Buffer[i+20]; 
      
      a3_Buffer[i+38]=a5_Buffer[i+38]; 
      
      a4_Buffer[i+56]=a5_Buffer[i+56];
        
      a6_Buffer[i+74]=a5_Buffer[i+74];
  

Первый рисунок - схема построения, на втором рисунке все не перерисовывающиеся линии выведены к последнему значению.

Индикаторы в подвале отличаются только заданным смещением линий.


 

Алексей, могу Вам дать бесплатный совет и наводку. 

Я уже говорил, что применять сдвижку влево - это , как бы мягче сказать... - неблагодарное занятие. Получите только проклятья от тех, кто смотрит вашу ветку. Кстати,  это одна из причин, почему Вы в собственной ветке оказались в гордом одиночестве.
Но сдвигать влево периодическую линию с одной точкой перегиба на одну полуволну (точнее если существует только одна точка перегиба между локальным минимумом и максимумом) без фактической сдвижки можно с помощью производной этой функции. Это правда не фактическая сдвижка, а по сути. Производная от функции - это угол касательной к линии. Вычисляется просто: buf[i]-buf[i+1]

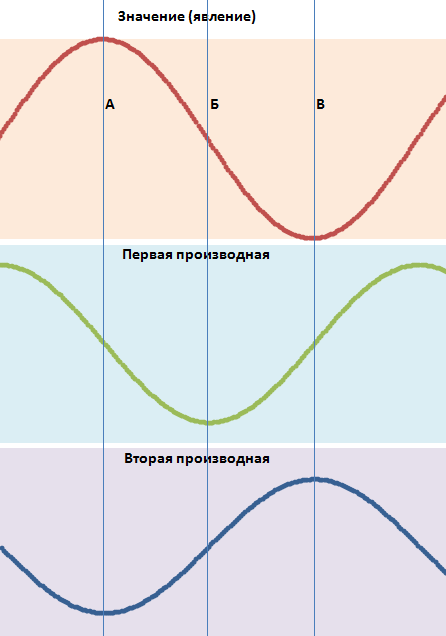
Вот например первая и вторая производные синусоиды. Точки перегиба самой функции становятся локальными максимумами и минимумами ее производной.

 
Nikolai Semko:

Алексей, могу Вам дать бесплатный совет и наводку. 

Я уже говорил, что применять сдвижку влево - это , как бы мягче сказать... - неблагодарное занятие. Получите только проклятья от тех, кто смотрит вашу ветку. Кстати,  это одна из причин, почему Вы в собственной ветке оказались в гордом одиночестве.
Но сдвигать влево периодическую линию с одной точкой перегиба на одну полуволну (точнее если существует только одна точка перегиба между локальным минимумом и максимумом) без фактической сдвижки можно с помощью производной этой функции. Это правда не фактическая сдвижка, а по сути. Производная от функции - это угол касательной к линии. Вычисляется просто: buf[i]-buf[i+1]

Вот например первая и вторая производные синусоиды. Точки перегиба самой функции становятся локальными максимумами и минимумами ее производной.

Да Николай, полностью с Вами согласен, и конечно каждая производная сдвигает график синусоиды на четверть периода влево. 

Поэтому когда речь зашла о сравнениях я устранил искусственную сдвижку линий. Это видно на вторых рисунках в последних постах. Все линии кроме тонкой серой, нарисованы на последнем баре и не перерисовываются. А некоторое смещение графика в лево происходит за счет экстраполяции.

А линии эти действительно еще можно продифференцировать, в нашем случае снять первую  и/или вторую разность.  Что и было в прототипе.  :)))

Сдвиг влево был использован, чтобы связать все линии включая линии построения в цельную картину, и увидеть общую схему.

 
Aleksey Panfilov:

Да Николай, полностью с Вами согласен, конечно каждая производная сдвигает график синусоиды на четверть периода влево. 

Именно поэтому когда речь зашла о сравнениях я устранил искусственную сдвижку линий. Это видно на вторых рисунках в последних постах. Все линии кроме тонкой серой, нарисованы на последнем баре и не перерисовываются. А некоторое смещение графика в лево происходит за счет экстраполяции. 

Сдвиг влево был использован, чтобы связать все линии включая линии построения в цельную картину, и продемонстрировать общую схему.


На верхний график внимания можно даже не обращать, т.к. он сдвинут влево, а хвост перерисовывается. А нижний выглядит запаздывающим и буднично уныло. В чем смысл тогда всей этой суеты?

 
Nikolai Semko:

На верхний график внимания можно даже не обращать, т.к. он сдвинут влево, а хвост перерисовывается. А нижний выглядит запаздывающим и буднично уныло. В чем смысл тогда всех этой суеты?


))))

Посмотрим "по ходу пьесы". 

Пока все по плану. ))

 
Nikolai Semko:

Алексей, могу Вам дать бесплатный совет и наводку. 

Я уже говорил, что применять сдвижку влево - это , как бы мягче сказать... - неблагодарное занятие. Получите только проклятья от тех, кто смотрит вашу ветку. Кстати,  это одна из причин, почему Вы в собственной ветке оказались в гордом одиночестве.
Но сдвигать влево периодическую линию с одной точкой перегиба на одну полуволну (точнее если существует только одна точка перегиба между локальным минимумом и максимумом) без фактической сдвижки можно с помощью производной этой функции. Это правда не фактическая сдвижка, а по сути. Производная от функции - это угол касательной к линии. Вычисляется просто: buf[i]-buf[i+1]

Вот например первая и вторая производные синусоиды. Точки перегиба самой функции становятся локальными максимумами и минимумами ее производной.


Вот одна из возможных реализаций такого подхода. Никакого перерисовывания и сдвигов. Это вторая производная от Вашей линии.


Файлы:
Banzai.mq4  5 kb
Banzai.mq5  6 kb
 

Иногда даже очень коррелирует и не запаздывает


 
Nikolai Semko:

Алексей, могу Вам дать бесплатный совет и наводку. 

Я уже говорил, что применять сдвижку влево - это , как бы мягче сказать... - неблагодарное занятие. Получите только проклятья от тех, кто смотрит вашу ветку. Кстати,  это одна из причин, почему Вы в собственной ветке оказались в гордом одиночестве.
Но сдвигать влево периодическую линию с одной точкой перегиба на одну полуволну (точнее если существует только одна точка перегиба между локальным минимумом и максимумом) без фактической сдвижки можно с помощью производной этой функции. Это правда не фактическая сдвижка, а по сути. Производная от функции - это угол касательной к линии. Вычисляется просто: buf[i]-buf[i+1]

Вот например первая и вторая производные синусоиды. Точки перегиба самой функции становятся локальными максимумами и минимумами ее производной.

Что-то я сегодня в благодушном настроении

Алг. на "сдвижке машек влево" (фига себе названьице получилось :) )

1. Берём по классике два SMA - быструю и медленную.

2. Сдивгаем влево на полпериода каждую (каждую на свой).

3. С удивлением видим что :

    3.0 машки вьются вокруг друг-друга

    3.1. быстрая перемекает медленную вверх ровно перед экстремумом (подчас значительно ДО)

    3.2. пересечения "парные" (до экстремума вверх, после вниз)

4. Сдвигаем машки обратно в реальное время, но (в отличии от п2) на одинаковую величину. Одна будет заканчиваться в 0, другая выходить сильно вправо

5. Теперь увидив пересечение сих. машек смотрим где там прошедший экстремум и предыдущее пересечение. На основе чего можем отсеивать явные ложняки и делать весьма симпатичные входы.

 
Maxim Kuznetsov:

Что-то я сегодня в благодушном настроении

Алг. на "сдвижке машек влево" (фига себе названьице получилось :) )

1. Берём по классике два SMA - быструю и медленную.

2. Сдивгаем влево на полпериода каждую (каждую на свой).

3. С удивлением видим что :

    3.0 машки вьются вокруг друг-друга

    3.1. быстрая перемекает медленную вверх ровно перед экстремумом (подчас значительно ДО)

    3.2. пересечения "парные" (до экстремума вверх, после вниз)

4. Сдвигаем машки обратно в реальное время, но (в отличии от п2) на одинаковую величину. Одна будет заканчиваться в 0, другая выходить сильно вправо

5. Теперь увидив пересечение сих. машек смотрим где там прошедший экстремум и предыдущее пересечение. На основе чего можем отсеивать явные ложняки и делать весьма симпатичные входы.


Может быть в этом что-то и есть. Но это алгоритм не на сдвижке влево, а на сдвижке вправо. 


12345678910111213...24
Новый комментарий