О запаздывании скользящих средних

[Vladimir]

Говорят, что значения EMA "ближе" к последним курсам, чем SMA. Задумался, стал считать. В формулах ниже целое число n одинаковое, q=(n-1)/n - знаменатель геометрической прогрессии:

SMA=(X1+X2+...+Xn)/n; веса точек одинаковы и равны 1/n.

EMAслед=EMAпред + (Xслед - EMAпред)/n = Xслед/n + EMAпред*(n-1)/n = (1/n) (X1+X2*q+X3*q^2+X4*q^3+...); веса точек с каждым шагом уменьшаются 1/n  q/n  q^2/n  q^3/n ...

Запаздывание, или центр масс весов (при линейном росте X - точка, где значение Xi равно значению скользящей средней), для SMA где-то посередине учитываемых точек, около n/2. Покувыркавшись с вычислением суммы бесконечного ряда слагаемых вида i*q^i, нашел, что для EMA запаздывание равно n. В два раза больше, чем у SMA.

Если кто занимался вопросом, подскажите, так ли это? Или я где-то ошибся...

[Dmitry Fedoseev]

Горе от ума. Просто прикрепите на график SMA и EMA с одинаковым периодом и посмотрите. 

[Alexey Volchanskiy]

Vladimir:

Говорят, что значения EMA "ближе" к последним курсам, чем SMA. Задумался, стал считать. В формулах ниже целое число n одинаковое, q=(n-1)/n - знаменатель геометрической прогрессии:

SMA=(X1+X2+...+Xn)/n; веса точек одинаковы и равны 1/n.

EMAслед=EMAпред + (Xслед - EMAпред)/n = Xслед/n + EMAпред*(n-1)/n = (1/n) (X1+X2*q+X3*q^2+X4*q^3+...); веса точек с каждым шагом уменьшаются 1/n  q/n  q^2/n  q^3/n ...

Запаздывание, или центр масс весов (при линейном росте X - точка, где значение Xi равно значению скользящей средней), для SMA где-то посередине учитываемых точек, около n/2. Покувыркавшись с вычислением суммы бесконечного ряда слагаемых вида i*q^i, нашел, что для EMA запаздывание равно n. В два раза больше, чем у SMA.

Если кто занимался вопросом, подскажите, так ли это? Или я где-то ошибся...

SMA - обычный КИХ фильтр, можно посмотреть в сырцы, правда, они очень веселые )) \MQL5\Include\MovingAverages.mqh

Для SMA приводится фильтрация блока данных с линейными коэффициентами, простое усреднение

double SimpleMA(const int position,const int period,const double &price[])
  {
//---
   double result=0.0;
//--- check position
   if(position>=period-1 && period>0)
     {
      //--- calculate value
      for(int i=0;i<period;i++) result+=price[position-i];
      result/=period;
     }
//---
   return(result);
  

А для EMA почему-то только одного семпла

//+------------------------------------------------------------------+
//| Exponential Moving Average                                       |
//+------------------------------------------------------------------+
double ExponentialMA(const int position,const int period,const double prev_value,const double &price[])
  {
//---
   double result=0.0;
//--- calculate value
   if(period>0)
     {
      double pr=2.0/(period+1.0);
      result=price[position]*pr+prev_value*(1-pr);
     }
//---
   return(result);
  }

 ***

ключевое название переменной prev_value

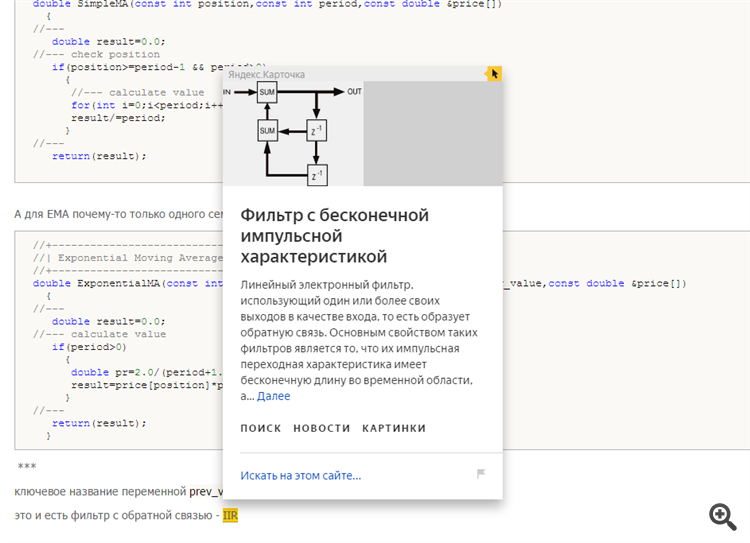
это и есть фильтр с обратной связью - IIR 

[Alexey Volchanskiy]

Alexey Volchanskiy:

Кстати, я пользуюсь Яндекс браузером, у него есть примочка, которая ищет то ли в Вики, то ли еще где... но находит вот такие начальные данные, надо щелкнуть по подчеркнутому слову. Рекомендую, удобно.

[Vladimir]

Dmitry Fedoseev:

Горе от ума. Просто прикрепите на график SMA и EMA с одинаковым периодом и посмотрите. 

Прикрепил. Скриншот прилагаю. Вывод обратен моему, показанный метатрейдером EMA на движениях опережает SMA, хоть и незначительно. Параметр "период" указан 14 обеим средним. Уже это вызывает подозрение, по справке параметром должен быть не период, а "доля использования значения цен". По совету Alexey Volchanskiy смотрю "сырцы" для MT4.

      double pr=2.0/(period+1.0);
      result=price[position]*pr+prev_value*(1-pr);

Там такой же, как в MT5, фокус с периодом, он принудительно делится на два внутри вычисляющей части. Это ополовинивание параметра нигде в справке не отражено, но, поскольку совпадает с моей оценкой, думаю, является подтверждением расчета центров масс. При одинаковых n у EMA он находится не в точке n/2, а в точке n. Слова о лучшем учете последних курсов оказались легендой. Веса-то у них действительно растут с приближением к последней точке, но в целом бесконечный хвост все же оттягивает центр масс назад, запаздывание растет.

[Igor Yeremenko]

Vladimir:

Если кто занимался вопросом, подскажите, так ли это? Или я где-то ошибся...

уже есть куча модификаций стандартной МА: AMA, Trix, JMA и тд выбирайте любой

тут подробнее https://www.mql5.com/ru/articles/1450

[Dmitry Fedoseev]

Vladimir:

... "доля использования значения цен"...

Так оно и есть. Период для EMA - это условное название ее параметра. 

[Vladimir]

Удивительно, столько ответов, и ни одного на заданный вопрос: "так ли это?". 

Вообще никого никогда не интересовало запаздывание скользящих средних, выходит...

[Dmitry Fedoseev]

Vladimir:

Удивительно, столько ответов, и ни одного на заданный вопрос: "так ли это?". 

...

Наверно здесь все рассчитывают на думающих собеседников, способных, хотя бы об очевидном, делать выводы самостоятельно

[Younga]

Vladimir:

Удивительно, столько ответов, и ни одного на заданный вопрос: "так ли это?". 

Вообще никого никогда не интересовало запаздывание скользящих средних, выходит...

А если они не запаздывают, а просто вы производите вычисления с заданной вами глубиной (периодом)?

[Vladimir]

Younga:
А если они не запаздывают, а просто вы производите вычисления с заданной вами глубиной (периодом)?

Как же не запаздывают. Я рассматривал самую грубую модель тренда, линейный рост курса X каждый шаг на величину dX, Xi=X0+i*dX. Посчитайте, простая скользящая средняя, учитывающая 11 точек (10 шагов), будет стабильно идти ниже курса на 5*dx, то есть постоянно отставать на 5 шагов. А экспоненциальная, по моим подсчетам, тоже пойдет ниже курса, но отставать будет на 10 точек. Поскольку мой вывод противоречит известным словам о том, что EMA лучше учитывает последние изменения, я и задал вопрос. Раньше меня это не интересовало, но сейчас потребовалось знать наверняка. Терминал меня удивил, под видом двух средних с n=14 он показал одну с n=14, другую с n=7. Ничем не помог.

Рекомендовали статью https://www.mql5.com/ru/articles/1450 "...алгоритмы усреднения с минимальным лагом...", прочитал, но сами лаги (запаздывания) в ней и не вычисляются, и не сравниваются. Опять ничего подходящего.

Придется, наверное, моделировать линейный тренд, SMA, EMA в электронных таблицах и проверять самому. Жаль. Так хотелось получить ссылку на источник, где центры масс весов скользящих средних разного вида давно подсчитаны и проверены. В одиночку и ошибиться недолго.