Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Если приращения случайны, то цена - это random walk, она имеет нормальное распределения, и заработать на ней гарантированно нельзя.
Однако надо оговорить природу приращения, сказать просто "случайная" - не сказать ничего. В жизни всё случайно. У автобуса есть расписание, но время его прибытия величина случайная. Случайные приращения цены могут быть коррелированы с фазами луны, например, это не делает их неслучайными.
Чтобы получить random walk приращения должны быть iid независимыми и одинаково распределёнными.
В том то и дело, что приращение цены не нормально распределено. Иначе заработать на нем было бы гарантированно можно.
В том то и дело, что приращение цены не нормально распределено. Иначе заработать на нем было бы гарантированно можно.
относительно чего ненормальны приращения?
В том то и дело, что приращение цены не нормально распределено. Иначе заработать на нем было бы гарантированно можно.
Приращение цены можно считать нормально распределённым - это достаточно близко к реальности, однако это ничего не даст, если оно iid . Можно считать приращение цены t-распределённым со степенью свободы 4 или 5. Это гораздо ближе к реальности, чем допущение о нормальности приращений.
Результирующий процесс будет random walk. Вот он-то вообще гарантированно нормально распределённый, независимо от распределения приращений, но от той нормальности никакого прока - нельзя заработать на случайном блуждании. Приращение цены можно считать стационарными, но их нельзя торговать. Торговать можно цену, а она random walk, процесс нестационарный. По крайней мере в контексте данного топика.
Приращение цены можно считать нормально распределённым - это достаточно близко к реальности, однако это ничего не даст, если оно iid . Можно считать приращение цены t-распределённым со степенью свободы 4 или 5. Это гораздо ближе к реальности, чем допущение о нормальности приращений.
Результирующий процесс будет random walk. Вот он-то вообще гарантированно нормально распределённый, независимо от распределения приращений, но от той нормальности никакого прока - нельзя заработать на случайном блуждании. Приращение цены можно считать стационарными, но их нельзя торговать. Торговать можно цену, а она random walk, процесс нестационарный. По крайней мере в контексте данного топика.
Можно я для поддержания дискуссии немножко поспорю? Я сейчас сам не очень уверен в том, что хочу сказать. Тем более уже очень поздно. Но все-таки... Если приращения какой-то величины нормально распределены, то это значит, что эта величина ограничена. (Ошибаюсь?)
Если не ошибся в предыдущем утверждении, то во множестве значений величины есть максимумальное и минимальное. Кроме того, чем ближе значение величины к максимальному или минимальному, тем больше вероятность его изменения в сторону среднего. Вот это и есть закон, который можно использовать.
п.с. Не подумайте, что я нападаю. Просто хочу поговорить с умным человеком.
Можно я для поддержания дискуссии немножко поспорю? Я сейчас сам не очень уверен в том, что хочу сказать. Тем более уже очень поздно. Но все-таки... Если приращения какой-то величины нормально распределены, то это значит, что эта величина ограничена. (Ошибаюсь?)
Если не ошибся в предыдущем утверждении, то во множестве значений величины есть максимумальное и минимальное. Кроме того, чем ближе значение величины к максимальному или минимальному, тем больше вероятность его изменения в сторону среднего. Вот это и есть закон, который можно использовать.
п.с. Не подумайте, что я нападаю. Просто хочу поговорить с умным человеком.
про теорему арксинуса и ошибку игрока - не слышали?
Я не зря спросил о относительности отклонения.
Если это returns - одна песня.
МА(x периода) - другой мотивчик...
Если вместо MA использовать TrueDMA - совсем иная какафония вас постигнет.
;)
Хде вам удалось ненормальность получить?
У кого не спрашиваю, молчат.
Есть тема - показано обратное.
Йо моё...
:)
Можно я для поддержания дискуссии немножко поспорю? Я сейчас сам не очень уверен в том, что хочу сказать. Тем более уже очень поздно. Но все-таки... Если приращения какой-то величины нормально распределены, то это значит, что эта величина ограничена. (Ошибаюсь?)
Если не ошибся в предыдущем утверждении, то во множестве значений величины есть максимумальное и минимальное. Кроме того, чем ближе значение величины к максимальному или минимальному, тем больше вероятность его изменения в сторону среднего. Вот это и есть закон, который можно использовать.
п.с. Не подумайте, что я нападаю. Просто хочу поговорить с умным человеком.
Однозначно ошибаешься. Характер распределения ничего не говорит об ограничении величины. Наверняка есть какие-нубудь исключения, но в общем случае так. Ограничения накладываются параметрами распределения. Например: нормально распределённые преращения ~N(0,1). Это стационарный процесс, он имеет ограничения величины, он практически никогда не достигнет 4 или -4.
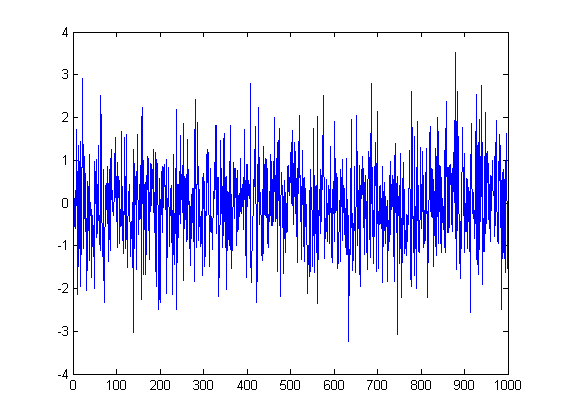
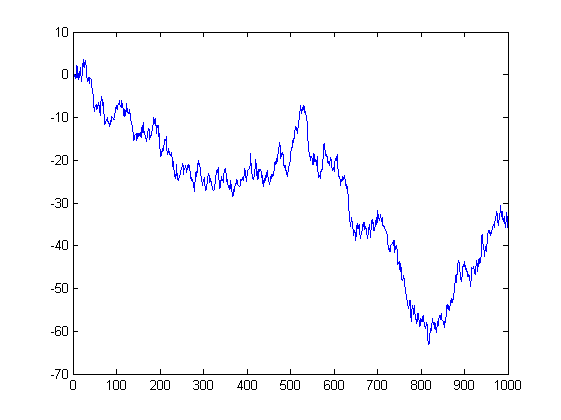

А вот цена, которая получилась из этих приращений. Это случайное блуждание. Оно тоже имеет нормальное распределение ~N(0,sigma^2), но его параметер дисперсии не константа, а растёт с увеличением времени, т.е. количества приращений. Естественно, никаких ограничений по величине этот процесс не имеет и с одинаковой вероятностью посетит все точки. На этом основана задача о раззорении игрока - если играть достаточно долго в абсолютно честную игру (50:50), то всё равно проиграешь, т.к. рано или поздно вот эта кривая заведёт тебя ниже, чем у тебя есть денег.
А вот 1000 случайных блужданий, очевидно виден колокол нормального распределения.
А вот то, что ты говоришь о возврате к среднему, это совсем другая история, это mean-reverting процесс - autoregressive (AR)
x(i) = a * x(i-1) + e(i). e(i) преращения ~N(0,1), a < 1.
Если ты нашёл торгуемый mean-reverting процесс, то тут только успевай корзинки с капустой оттаскивать. Естественно, зависит от параметров - скорости возврата к среднему (a) - но в любом случае всё круто.
А вот 1000 случайных блужданий, очевидно виден колокол нормального распределения.
нужно частотами попадания осветить.
--
расширяющийся двойной Царь(log) Колокол.
;)
не всякий увидит.
На тебе гистограмму и пробабилити плот для 1000-го отсчёта.


Хотя исходя из того, что приращения были нормальные, сумма нормальных распределений есть нормальное распределение. Тут ничего даже и проверять-то не надо.
На тебе гистограмму и пробабилити плот для 1000-го отсчёта.
Хотя исходя из того, что приращения были нормальные, сумма нормальных распределений есть нормальное распределение. Тут ничего даже и проверять-то не надо.
Сенкс!
Хорошая (вернее -еще и наглядно полезная;) работа.