Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Вот я и думаю, что постановка задачи в самом начале является узкой, в самом узком смысле этого слова. Сдается мне, что это никакого отношения к общему случаю не имеет. :о( Но возможно - ошибаюсь.
Ну тык, батенька! Я тут с узким-то кувыркаюсь - с трудом вместе свё связываю, а ты мне пошире наровишь рамки раздвинуть:-)
Вот и давай, выбирай себе самую широкую постановку и покажи как нужно. Мы поучимся. А пока, чё могём, то и творём.
Продолжим рассмотрение перехода от идеальной ТС, ФР распределения взяток которой дельтообразно и сидит в оптимуме на двойном спреде (рис. слева, красненьким) к оптимальной: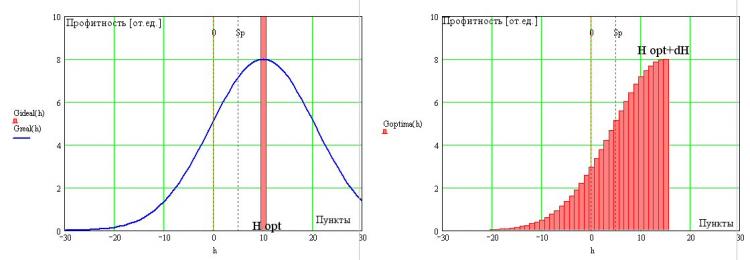
Мы, конечно, должны признать, что в реальности, без возможности заглядывать в будущее (находясь на правом краю ВР), мы вынуждены мириться ошибками работы оптимальной ТС которые неизбежны в силу отсутствия в Природе чудес (это уже было оговорено специально). Следовательно, ФР оптимальной ТС будет иметь размывание дельтафункционального распределения своего идеального прототипа так, как это показано на том же рис. синей линеей.
Из-за того, что все открываемые позиции автоматически начинаются с отрицательной величины в -Sp, даже для оптимальной ТС мы точно будем иметь транзакции с отрицательным исходом. Причём, сами сделки могут быть закрыты со сколь угодно большим минусом (работу с защитными ордерами мы пока опустим). Это неизбежное условие реальности. Но для правого края мы можем менять форму и у нас есть некая степень свободы. Связано это очевидно с тем, что мы вправе сами выбирать, когда закрывать профитную селку. Помня о том, что существует некий оптимум для величины профита Н, мы вправе предположить наличие резкой границы справа у ФР взяток оптимальной ТС. Это требование связано, как я уже отмечал, с наличием двух конкурирующих процессов влияющих на профитность ТС - частоты совершения транзакций и их амплитуды. Итак, граница справа будет иметь место обязательно, но будет ли она совпадать с Н opt, как для идеальной ТС. Очевидно нет. И связано это с наличием неизбежного затянутого хвоста слева. В самом общем случае, правая граница ФР быдет лежать в области за Н opt (см. рис. справа) и её точное местонахождение пока на данном этапе рассуждений нам не важно.
Итак, получен общий вид модельного распределения взяток оптимальной ТС. Он обязательно будет иметь крутую правую границу, точное расположение которой определяется спредом Sp и монотонно убывающее правое крыло с обязательным заходом в отрицательную область. Точный вид этого крыла мы восстановим позже. Но можно уже сейчас сказать, что пологость (или крутость) левого склона определяется отсутствием или наличием (их силой) закономерностей в исходном ценовом ряде, а интеграл от этой горы должен (согласно т. Дуба) давать точный ноль на мартингале, что позже позволит нам найти её (ТС) некоторвые характеристики.
ystr писал(а) >> Если же принимать во внимание что "для идеальной ТС все направления угадываются" то должен заметить, что такая система на практике сложно реализуема. А если поставить условие, что "диапазон изменений цены" находится в пределах спрэда, то и вовсе невозможна.
Конечно. Я уже выше это отмечал.
все верно. Но плановый TP зависит от временного горизонта во многом.
Однозначно. Только не соглашусь насчёт SL. Несмотря на статпреимущество, выбросы против нас вовсе не исключены, в том числе и сильные. Мы должны либо уменьшать долю капитала в игре, либо защищаться от маржинколла стопом. То есть появляется предмет для оптимизации.
...
мы вправе предположить наличие резкой границы справа у ФР взяток оптимальной ТС. Это требование связано, как я уже отмечал, с наличием двух конкурирующих процессов влияющих на профитность ТС - частоты совершения транзакций и их амплитуды.
Здесь мне трудно согласиться, по крайней мере с ходу. Фактически ты говоришь здесь о той или иной форме принудительного закрытия позиций по времени. Такое закрытие даст не резкое обрезание, а скорее постепенное подавление хвостов.
Хорошо, резкое обрезание можно считать аппроксимацией этого подавления. Но временем будут давиться оба хвоста, ведь большие убытки также связаны со временем, как и большие профиты.
Однозначно. Только не соглашусь насчёт SL. Несмотря на статпреимущество, выбросы против нас вовсе не исключены, в том числе и сильные. Мы должны либо уменьшать долю капитала в игре, либо защищаться от маржинколла стопом. То есть появляется предмет для оптимизации.
Смотря для какого из 3х вариантов. Когда длина серии известна заранее, то эфективен способ выбора величины ставки - опять же в зависимости от длины серии и без использования SL. Если длина серии заранее неизвестна, то SL имеет смысл и тогда лот будет выбираться в от его величины. Или наоборот - размер ставки - выбор SL. Т.е. только в связке размер ставки-SL.
Но это абстрактные примеры, на практике SL нужен, т.к. реальное распределение цен нестационарно и вместо стат. преимущества после входа, можно получить стат. убыточность через некоторое время/после некоторого события. Именно их пытается отсечь SL
Neutron писал(а) >>
Вот и давай, выбирай себе самую широкую постановку и покажи как нужно. Мы поучимся. А пока, чё могём, то и творём.
тема выставления SL, для меня очень интересна, и пока открыта, вот я тут и пристаю к тебе с вопросами. И разумеется этим займусь в самое ближайшее время, но не в плане кого то "научить", а в смысле решить этот вопрос для своих, выработанных принципов торговли. И конечно надеюсь, что будет получена некая общность в узком смысле. :о)
Смотря для какого из 3х вариантов. Когда длина серии известна заранее, то эфективен способ выбора величины ставки - опять же в зависимости от длины серии и без использования SL. Если длина серии заранее неизвестна, то SL имеет смысл и тогда лот будет выбираться в от его величины. Или наоборот - размер ставки - выбор SL. Т.е. только в связке размер ставки-SL.
Но это абстрактные примеры, на практике SL нужен, т.к. реальное распределение цен нестационарно и вместо стат. преимущества после входа, можно получить стат. убыточность через некоторое время/после некоторого события. Именно их пытается отсечь SL
А по-моему, когда длина серии известна, то как раз удобно на основе статистики выбирать для нее SL, исходя из принятой для себя меры риска. Выход за рамки этой меры воспринимается как неожиданно большой выброс против позиции и закрывается по SL.
А по-моему, когда длина серии известна, то как раз удобно на основе статистики выбирать для нее SL, исходя из принятой для себя меры риска. Выход за рамки этой меры воспринимается как неожиданно большой выброс против позиции и закрывается по SL.
так и есть в реальных задачах. То что я описал было для монетки с неизменными вероятностями
Но существует и вторая ось координатной плоскости, где разыгрываются наши события, - ценовая, и связь между ними однозначная. Согласно выше приведённой формуде, амплитуда цены V(t) и время t в течении которого эта амплитуда наигрывается связаны следующим выражением:
Предположение об однозначности связи выглядит неоправданно сильным, реально эта связь статистическая. Но даже в приближении однозначной связи эта формула будет относиться как к движениям "за нас", так и к движениям "против нас".
Поэтому, имхо, корректно ввести асимметрию можно только введя дополнительные условия. Например для данного случая это будет "режь прибыль, давай убытку расти". В общем для отдельного рассмотрения вопроса о SL можно зайти и с этой стороны, но это нужно оговорить. Имхо, разумеется.
Предположение об однозначности связи выглядит неоправданно сильным, реально эта связь статистическая. Но даже в приближении однозначной связи эта формула будет относиться как к движениям "за нас", так и к движениям "против нас".
Поэтому, имхо, корректно ввести асимметрию можно только введя дополнительные условия. Например для данного случая это будет "режь прибыль, давай убытку расти". В общем для отдельного рассмотрения вопроса о SL можно зайти и с этой стороны, но это нужно оговорить. Имхо, разумеется.
Незнаю... Пока в голову по этому моменту ничего не лезет.
Вернёмся к анализу ФР оптимальной ТС (ОТС, а то уже достало выписывать одно и то же:-).
Из рис. видно, что мы имеем две степени свободы в определении местоположения ФР - её можно двигать враво-влево и менять крутизну склона (рис. слева):
Причём, за изменение крутизны отвечают зависимости в ценовом ряде. Поскольку вариантов всего два (круче-положе), то можно предположить, что эти два варианта соответствуют каким-то двум основным немартингальным свойствам Рынка... Правильно! - сто пудов, это или тренд, или флет (третье устойчивое состояние - мартингал). На мартингале интеграл от ФР в бесконечных пределах должен дать ноль. Это понятно. На реальном ценовом ряде, мы получим МО>0 или MO<0, и можно торговать, правда в последнем случае нам для получения положительного профита, придётся "перевернуть" ТС для того что бы МО стало вновь больше нуля (см. рис. справа). Положение вертикально обрезанной границы определяется, как я уже говорил, спредом и степенью предсказуемости рынка. Чем рынок более предсказуем, тем ближе эта граница к своему предельному значению H opt=2Sp. Чем более рынок напоминает мартингал, тем дальше эта граница отодвигается в область больши значений h и торговля становится всё менее эффективной.
Обращаю внимание на то, что до сих пор мы при построении ФР ОТС нигде специально не огаваривали вид закономерностей которые она может обыгрывать на рынки, принося нам тем самым профит. Зависимости во ВР, как мы знаем, бывают линейные и все остальные (нелинейные). Выявление линейных зависимостей в ценовых рядах задача непростая, но решаемая, а вот с нелинейными зависимостями труднее - их разнообразие бесконечно и унивесального отлавливателя для них нет (если, онечно, это не наша ОТС). Каждую нужно чётко идентифицировать, настроить под неё конкретный механизм и молится, что бы она (нелинейная зависимость) не поменяла ненароком какой нибудь коэффициент в 11 члене степенного ряда её описывающего:-) К чему это я? Так вот, наличие в ВР нелинейностей приведёт к появлению на ФР ОТС немонотонностей (я сейчас говорю о ТС без защитных ордеров) в виде плавных вздутий и утончений. Т.е., если линейные зависимости будут менять крутизну склона ФР, то нелинейные приведут к деформации, появятся, например, толстые хвосты и т.п. Ниже на рис. слева приведен пример линейной зависимости между соседними отсчётами в РПР :
Справа - очень нелинейная система:-)
Таким образом, мы имеем всего оди настраиваемый параметр в ТС - H opt и всего один параметр, который характеризует состояние рынка - крутизну наклона ФР. Последний параметр,судя по всему, слабо зависит от нелинейных особенностей ценообразования и ОТС таким образом претендует на целостность (в смысле максимально полного обыгрывания любых рыночных комбинаций).
P.S. Блин, пост предыдущий похерил...