Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Да нет не то получается. По этой формуле выходит что БГШ корелирован. Все время r лежит в районе минус 0.5
Вот проверочный код
Проверил.
Сергей, давай по-порядку.
1. Мы работаем с ВР аналогичным котиру. Такой ряд получается интегрированием СВ с нулевым МО. Пример СВ с нулевым МО:
dX=rnorm(n+1,0,10), где n+1 - число членов СВ имеющее гауссово распределение, 0 - МО равное нулю в моём случае, и 10-ти - в твоём примере, 10 - ширина этого распределения в моём случае и 100 - в твоём. Чтобы построить ВР аналогичный ценовому, мы должны проинтегрировать исходный ряд (найти его комулятивную сумму):
Вот, как выглядят распределения приращений интегрированной СВ (рис. слева) и сами приращения на фоне ВР (красная и синяя линии на правом рис.):
Сергей, именно свойства ВР (тот, что сининький) мы изучаем сейчас, а ты в своём посту подставил в формулу для расчёта коэффициента корреляции в ряде первой разности, саму первую разность (dX в моих обозначениях и Х - в твоих). Конечно, ты и получишь R=0.5 другого и не должно быть (доказывается элементарно). Так вот, если сейчас посчитать по предлагаемой мной формуле r для интегрированной СВ с нулевым МО (та, что сининькая на правом рис.), то получишь ожидаемый ноль:
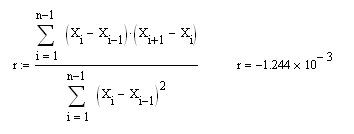
И, конечно, это то же самое, что и r для ряда приращений dX (но, по другой формуле):
Надеюсь, теперь у нас консенсус по данному моменту?
P.S. Можно и так:
Хорошо давай по порядку.
Сделал я то, про что ты говорил проинтергрировал СВ с МОЖ=0. Вот весь код
Вроде бы на первый взгляд все нормально. Но есть подводный камень. Подадим на вход формулы корелированный массив. В виде тренд + шум. y=a*x+b+rnorm(). Это можно просто сделать, задать вместа МОЖ=0, допустим 0.5
Из рисунка видно кто кривая (синая) явно корелирована. Разбив её на два массива А и В считаем коэффициент кореляции, он получаеться 0.993. А по твоей формуле 0.225.
Дело в том что по определению коэф.кореляции (КК) считаеться между двумя массивами. Ты же используеш один и тот же. Так можно делать сравнивать массив сам с собой. Это называется АКФ, т.е. формируються два массива А исходный, а второй B сдвинутый по времени относительно A и строиться график - зависимость КК от сдвига. Если сдвига нет, то КК естественно = 1. Вот график АКФ последней синей кривой.
Вот такое аппонирование получилось. Т.е. пока остаюсь при своем, что ты что то считаеш по этой формуле, но это не КК. Цифорки не сходяться ((
Но мы ушли всторону. Нужно сначала правильно херста посчитать, а уже потом смотреть чем он отличаеться от КК.
Вот интересная работа в которой производится анализ различных временных рядов
с использованием показателя Херста.
Из рисунка видно кто кривая (синая) явно корелирована. Разбив её на два массива А и В считаем коэффициент кореляции, он получаеться 0.993. А по твоей формуле 0.225.
Тут я не понял до конца.
На какие массивы ты разбил трендувый ВР? На прямую Y=a*X+b и случаную компоненту с нулевым МО, и между ними ищешь коэффициент корреляции?
Вот интересная работа в которой производится анализ различных временных рядов
с использованием показателя Херста.
Тут я не понял до конца.
Теперь понял.
Ты ищешь коэффициент корреляции между исходным ВР (не его приращениями) и им же, но сдвинутым на 500 отсчётов вправо. Т.е. ищится коэффициент корреляции между двумя всегда положительными ВР! Ну, конечно он будет положительным и очень большим (около 1) всегда.
Сергей, я тебя не понимаю! Что ты считаешь, коэффициент корреляции между исходным ВР и им же но сдвинутым? Нафик он нам нужен?! Нас интересует коэффициент корреляции между соседними отсчётами в ряде первой разности исходного ВР. Именно он показывает зависимость ожидаемого приращения от предыдущих. Именно этот оказатель идентичен Херсту сдвинутому на 1/2.
Спасибо. Посмотрим.
Тут похоже на правду.
Пробовал реализовать, но у меня получилось очень близко к 1 для курсов.
______________
Перечитал статью -- вроде наступил на грабли.
Для валютных пар показатель Херста вроде как надо считать для производной, я считал для курса.
Перечитал статью -- вроде наступил на грабли.
Мда:-)
Забегая вперёд.
Вот как выглядит ряд интегрированной СВ и курс EURGBP (рис.слева), а вот как выглядит амплитуды их приращений на разных ТФ в двойном логарифмитическом масштабе (рис.спарава), по оси абсцисс отложен логарифм ТФ:
Херс, утверждает, что тангенс угла наклона этих прямых равен 1/2 для случайной интегрированной величины (торговать на таком котире бессмыслено), меньше 1/2 для откатного рынка и больше 1/2 - для трендового. Посмотрим, чему равен этот угол для СВ. Тут можно, как советуется в статье, провести МНК прямую и найти её наклон, но я найду эту величину локально - проводя прямую через каждые две точки. В итоге получим ПХ для каждого ТФ:
Тут кружочками показан ПХ для СВ (красный цвет) и синим - для котира EURGBP по оси абсцисс отложен ТФ в мин. Крестиками показан коэффициент корреляции между соседними отсчётами для ряда первой разности исходных рядов со смещением 1/2. Коэффициент корреляции находился по формуле приведённой в первом сообщении этой странички. Видно, что согласие между двумя этими способами оценки предсказуемости ВР удовлетворительное, в то время как формулок в моём случае много меньше (всего одна). Что, собственно, и требовалось показать.
Кроме того, Случайный ряд дал ПХ=1/2 и r=0 (на рис. имеется смещение) как и следует из определения. Для котира явно видна откатная тенденция (антиперсистентность), тем большая, чем меньше ТФ.
Тут кружочками показан ПХ для СВ (красный цвет) и синим - для котира EURGBP по оси абсцисс отложен ТФ в мин.
Случайный ряд дал ПХ=1/2 и r=0 (на рис. имеется смещение) как и следует из определения. Для котира явно видна откатная тенденция (антиперсистентность), тем большая, чем меньше ТФ.
Наверное поэтому пипсовщики так любят еврофунт
Наверное поэтому пипсовщики так любят еврофунт
Это очевидно!
Это очевидно!
Из чистого любопытства - хотелось бы найти крайне персистентные пары,
или на худой конец условия при которых персистентность возникает):