- Ressonância estocástica
- uma estratégia comercial baseada na Teoria da Onda de Elliott
- Para os compradores e clientes de Expert Advisors (robôs comerciais), isto é dedicado.
O indicador i-regr pode fazer regressões polinomiais arbitrárias em qualquer grau. Eu nunca tentei nada acima do 3º grau, mas o código está lá para você olhar. O 6º grau provavelmente matará sua CPU, mas você pode tentar.
O indicador i-regr pode fazer regressões polinomiais arbitrárias em qualquer grau. Eu nunca tentei nada acima do 3º grau, mas o código está lá para você olhar. O 6º grau provavelmente matará sua CPU, mas você pode tentar.
Obrigado Rocketman! Não matou em nada minha CPU - vou trabalhar com isto por um tempo usando e ver o que consigo descobrir.
Atualização:
O i-regr não parece ter um alto grau de precisão - pode ser possivelmente devido ao método gauss (i-regr) e menos quadrados (excel) usados para resolver. Eu não sei - ainda procurando, alguém tem melhores procedimentos de politrabalho?
i-regr está trabalhando no valor Close[] de cada barra, o que provavelmente faz diferença (acho que você equalizou os comprimentos dos padrões em MT4 e se sobressai).
você pode mudar isso facilmente mudando Close[] para Open/High/Low ou para qualquer outra expressão analítica, por exemplo, função de peso.
No entanto, não acredito que você possa lucrar com isso, é como qualquer outro indicador de tendência de repintura.
Olá dennisj2,
você tem certeza de que realmente precisa de sua fórmula?
Talvez você tente primeiro procurar por outros filtros como Kalman, Ehlers, Gauss, Jurik (JMA), DEMA. A maioria deles deriva de filtros de baixa freqüência (física) e a maioria deles encontrou seu caminho para o código mt4.
Pode ser um JMA (há muitas variações) com um período mais longo - o que você está procurando?
Agora começa minha busca.
Agora que identifiquei uma aplicação prática, procurei aprender (ou, no meu caso, reaprender) a matemática por trás da fórmula da linha de tendência poligonal. Boa sorte com isso. É muito difícil (para mim) traduzir em código a redução mínima de quadrados e matrizes adicionadas à fórmula extremamente complexa e cálculos de coeficiente necessários introduzidos pela equação polinomial. Assim, achei que seria mais fácil chamar o Excel (provavelmente de c++), fornecer uma matriz de (x,y) valores de dados, calcular a interceptação polinomial (valor da linha de tendência) usando LINEST(), e retornar este valor de volta ao meu aplicativo desktop (um aplicativo de software proprietário fechado com funcionalidade limitada de chamada de saída).
A montagem da fórmula usando LINEST() tornou-se um obstáculo substancial. É suficientemente fácil fornecer os dados - mas, como posso calcular as interceptações (x,y) mostradas tão impecavelmente no gráfico? Cada nova medida muda a fórmula e usa os coeficientes recém-calculados? Por que isso acontece? Eu passei horas, horas e horas (e depois algumas) vasculhando a Internet em busca de soluções - e (assim como um homem) decidi finalmente pedir orientações.
Eu tenho os valores da fonte (anos após anos). O que me falta é a) o método para gerar a interceptação do poli(x,y), b) chamando o Excel externamente para c) devolver o poli(x,y) com base nos dados fornecidos (x,y) -
Se alguém tem um artigo ou tratamento muito específico deste tópico, ou mesmo disposto a dar uma mãozinha, eu ficaria para sempre em dívida para com você.
dj
Há muitos artigos por aí sobre álgebra com exemplos em grego, mas na verdade é vudu.
Por exemplo, há um artigo wikipedia sobre regressão linear que não faz nenhum sentido para mim, mas eu poderia codificar uma versão de regressão linear de sua linha agora mesmo porque em outro lugar eu aprendi a usar a fórmula
y=a+bx
No entanto, em nenhum lugar do artigo da wikipedia essa fórmula sequer é mencionada, como isso pode fazer sentido?
também aprendi ao usar essa fórmula
a == declive
b=== interceptar
a matemática para calcular a inclinação e interceptação é conhecida e é um procedimento bastante simples de cálculo das somas dos valores, quadratura de alguns deles, etc.
Também sei que a fórmula para uma regressão quadrática (2º grau) é y=ax^2 + bx + c
Portanto, penso que estão relacionados, o que deve significar que a equação para a regressão de 3º grau é
y=ax^3 + bx^2 + cx + d
então eu acho que a 6ª regressão seria
y=ax^6 + bx^5 + cx^4 + dx^3 + ex^2 + fx + g
mas se a é declive e b é interceptar o que é c e o que seria d etc. ? Essa é a única razão pela qual não consegui codificar sua linha, não sei quais são os coeficientes ou como calculá-los.
ATUALIZAÇÃO: ok, eu aprendi outra coisa que está me confundindo agora.
em outro artigo polinominal quadrático é descrito como
ax^2 + bx + c = 0
Isso significa que não precisamos saber nada de matemática para interceptar a inclinação e poderíamos resolver o quadrático para encontrar os valores de a, b e c ?
Mas como o ax^2 + bx + c = 0
relacionar-se com
y=ax^2 + bx + c ?
Eles parecem semelhantes, mas como um é y= e o outro é =0 ?
SDC,
a inclinação em um ponto pode ser calculada através da primeira derivação de uma função.
Uma função linear como y=ax+b tem em qualquer ponto a mesma inclinação: a.
Em geral, a derivação de uma função linear eixo^n + bx^n-1 + ... + z = y é simplesmente: nax^(n-1) + (n-1)bx^n-2 ... = y' - a última constante da função original torna-se 0, sempre!
Então ax + b = y => y' = a ( <= 1*a^(1-1); b=0 )e a função quadrática torna-se y' = 2ax + b ( <= 2ax^(2-1) + 1bx^(1-1); c=0 ).
Mas acho que para entender a idéia de filtros é melhor pensar (e ler) sobre as freqüências de filtragem. Não importa se é som ou imagens ou citações ou ...
Sempre se quer se livrar do ruído - em geral - as freqüências de curto prazo. E o uso de funções lineares é apenas uma abordagem.
Obrigado por tentar me explicar isso, mas não sei por que essas equações significam o que significam. Se eu souber calcular os coeficientes individualmente de forma processual, posso usá-los e ligar os valores, mas é só isso.
Eu entendo o conceito de filtros, eu só estava interessado em descobrir como codificar a linha da OP.
Mas em relação a fazer isso, quando você diz,
"So ax + b = y => y' = a ( <= 1*a^(1-1); b=0 )e a função quadrática torna-se y' = 2ax + b ( <= 2ax^(2-1) + 1bx^(1-1); c=0 )".
Eu não faço idéia do que você está falando ou mesmo como isso é relevante, então eu provavelmente não estarei fazendo nenhuma codificação de linhas de poli em breve rs
SDC:
Há muitos artigos por aí sobre álgebra com exemplos em grego, mas realmente é vudu.
SDC - agora você está no mesmo nível que eu - a fórmula de regressão linear que encontrei funciona - e há duas fórmulas distintas que encontrei e que produzem resultados idênticos. Estas fórmulas são ótimas se a regressão linear (uma linha reta de tendência) é o que procurávamos.
Em primeiro lugar, algum material de referência:
Microsoft: http://office.microsoft.com/en-us/excel-help/linest-HP005209155.aspx
IntegralCalc: https://www.youtube.com/watch?v=1pawL_5QYxE&noredirect=1
Dada a equação de regressão linear y = mx + b:
Onde y = preço, (por exemplo, Close[x])
e x = índice (por exemplo, Bar[x])
e m = Declive (o coeficiente aplicado a cada par (x,y))
e b = intercepção Y (o valor base da intercepção Y aplicado a cada par (x,y))
Método A: De IntegralCalcMétodo B: Da Microsoft (onde x(overbar) e y(overbar) são meios)
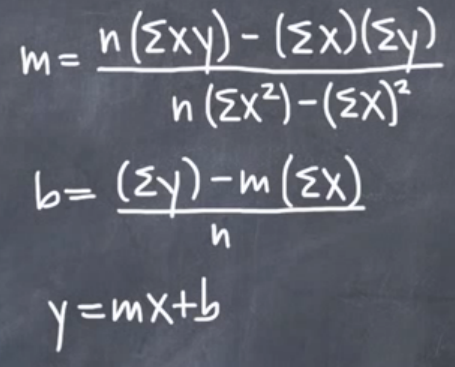
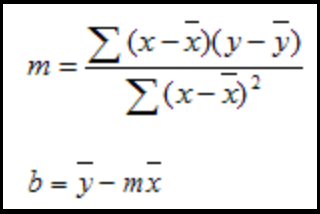
Mesmo a fórmula da linha de tendência de regressão polinomial até o nono grau é relativamente fácil de aplicar:
Dada a fórmula: y = m1*x1 + m2*x2 + m3*x3 + ... + b
Onde as variáveis x, y, m, e b levam a mesma definição descrita na equação linear.
Parece que eu tenho tudo, então o que está faltando?
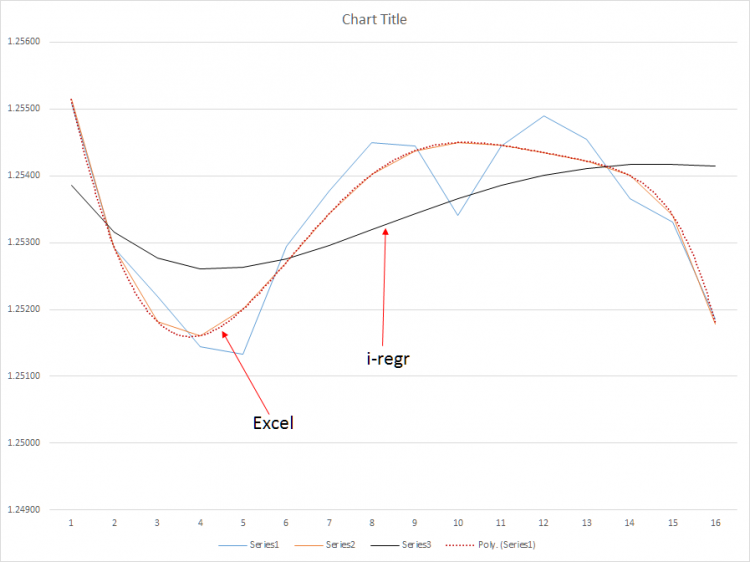
O que está faltando é o cálculo para o m (Slope) e o b (Y-intercepção) para uma regressão polinomial; a equação linear para o cálculo destes valores não se aplica a uma regressão polinomial. Pelo que aprendi, a regressão polinomial requer uma fórmula que calcule os mínimos quadrados com base em um sistema de equações polinomiais usando uma matriz. Veja os gráficos de exemplo acima. No primeiro gráfico, as linhas de polinômio(6) são absolutamente imaculadas - tops e bottomtoms são claramente chamados de fora. Com estes dados, serei capaz de manter as negociações por mais tempo do que faço hoje, em última análise dobrando, potencialmente triplicando minha média de pips por negociação.
No segundo gráfico, mostro os resultados do método poly(6) versus o método i-regr que usa uma matriz de gauss para resolver os coeficientes de inclinação - e, escusado será dizer, é bastante inútil devido à latência substancial do método. Por outro lado, uma simples média móvel é ainda pior - o SMA é muito sensível durante correções intermediárias de mercado que poderiam causar uma reação exagerada do meu EA.
Estou disposto a pagar alguém para desenvolver um verdadeiro indicador de regressão polinomial - mas, os resultados devem absolutamente espelhar os resultados que o Excel produz. A função LINEST() é uma caixa preta onde muito voodoo é usado para calcular os coeficientes. Muito simplesmente, eu preciso entender este vudu.
Atualização: anexei um arquivo mostrando o método implementado no Excel.
i-regr está trabalhando no valor Close[] de cada barra, o que provavelmente faz diferença (acho que você equalizou os comprimentos dos padrões em MT4 e se sobressai).
você pode mudar isso facilmente mudando Close[] para Open/High/Low ou para qualquer outra expressão analítica, por exemplo, função de peso.
No entanto, não acredito que se possa lucrar com isso, é como qualquer outro indicador de tendência de repintura.
Grazi -
Eu usei o i-regr e comparei os resultados acima - o algoritmo Poly(6) vs. i-regr mostra que o i-regr tem uma latência substancialmente maior que o poly(6) baseado no mesmo conjunto de dados - latência é a morte neste mercado. Meus EAs não negociam oscilação intradiária, mas sim, mantêm a tendência. Portanto, você está enganado - eu lucro com meus EAs e, com um indicador reativo mais lento, meus EAs vão capturar mais do mercado do que eles capturam hoje. Especificamente, uma vez que eu tenha integrado um verdadeiro algoritmo poly(6), terei a capacidade de manter posições abertas por mais tempo e prever mudanças de tendência 3-4 períodos antes, melhorando meus pontos de entrada.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso