Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Если приращения случайны, то цена - это random walk, она имеет нормальное распределения, и заработать на ней гарантированно нельзя.
Однако надо оговорить природу приращения, сказать просто "случайная" - не сказать ничего. В жизни всё случайно. У автобуса есть расписание, но время его прибытия величина случайная. Случайные приращения цены могут быть коррелированы с фазами луны, например, это не делает их неслучайными.
Чтобы получить random walk приращения должны быть iid независимыми и одинаково распределёнными.
O problema é esse: o aumento de preço não é normalmente distribuído. Caso contrário, seria garantido ganhar dinheiro com isso.
В том то и дело, что приращение цены не нормально распределено. Иначе заработать на нем было бы гарантированно можно.
em relação a quais são os incrementos anormais?
В том то и дело, что приращение цены не нормально распределено. Иначе заработать на нем было бы гарантированно можно.
O aumento de preço pode ser assumido como sendo normalmente distribuído, o que está suficientemente próximo da realidade, mas não faz nada se for iid . O aumento de preço pode ser considerado como distribuído em t com graus de liberdade 4 ou 5. Isto é muito mais próximo da realidade do que assumir que os incrementos são normais.
O processo resultante será uma caminhada aleatória. É garantido que será distribuído normalmente independentemente da distribuição dos incrementos, mas a normalidade não ajuda - não se pode ganhar dinheiro em uma caminhada aleatória. Os aumentos de preço podem ser considerados estacionários, mas não podem ser comercializados. Você pode negociar o preço, e é uma caminhada aleatória, um processo não estacionário. Pelo menos no contexto deste tópico.
Приращение цены можно считать нормально распределённым - это достаточно близко к реальности, однако это ничего не даст, если оно iid . Можно считать приращение цены t-распределённым со степенью свободы 4 или 5. Это гораздо ближе к реальности, чем допущение о нормальности приращений.
Результирующий процесс будет random walk. Вот он-то вообще гарантированно нормально распределённый, независимо от распределения приращений, но от той нормальности никакого прока - нельзя заработать на случайном блуждании. Приращение цены можно считать стационарными, но их нельзя торговать. Торговать можно цену, а она random walk, процесс нестационарный. По крайней мере в контексте данного топика.
Posso discutir um pouco para manter a discussão? Não estou muito certo do que quero dizer agora. Especialmente agora, é muito tarde. Mas ainda assim... Se os incrementos de alguma quantidade são normalmente distribuídos, isso significa que essa quantidade é limitada. (Será que estou errado?).
A menos que a afirmação anterior esteja errada, há um valor máximo e um valor mínimo no conjunto de valores de uma quantidade. Além disso, quanto mais próximo o valor de um valor estiver do máximo ou mínimo, maior é a probabilidade de que ele mude para a média. Esta é a lei que pode ser usada.
p.s. Não pense que eu estou atacando. Só quero ter uma conversa com uma pessoa inteligente.
Можно я для поддержания дискуссии немножко поспорю? Я сейчас сам не очень уверен в том, что хочу сказать. Тем более уже очень поздно. Но все-таки... Если приращения какой-то величины нормально распределены, то это значит, что эта величина ограничена. (Ошибаюсь?)
Если не ошибся в предыдущем утверждении, то во множестве значений величины есть максимумальное и минимальное. Кроме того, чем ближе значение величины к максимальному или минимальному, тем больше вероятность его изменения в сторону среднего. Вот это и есть закон, который можно использовать.
п.с. Не подумайте, что я нападаю. Просто хочу поговорить с умным человеком.
Você não ouviu falar do teorema do arcsine e do erro do jogador?
Não perguntei sobre a relatividade da deflexão por nada.
Se ele retornar - uma canção.
MA(x período) é uma música diferente...
Se você usar TrueDMA em vez de MA - uma cacafonia completamente diferente acontecerá com você.
;)
Onde você obteve a anormalidade?
Não pergunte a ninguém, eles não dizem uma palavra.
Há um tópico - ele mostra o oposto.
Yo meu...
:)
Можно я для поддержания дискуссии немножко поспорю? Я сейчас сам не очень уверен в том, что хочу сказать. Тем более уже очень поздно. Но все-таки... Если приращения какой-то величины нормально распределены, то это значит, что эта величина ограничена. (Ошибаюсь?)
Если не ошибся в предыдущем утверждении, то во множестве значений величины есть максимумальное и минимальное. Кроме того, чем ближе значение величины к максимальному или минимальному, тем больше вероятность его изменения в сторону среднего. Вот это и есть закон, который можно использовать.
п.с. Не подумайте, что я нападаю. Просто хочу поговорить с умным человеком.
Você está definitivamente errado. A natureza da distribuição não diz nada sobre a limitação do valor. Provavelmente existem algumas exceções, mas em geral este é o caso. As limitações são impostas pelos parâmetros da distribuição. Por exemplo: a prevalência normalmente distribuída é ~N(0,1). É um processo estacionário, tem limites de magnitude, quase nunca chegará a 4 ou -4.
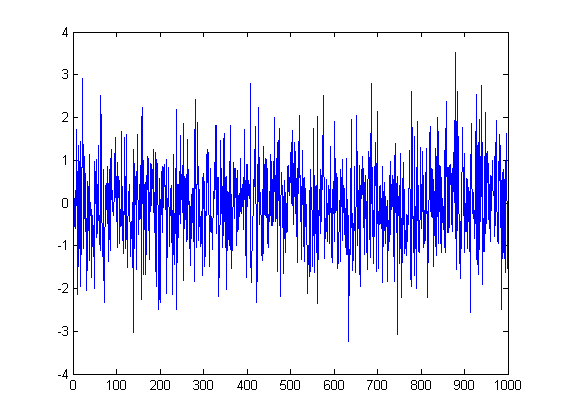
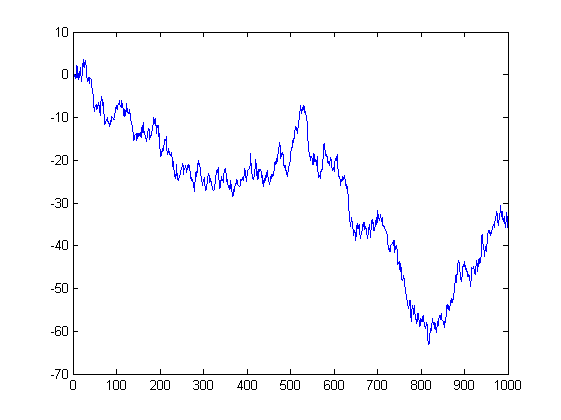

E aqui está o preço que sai desses incrementos. É uma caminhada aleatória. Ela também tem uma distribuição normal ~N(0,sigma^2), mas seu parâmetro de variância não é uma constante, mas aumenta com o tempo, ou seja, o número de incrementos. Naturalmente, este processo não tem limite de tamanho e visitará todos os pontos com igual probabilidade. Esta é a base do problema de falência do jogador - se você jogar por tempo suficiente em um jogo perfeitamente justo (50:50), você ainda perderá, porque mais cedo ou mais tarde esta curva o levará a um nível mais baixo do que você tem dinheiro.
E aqui estão 1.000 caminhadas aleatórias, você pode obviamente ver o sino da distribuição normal.
Mas o que você diz sobre o retorno ao meio é uma história diferente, é um processo de reversão do meio - autoregressivo (AR)
x(i) = a * x(i-1) + e(i). A transformação e(i) é ~N(0,1), a < 1.
Se você encontrou um processo negociável de reversão de meio, então só há tempo para transportar cestas de repolho. Naturalmente, depende dos parâmetros - a taxa de retorno à média (a) - mas de qualquer forma é legal.
А вот 1000 случайных блужданий, очевидно виден колокол нормального распределения.
você tem que iluminar as freqüências dos acertos.
--
o duplo King(log) Bell em expansão.
;)
не всякий увидит.
Você tem um histograma e um gráfico de probabilidade para a 1000ª amostra.


Embora, como os incrementos foram normais, a soma das distribuições normais é uma distribuição normal. Você não precisa nem mesmo verificar nada.
На тебе гистограмму и пробабилити плот для 1000-го отсчёта.
Хотя исходя из того, что приращения были нормальные, сумма нормальных распределений есть нормальное распределение. Тут ничего даже и проверять-то не надо.
Sens!
Bom (ou melhor - e visualmente útil;) trabalho.