Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Если параметры распределений Б и С различны, то формулы для вычисления МО и дисперсии будут сложнее, но все равно будет такое же распредление
Isto se C e B tiverem uma distribuição estável. Nesse caso, sim, a soma das distribuições estáveis é igual a uma distribuição estável. Caso contrário, não, a soma ou diferença de C e B com distribuições diferentes terá uma distribuição infernal.
Если оба процесса независимые, то оба они просто шум. Если ты складываешь или вычитаешь два шума, то получаешь просто третий шум. Т.е. результирующий процесс будет
y(i) = y(i-1) + e(i), где e(i) = b(i)+s(i) или e(i) = b(i)-s(i); + или - это не имеет значения.
Случайное блуждание чистой воды. Мелкие модификации, типа типа обрезания паникёров, серьёзно ничего не изменят. Только если твои процессы будут не независимые, то могут начаться чудеса.
Obrigado por sua resposta.
Posso introduzir mais uma emenda ao algoritmo?
Se o herói teve seu "incremento" - seus poderes e dúvidas são duplicados.
Como seria então este processo praxiológico aleatório?
Sabendo o que você modelou de maneira semelhante - você pode olhar para o sino/pipe?Isto se C e B tiverem uma distribuição estável. Nesse caso, sim, a soma das distribuições estáveis é igual a uma distribuição estável. Caso contrário, não, a soma ou diferença de C e B com distribuições diferentes terá uma distribuição infernal.
Estamos falando da modelagem de caminhadas aleatórias, que geralmente é feita com distribuições estacionárias - normais ou discretas. Poderíamos provavelmente trabalhar em torno dela e modelá-la como não-estacionária. A soma ou diferença de distribuições não estacionárias também será, como regra, não estacionária, embora haja exceções que estão subjacentes à cointegração, por exemplo
Спасибо за ответ.
можно ввести еще одну поправку к алгоритму?
Если герой получил свое "приращение" - его силы и сомнения удваиваются.
Как тогда этот случайно праксиологический процесс будет смотреться?
Зная, что вы похожее моделировали - можно колокол/трубу глянуть?Realmente não entendo. Como y(i) = y(i-1) + e(i) * i, onde e(i) = b(i)+s(i)?
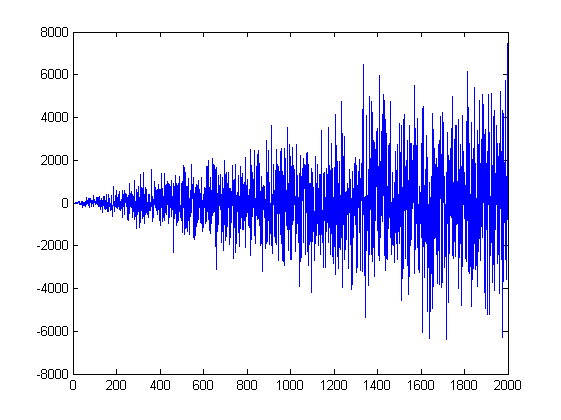
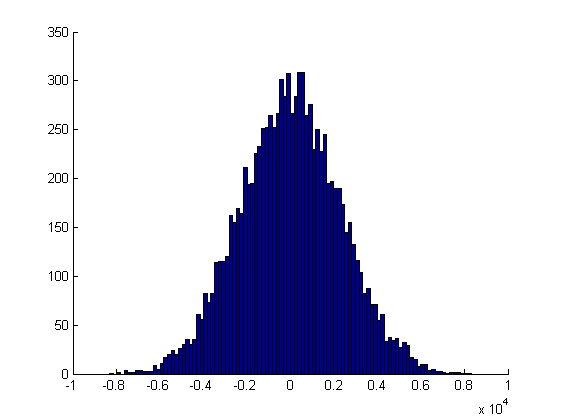
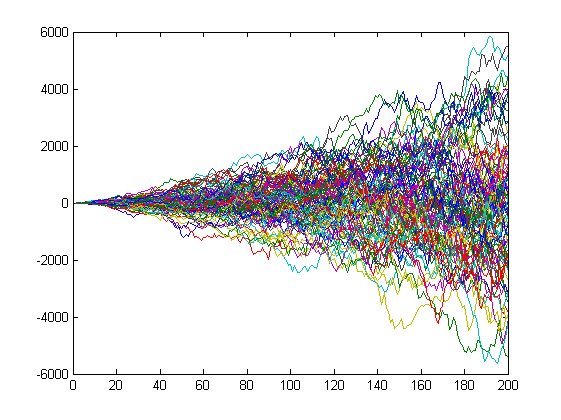
Não dobrando, mas aumentando. A duplicação vai crescer muito rápido. Mesmo uma simples multiplicação por i dá este crescimento de incrementos
Entretanto, o processo resultante y(i) permanece normal, o que é o que esperamos de uma caminhada aleatória.
Embora possa não parecer assim à primeira vista, isto se deve apenas à mudança de escala
Не очень понял. Типа y(i) = y(i-1) + e(i) * i, где e(i) = b(i)+s(i)?
Не удваивается, но возрастает. Удваивание слишком быстро вырастет. Даже простое умножение на i даёт вот такой рост приращений
Однако, результирующий процесс y(i) остаётся нормальным, чего мы и ожидаем от случайного блуждания.
Хотя оно так может и не кажется на первый взгляд, но это только из-за изменения масштаба
Sobre dobrar é a seguinte observação "prática".
Se no passo anterior o herói obteve o incremento desejado (isto é, |y(i)-y(i-1)|>= força do herói no passo i-ésimo, então sua força gerada (incluindo menos - dúvida) no passo i+1 deve ser duplicada.
Aqui o arcseno deve se ampliar, mas não tenho certeza. O sinal-variância atrapalha;)
---
Um pedido atrevido - aumentar a duração da implementação para 500. fogo
На форуме часто в пылу дискуссии утверждается, что блуждание цены абсолютно случайно.
Пускай не всегда. Но случайность и не... сложно якобы отличить.
Теоремы арксинуса и двойного логарифма периодически обсуждаются или цитируются напрямую, либо только выводы.
Мутно как то...
У меня вопрос к теоретикам и практикам.
Изучал ли кто "блуждание после соударения"?
Постановка задачи следующая - есть два условных героя "БАЙ" и "СЕЛ".
Пускай генерится некое приращение для каждого из них.
В зависимости от героя назовём их "наступательным приращением" и "оборонительной силой".
...
Deve haver aqui uma nota de rodapé: se o incremento for ofensivo, ele deve, por convenção, ter precedência sobre os incrementos defensivos de mobilidade,
Ou uma constante deve ser adicionada ao RPM após a geração ou uma faixa de RPM deslocada deve ser definida.
Então, alguns atacam e outros defendem, caso contrário, como saberemos quem está na defensiva?
Sobre dobrar é a seguinte observação "prática".
Se no passo anterior o herói obteve o incremento desejado (isto é, |y(i)-y(i-1)|>= força do herói no passo i, então sua força gerada (incluindo menos - dúvidas) no passo i+1 deve ser duplicada.
Aqui o arcsine deve amplificar-se, mas não tenho certeza. O sinal-variância atrapalha;)
Você espera determinar (ou melhor, encaixar) a distribuição do mercado através de tal adivinhação de folhas de café?
супер!
О удваивании следующее "прак...ое" наблюдение.
Если на предыдущем шаге герой получил желаемое приращение (т.е |y(i)-y(i-1)|>= сила героя на i-том шаге, то его сгенерированную силу ( в том числе с минусом - сомнения) на i+1 шаге следует удвоить.
Não vale a pena. Tal manipulação mudará a distribuição dos incrementos, fará crescer grandes caudas, mesmo se B e C fossem normalmente distribuídas, mas não mudará a natureza do processo resultante - ainda será uma caminhada aleatória e será normalmente distribuída. Uma caminhada aleatória não se importa com a distribuição dos incrementos desde que o terceiro momento seja zero, ou seja, seja, é simétrica.
речь о моделировании случайных блужданий, что делается как правило стационарными распределниями - нормальным или дискретным. Можно наверное изголиться и смоделировать нестационарным. Сумма или разность нестационарных распределений будет так же нестационарна как правило, хотя есть исключения, которые лежат в основе коинтеграциии например
Não confundir calor e suavidade, ou seja, estacionaridade com distribuição. Eles não estão relacionados de forma alguma. Uma caminhada aleatória tem uma distribuição normal, mas não é estacionária. Uma distribuição uniforme é estacionária, mas a soma de duas distribuições uniformes não será uma distribuição uniforme. Esta é uma propriedade (para manter o tipo/formato da distribuição sob qualquer manipulação linear) apenas de distribuições estáveis.
Não confundir calor e suavidade, ou seja, estacionaridade com distribuição. Eles não estão relacionados de forma alguma. Uma caminhada aleatória tem uma distribuição normal, mas não é estacionária. Uma distribuição uniforme é estacionária, mas a soma de duas distribuições uniformes não será uma distribuição uniforme. Esta é uma propriedade (para manter o tipo/formato da distribuição sob qualquer manipulação linear) apenas de distribuições estáveis.
Como isso não está relacionado? A distribuição normal é estacionária e os incrementos da SB distribuídos pela NR são estacionários, e eu estava originalmente falando sobre os incrementos.
Em relação à própria SB (como soma cumulativa de incrementos): não haverá "rabos pesados", como você descreveu no post anterior. Porque a própria SB no tempo t também é normalmente distribuída, mas com uma variação t vezes maior do que para um único incremento (no tempo t desde o início da referência). Sim, a variação da distribuição da SB aumenta à medida que o tempo aumenta. Caudas pesadas acima de 3 sigmas, por exemplo, mas para SB se você calcular a variância em um determinado momento (e você pode fazê-lo analiticamente) será como se fosse normal.
Concordo que o processo SB em si não é estacionário, é um processo degradado com raiz unitária I(1), ou seja, as primeiras diferenças (incrementos) são distribuídas estacionárias https://www.mql5.com/go?link=http://window.edu.ru/catalog/pdf2txt/141/28141/11363?p_page=55 Mas uma distribuição não estacionária não tem necessariamente rabos pesados e, neste caso, não haverá nenhuma
Você acha que a HP é não-estacionária? Ou você não pode dizer para cada distribuição contínua se ela é estacionária ou não? :)