Etiqueta de mercado ou boas maneiras em um campo minado - página 57
Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Aqui vamos nós novamente com o OTO do mercado. O fato é que há um atraso, é claro, porque o meio do bar vem imediatamente após sua abertura, mas, por outro lado, ele não existe, porque quando o bar já está formado, não nos importamos quando exatamente dentro do bar chegou esse meio dourado. Já vi barras que começam e terminam no meio. A essência de sua discussão com o Neutron não vale uma única palavra. É porque as barras não são barras para o Neutron, porque um quociente não é quantificado pelo tempo, enquanto uma barra é um BAR para você.
Você tem diferentes "quadros de referência" - isso é tudo que existe.
Não, não velho... >> oh, Superstar!
Você ainda está sendo tola, minha querida? A velhice realmente não é divertida.
Aqui vamos nós novamente com o OTO do mercado. O fato é que há um atraso, é claro, porque o meio do bar vem imediatamente após sua abertura, mas, por outro lado, não existe, porque quando o bar já está formado, ninguém se importa quando este meio dourado dentro do bar já chegou. Já vi barras que começam e terminam com o meio. A essência de sua discussão com o Neutron não vale uma única palavra. É porque as barras não são barras para o Neutron, porque um quociente não é quantificado pelo tempo, enquanto uma barra é um BAR para você.
Você tem diferentes "quadros de referência" - isso é tudo que existe.
A discussão é sobre muitas coisas, esta em particular. Sergei fez um argumento "convincente" para isso. Mas parece que eu não sou capaz de explicar uma coisa simples. Não há atraso, não há nenhum atraso. Não pode estar lá por definição. Os dados sobre os quais estes números são derivados não se sobrepõem. Não há nenhuma fase, os números são exatamente iguais.
Adendo: É como tomar dois pontos em uma onda sinusoidal e dizer que em x em incrementos de 0,1 e em x em incrementos de 10,0 há um atraso.
Tudo bem - vamos manter a nossa opinião...
Experimente.
Portanto, boa sorte :). A decomposição da série Taylor é ainda pior do que em harmônicos porque um polinômio de grau não-zero não tem uma faixa limitada de valores.
Além de suas palavras, não se trata de um polinômio, mas de um aceno normal de SMA.
Muito bem, então. Aqui está a idéia em si. Se você pensar bem, não há força de mercado que subestime a importância dos 2º, 4º e 11º bares em comparação com os bares vizinhos. Ou seja, deve-se esperar que os bares vizinhos tenham valores muito próximos. O que aconteceu há 11 horas é tão importante quanto o que aconteceu há 12 horas. Portanto, devemos esperar uma transição suave em pesos de um bar para seus vizinhos. Portanto, a curva que descreve o peso em função do número de barras (atraso) deve ser suave. Se isto for verdade, esta curva pode ser aproximada por uma série Taylor, ou seja, por um polinômio. Você pode, por exemplo, ajustar um polinômio de 3º ou 4º grau a seus pesos. A próxima suposição da minha idéia é a seguinte. Ao invés da otimização dos próprios pesos (você tem 16 deles), otimize os coeficientes polinomiais (a0+a1*n+a2*n^2+a3*n^3, você otimiza a0...a3, você obtém 4 parâmetros no total), e use a fórmula a0+a1*n+a2*n^2+a3*n^3 para n-ésima barra. Muito menos cálculos. Experimente.
Sou sinceramente grato a vocês pela idéia, porém, uma vez na minha infância ouvi (dos meninos no hall de entrada), que se um erro for encontrado na fundação do conceito, todas as outras construções podem ser desconsideradas, independentemente de sua atratividade científica. Você tem um erro na idéia de lisura como uma função necessária para a transição de um (estado de mercado) para outro. Ai de mim. Devo decepcioná-los. as transições de mercado de A para Z sem reverência intermediária. Caso contrário - não seria um fórum, mas uma reunião de Soros.
Não importa... Vou lhe dar uma nova idéia (conceito de mercado), certamente mais frutífera do que a que você teve até agora:
É bastante simples à primeira vista:
A regularidade é uma maneira de existir a aleatoriedade. O oposto não é verdade.
ao Neutron
O produto não funcionará com este sistema operacional
foi buscar sabão...
A propósito, eu também posso prever assim. Mesmo sem um AR. :) Mas isso não me deu nada. Posso adivinhar "para onde" o preço irá com uma precisão de 80%, mas não tenho LUCROS. É triste. ;)
A série (H+L)/2. Denoto-o por Mu para brevidade. Suponha que não podemos prever com precisão este valor, mas podemos prever com precisão o sinal de diferença Mu(n)- Mu(n+1). Por exemplo, para a barra atual, sabemos que o próximo delta Mu(n) - Mu(n+1) será positivo. Então precisamos estimar estatisticamente o novo incremento e a partir dele ir para Mu(n+1). Vamos adicionar a estimativa RMS para o spread da barra a este nível. Obtemos um nível comercial e eu até desenhei um quadro para melhorar a expressão artística:
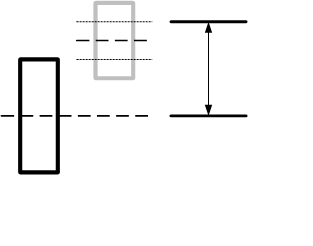
Se as freqüências de ocorrência desses níveis forem grandes e proporcionais à propagação, poderemos ser bem sucedidos. Você está realmente prevendo este delta em 80%?
PS: Eu pessoalmente não trabalho tão próximo do preço. Não há muitas chances, ou melhor, não há nenhuma chance. Acabei de ter a idéia de que de fato é possível prever não precisamente, apenas na direção. Fiz minhas próprias previsões com tal "tecnologia": "Você já viu este quadro?" pelo menos durante 24 horas em barras de 15 minutos, aqui estão exemplos de previsões reais, vou terminar os próximos testes - haverá mais (apenas depuração, nem todo o astrolábio foi construído ainda):
Teste de sistemas de previsão em tempo real
para gpwr
Sim, de alguma forma senti falta de seu penúltimo posto. Há uma pergunta interessante aqui: o que o faz pensar que o peso (em princípio) pode ser uma função de seu próprio índice a partir do tempo? Acho que entendo a origem de sua idéia - você está olhando para gráficos de pesos. Há uma sutileza: em duas experiências diferentes (resultados de treinamento no mesmo vetor de treinamento) estes gráficos (visualmente e topologicamente) podem ser significativamente diferentes, enquanto os resultados da grade (estatisticamente) são substancialmente os mesmos. Se você conseguir até mesmo encontrar uma funcionalidade satisfatória para o treinamento da rede pelo método proposto, os resultados do treinamento (duas experiências consecutivas no mesmo vetor) serão completamente idênticos - ou seja, não será uma rede neural, mas algo completamente determinístico. Como diria Neutron, que já está dormindo, tal rede será exatamente treinada para um vetor, mas não será capaz de compor poemas. Conseqüentemente, não tem nenhuma utilidade no comércio. Cada contagem sucessiva não é semelhante à anterior (e às novas), e uma grade normal não conta nem mesmo com isso. Ela se assemelha mais ou menos a alguma imagem que aprendeu. Se para substituir aproximadamente por exatamente, a entropia de tal rede será igual a zero (ou seja, um passo para a esquerda, um passo para a direita - pelotão de fuzilamento, um salto no local - provocação).
Entre outras coisas, não vejo diferença especial na velocidade de treinamento pelo método sugerido por você, pois para mudar um coeficiente de polinômio vou precisar exatamente dos mesmos recursos, como para corrigir um peso, e há n coeficientes (para cada peso), então qual é o ganho?
A série (H+L)/2. Denoto-o por Mu para brevidade. Suponha que não podemos prever com precisão este valor, mas podemos prever com precisão o sinal de diferença Mu(n) - Mu(n+1). Por exemplo, para a barra atual, sabemos que o próximo delta Mu(n) - Mu(n+1) será positivo. Então precisamos estimar estatisticamente o novo incremento e a partir dele ir para Mu(n+1). Vamos adicionar a estimativa RMS para o spread da barra a este nível. Obtemos o nível comercial e até fiz um desenho para melhorar a expressão artística:
Se as freqüências de ocorrência desses níveis forem grandes e proporcionais à propagação, poderemos ser bem sucedidos. Você realmente prevê este delta em 80%?
Surpreendido ao ver o algoritmo que demonstra isto mesmo 80%. Estou procurando por um erro. Parece muito simples. Não funciona dessa forma.
а-а-а-а-а-а-а-а-а-а-а-!!!!! Precisamos ver onde está a lua, talvez seja essa a razão. Agora eu entendo a expressão - "faltam palavras" É aí que está o atraso????
Construiu-o especialmente para você:
Você pode ver claramente que a FZ está sempre lá e é visualmente visível nos movimentos bruscos do kotir.
Você pode ver que o atraso está sempre lá, e é fácil de localizá-lo visualmente sobre os movimentos bruscos do kotir. Aprenda a matemática, e da próxima vez que você tiver a próxima idéia super-duper brilhante, para a implementação da qual você acha que precisa de um ou dois institutos de pesquisa e um cluster de PCs, você pensa por um minuto - talvez você simplesmente não saiba ou não entenda. Afinal, isto é mais provável que uma "descoberta marcante", em uma área onde tudo foi pisoteado antes de você.
Proponho uma forma abreviada de descrever todas as escalas, neste caso, um polinômio. Aqui vou lhe mostrar com seu exemplo. Você aprendeu sua rede em um determinado vetor de entrada e obteve valores de todos os pesos w[n] onde n=0...15.
Acredito que o paralocus aponta muito justamente para você que sua idéia se baseia na hipótese não comprovada de estacionaridade dos processos de mercado alocados à NS. Somente no caso de sua confirmação podemos esperar alguma semelhança de estacionaridade dos pesos NS e conseqüentemente aplicabilidade do método de extrapolação para encontrar pesos sem treinamento de rede. Mas, se assim fosse, não reciclaríamos a grade a cada novo dado da BP, mas temos que fazê-lo, e este fato, embora indiretamente, mas fala a favor da não-estacionariedade dos pesos! Além disso, você pode sempre realizar uma experiência numérica e ver como os pesos da grade treinada se comportam de amostra em amostra. Vamos ver?
Para este fim, vamos realizar 500 experimentos que se deslocam por uma barra a cada vez e aprender a prever o próximo. Ensinaremos de novo a rede em cada bar. Para evitar a exibição do vetor de pesos todas as 500 vezes em um gráfico, obteremos valores médios para cada peso e os mostraremos mostrando a variância (dispersão de valores) correspondente a cada peso na forma do cabo traçado ao longo do nível 1/e:
O eixo de abcissas mostra o número da entrada NS, o eixo de ordenadas o valor médio do peso sobre esta entrada, para uma rede totalmente treinada. Como pode ser visto, para os marcadores de hora (fig. à esquerda), os valores dos pesos estão na área de sua dispersão estatística (alcance dos bigodes), o que refuta diretamente a hipótese de estacionaridade. O caso é um pouco melhor nos minutos; estatisticamente significativo é a primeira entrada de NS (amostra zero no gráfico) que é responsável pela conhecida antipessoalidade do kotier (coeficiente de correlação negativa em uma série da primeira diferença entre amostras vizinhas) em pequenas TFs.
Assim, é prematuro falar sobre a necessidade de desenvolver um método para aproximar os pesos NS por um polinômio.