Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Não, não é isso. De acordo com esta fórmula, parece que a GVH está correlacionada. Todo o tempo r é cerca de 0,5 menos.
Aqui está o código de teste.
Verifiquei.
Sergei, vamos dar um passo de cada vez.
1. Trabalhamos com uma BP semelhante a uma citação. Tal série é obtida pela integração de CB com MO zero. Exemplo de CB com MO zero:
dX=rnorm(n+1,0,10), onde n+1 é o número de membros do CB com distribuição gaussiana, 0 é MO igual a zero no meu caso e 10 no seu exemplo, 10 é a largura desta distribuição no meu caso e 100 no seu. Para construir a BP semelhante ao preço, precisamos integrar a série inicial (encontrar sua soma comutativa):
Aqui está como é a distribuição dos incrementos do CB integrado (Fig. à esquerda) e os próprios incrementos no fundo da BP (linhas vermelhas e azuis na Fig. direita):
Sergey, estamos estudando as propriedades da BP (a azul), enquanto em seu posto, você substituiu a primeira diferença (dX na minha notação e X na sua) na fórmula para calcular o coeficiente de correlação da primeira diferença da série. É claro, você receberá R=0,5 e não deve haver outro (é comprovadamente elementar). Portanto, se agora você calcular pela minha proposta de fórmula r para CB integrado com zero MO (o azul na figura certa), você receberá o zero esperado:
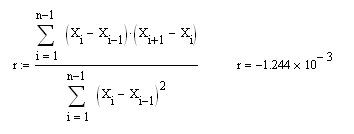
E, claro, isto é o mesmo que r para uma série de incrementos dX (mas, por uma fórmula diferente):
Espero que agora tenhamos um consenso sobre este ponto.
P.S. Você poderia fazer desta maneira:
Muito bem, vamos deixar isso claro.
Eu fiz o que você disse, reintegrei o CB com MOJ=0. Aqui está todo o código.
Parece estar tudo bem à primeira vista. Mas há uma armadilha. Vamos alimentar uma matriz correlacionada com a entrada da fórmula. Como tendência + ruído. y=a*x+b+rnorm(). Isto pode ser feito simplesmente ajustando 0,5 em vez de MOJ=0.
Pela figura você pode ver que a curva (azul) está claramente correlacionada. Tendo-o dividido em duas matrizes A e B, vamos calcular o coeficiente de correlação, ele acaba sendo de 0,993. De acordo com sua fórmula, é 0,225.
A questão é que, por definição, o coeficiente de correlação (CC) é contado entre as duas matrizes. Você está usando o mesmo. Você pode fazer isso comparando uma matriz a si mesmo. Chama-se ACF, ou seja, formam-se duas matrizes A - inicial, e a segunda B deslocada no tempo em relação a A, e constrói-se um gráfico - a dependência do coeficiente de correlação em relação ao turno. Se não houver turno, a ACF, é claro, = 1. Aqui está a trama ACF da última curva azul.
Esta é a aproximação. Portanto, continuo fiel à minha opinião de que você está calculando por esta fórmula, mas ela não é AC. Os números não batem certo.
Mas nós fomos para o lado. Primeiro devemos calcular o Hurst corretamente e depois ver como ele difere do CQ.
Aqui está um trabalho interessante que analisa diferentes séries cronológicas
usando o índice Hearst.
A figura mostra que a curva (azul) está claramente correlacionada. Dividindo-o em duas matrizes A e B, encontramos o coeficiente de correlação, que é de 0,993. Sua fórmula nos dá 0,225.
Aqui eu não entendo completamente.
Em quais matrizes você dividiu a tendência BP? Em um Y=a*X+b reto e um componente aleatório com MO zero, e entre eles você procura o coeficiente de correlação?
Aqui está um artigo interessante que faz uma análise de várias séries cronológicas
usando o índice Hearst.
Eu não consegui tudo aqui.
Agora eu entendo.
Você está procurando o coeficiente de correlação entre a BP original (não seus incrementos) e a mesma BP, mas deslocada por 500 contagens para a direita. Ou seja, você está procurando o coeficiente de correlação entre duas BPs sempre positivas! Bem, é claro que será sempre positivo e muito grande (cerca de 1).
Sergey, eu não o entendo! O que você conta, o coeficiente de correlação entre a BP inicial e a mesma, mas deslocada? Para que diabos nós precisamos disso! Estamos interessados no coeficiente de correlação entre as amostras vizinhas na série da primeira diferença da BP inicial. É este coeficiente que mostra a dependência do incremento esperado em relação aos incrementos anteriores. É este coeficiente que é idêntico ao de Hurst deslocado por 1/2.
>> Obrigado. >> Veremos.
Parece haveraqui alguma verdade.
Tentei implementá-la, mas cheguei muito perto de 1 para tarifas.
______________
Reler o artigo -- acho que estou no lado errado da moeda.
Para os pares de moedas, o índice Hearst deve ser calculado para o derivativo, eu o calculei para a taxa de câmbio.
Reler o artigo -- uma espécie de ancinho pisado.
Sim:-)
Me antecipar a mim mesmo.
Aqui está como fica a série da taxa integrada SV e EURGBP (Fig. à esquerda), e aqui está como são plotadas as amplitudes de seus incrementos em diferentes TFs em dupla escala logarítmica (Fig. à direita), no eixo de abcissas o logaritmo do TF:
Ela afirma que a tangente do ângulo de inclinação dessas linhas é igual a 1/2 para uma variável aleatória integrada (não faz sentido comercializar em tal quociente), menos de 1/2 para um mercado pullback e maior que 1/2 para um mercado trend. Vamos ver o que este ângulo é igual para NE. Aqui podemos, como aconselhado no artigo, traçar uma linha ISC e encontrar sua inclinação, mas encontrarei este valor localmente - traçando uma linha a cada dois pontos. O resultado será um PC para cada TF:
Os círculos aqui mostram o PC para o CB (vermelho) e azul para o quociente EURGBP no eixo de abcissas para o TF em min. As cruzes mostram o coeficiente de correlação entre as leituras vizinhas para a primeira diferença da série original com um offset de 1/2. O coeficiente de correlação foi calculado de acordo com a fórmula dada na primeira mensagem desta página. Pode-se ver que o acordo entre estas duas formas de estimar a previsibilidade da BP é satisfatório, enquanto as fórmulas no meu caso são muito menores (apenas uma). O que, de fato, é o que era necessário mostrar.
Além disso, a série Random deu PX=1/2 e r=0 (há um viés na figura), como segue a partir da definição. Para o quociente, é claramente visível uma tendência de rolamento (antipessoalidade), quanto maior, menor a TF.
Aqui mostramos PCB para CB (vermelho) e em azul para EURGBP kotier no eixo de abcissas o TF é plotado em min.
A série aleatória deu PX=1/2 e r=0 (há um viés na figura) como segue a partir da definição. Para o cotier, podemos ver claramente uma tendência de retrocesso (antipessoal), quanto maior, menor a TF.
É provavelmente por isso que os pips são tão afeiçoados à libra esterlina
Acho que é por isso que os encanadores gostam tanto da libra euro.
É óbvio!
É óbvio!
Por pura curiosidade - eu gostaria de encontrar pares extremamente persistentes,
ou pelo menos as condições sob as quais a persistência ocorre):