joo
Para começar, penso que é preciso levar o código:
1. Compilável.
2. Forma legível.
3. Comentário.
Ok.
Temos um conjunto ordenado de números reais. É necessário escolher uma célula na matriz com uma probabilidade correspondente ao tamanho do sector da roleta imaginária.
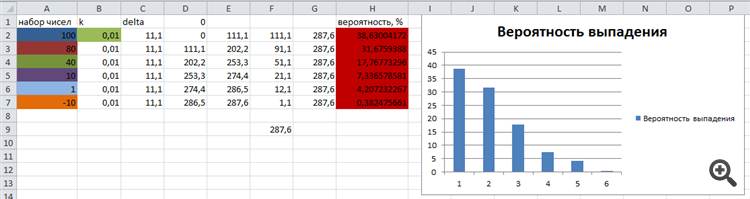
O conjunto de números de teste e a sua probabilidade teórica de queda são calculados em Excel e apresentados para comparação com os resultados do algoritmo na figura seguinte:
O resultado da execução do algoritmo:
2012.04.04 21:35:12 Roleta (EURUSD,H1) h0 38618465 38.618465
2012.04.04 21:35:12 Roleta (EURUSD,H1) h1 31685360 31.68536
2012.04.04 21:35:12 Roleta (EURUSD,H1) h3 7.334754 7.334754
2012.04.04 21:35:12 Roleta (EURUSD,H1) h4 4205492 4.205492
2012.04.04 21:35:12 Roleta (EURUSD,H1) h5 385095 0.385095
2012.04.04 21:35:12 Roleta (EURUSD,H1) 12028 ms - Tempo de execução
Como se pode ver, os resultados da probabilidade da "bola" cair sobre o sector correspondente são quase idênticos aos teóricos calculados.
#property script_show_inputs //--- input parameters input int StartCount=100000000; // Границы соответствующих секторов рулетки double select1[]; // начало сектора double select2[]; // конец сектора //—————————————————————————————————————————————————————————————————————————————— void OnStart() { MathSrand((int)TimeLocal());// сброс генератора // массив с тестовым набором чисел double array[6]={100.0,80.0,40.0,10.0,1.0,-10.0}; ArrayResize(select1,6);ArrayInitialize(select1,0.0); ArrayResize(select2,6);ArrayInitialize(select2,0.0); // счетчики для подсчета выпадений соответствующего числа из тестового набора int h0=0,h1=0,h2=0,h3=0,h4=0,h5=0; // нажмём кнопочку секундомера int time_start=(int)GetTickCount(); // проведём серию испытаний for(int i=0;i<StartCount;i++) { switch(Roulette(array,6)) { case 0: h0++;break; case 1: h1++;break; case 2: h2++;break; case 3: h3++;break; case 4: h4++;break; default: h5++;break; } } Print((int)GetTickCount()-time_start," мс - Время исполнения"); Print("h5 ",h5, " ",h5*100.0/StartCount); Print("h4 ",h4, " ",h4*100.0/StartCount); Print("h3 ",h3, " ",h3*100.0/StartCount); Print("h1 ",h1, " ",h1*100.0/StartCount); Print("h0 ",h0, " ",h0*100.0/StartCount); Print("----------------"); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Рулетка. int Roulette(double &array[], int SizeOfPop) { int i=0,u=0; double p=0.0,start=0.0; double delta=(array[0]-array[SizeOfPop-1])*0.01-array[SizeOfPop-1]; //------------------------------------------------------------------------------ // зададим границы секторов for(i=0;i<SizeOfPop;i++) { select1[i]=start; select2[i]=start+MathAbs(array[i]+delta); start=select2[i]; } // бросим "шарик" p=RNDfromCI(select1[0],select2[SizeOfPop-1]); // посмотрим, на какой сектор упал "шарик" for(u=0;u<SizeOfPop;u++) if((select1[u]<=p && p<select2[u]) || p==select2[u]) break; //------------------------------------------------------------------------------ return(u); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Генератор случайных чисел из заданного интервала. double RNDfromCI(double min,double max) {return(min+((max-min)*MathRand()/32767.0));} //——————————————————————————————————————————————————————————————————————————————
OK.
Temos um conjunto ordenado de números reais. Precisamos de seleccionar uma célula na matriz com uma probabilidade correspondente ao tamanho do sector da roleta imaginária.
Explique o princípio da definição da "largura do sector". Corresponde aos valores da matriz? Ou é definido separadamente?
Esta é a questão mais sombria, o resto não é problema.
Segunda pergunta: Qual é o número 0,01? De onde veio?
Em resumo: Diga-me onde obter as probabilidades correctas de abandono do sector (largura como uma fracção da circunferência).
Pode apenas o tamanho de cada sector. Desde que (o padrão) não exista o tamanho negativo na natureza. Mesmo no casino. ;)
Explique o princípio da definição da "largura do sector". Corresponde aos valores da matriz? Ou é definido separadamente?
A largura dos sectores não pode corresponder aos valores da matriz, caso contrário o algoritmo não funcionará para todos os números.
O que importa é a distância que os números estão entre si. Quanto mais afastados estiverem todos os números do primeiro, menos provável é que caiam. Na essência adiamos numa linha recta barras proporcionais à distância entre os números, ajustadas por um factor de 0,01, de modo a que o último número a probabilidade de cair não fosse igual a 0 como o mais afastado do primeiro. Quanto mais elevado for o coeficiente, mais iguais são os sectores. Ficheiro Excel em anexo, experimente com ele.
MetaDriver:
1. Em resumo: Diga-me onde obter as probabilidades correctas de abandono do sector (largura em fracções da circunferência).
2. Pode apenas dimensionar cada sector. assumindo (por defeito) que não existem tamanhos negativos na natureza. nem mesmo em casinos. ;)1. O cálculo das probabilidades teóricas é dado em excel. O primeiro número é a probabilidade mais alta, o último número é a probabilidade mais baixa mas não é igual a 0.
2) As dimensões negativas dos sectores nunca existem para qualquer conjunto de números, desde que o conjunto seja classificado por ordem decrescente - o primeiro número é o maior (funcionará com o maior do conjunto mas com um número negativo).
A largura dos sectores não pode corresponder aos valores da matriz, caso contrário o algoritmo não funcionará para todos os números.
hu: O que importa é a distância a que os números estão separados. Quanto mais afastados estiverem todos os números do primeiro número, menor é a probabilidade de caírem. Em essência, adiamos num segmento de recta proporcional às distâncias entre os números, ajustado por um factor de 0,01, de modo a que a probabilidade do último número não cair fosse 0 como o mais afastado do primeiro. Quanto mais elevado for o coeficiente, mais iguais são os sectores. O ficheiro excel está anexado, experimente com ele.
1. O cálculo das probabilidades teóricas é dado no Excel. O primeiro número é a probabilidade mais alta, o último número é a probabilidade mais baixa mas não é igual a 0.
2. nunca haverá tamanhos negativos de sectores para qualquer conjunto de números, desde que o conjunto seja classificado por ordem decrescente - o primeiro número é o maior (funcionará com o maior do conjunto mas também com um número negativo).
O seu esquema "do nada" estabelece a probabilidade do menor número(vmh). Não há nenhuma justificação razoável.
// Uma vez que "justificação" é um pouco difícil. Não faz mal - só há lacunas N-1 entre os pregos N.
Portanto, depende do "coeficiente", também retirado da caixa. porquê 0,01 ? por que não 0,001 ?
Antes de fazer o algoritmo, é necessário decidir sobre o cálculo da "largura" de todos os sectores.
zyu: Dê a fórmula para calcular "distâncias entre números". Qual é o número "primeiro"? Que distância está de si mesmo? Não o envie para o Excel, eu já lá estive. É confuso a um nível ideológico. De onde vem o factor de correcção e porque é que é assim?
O de vermelho não é de todo verdade. :)
será muito rápido:
int Selection() { return(RNDfromCI(1,SizeOfPop); }
A qualidade do algoritmo como um todo não deve ser afectada.
E mesmo que o faça, esta opção irá ultrapassar a qualidade à custa da velocidade.
1. O seu esquema "do nada" estabelece a probabilidade do menor número(vmh). Não há nenhuma justificação razoável. Por isso(vmh) depende do "coeficiente" também "fora da caixa". porquê 0,01 ? por que não 0,001 ?
2. Antes de fazer o algoritmo, é necessário decidir sobre o cálculo da "largura" de todos os sectores.
3. zu: Dê a fórmula para calcular "distâncias entre números" . Qual é o número "primeiro"? A que distância está de si mesmo? Não o envie para o Excel, eu já lá estive. É confuso a um nível ideológico. De onde vem sequer o factor de correcção e porquê exactamente?
4. O sublinhado em vermelho não é de todo verdade. :)
1. Sim, não é verdade. Gosto deste coeficiente. Se gostar de outro, usarei outro - a velocidade do algoritmo não mudará.
2. A certeza é alcançada.
3. ok. temos uma ordenação de números - matriz[], onde o maior número está na matriz[0], e o raio de números com um ponto de partida 0.0 (pode tomar qualquer outro ponto - nada mudará) e dirigido na direcção positiva. Organizar os segmentos no raio desta forma:
start0=0=0 end0=start0+|array[0]+delta|
start1=end0 end1=start1+|array[1]+delta|
start2=end1 end2=start2+|array[2]+delta|
......
start5=end4 end5=start5+|array[5]+delta|
Onde:
delta=(array[0]-array[5])*0.01-array[5];
Isso é tudo a aritmética. :)
Agora, se lançarmos uma "bola" no nosso raio marcado, a probabilidade de atingirmos um determinado segmento é proporcional ao comprimento desse segmento.
4. Porque salientou o erro (não todos). Deve salientar:"Essencialmente, estamos a traçar na linha numérica os segmentos proporcionais às distâncias entre os números, corrigidos por um factor de 0,01 para que o último número não tenha uma probabilidade de atingir 0".
será muito rápido:
int Selection() { return(RNDfromCI(1,SizeOfPop); }
A qualidade do algoritmo como um todo não deve ser afectada.
E se mesmo ligeiramente afectado, irá ultrapassar a qualidade à custa da velocidade.
:)
Está a sugerir que se seleccione simplesmente um elemento da matriz ao acaso? - Isto não tem em conta as distâncias entre números de matriz, pelo que a sua opção é inútil.

- www.mql5.com
:)
Está a sugerir que simplesmente seleccione um elemento da matriz ao acaso? - Isso não tem em conta a distância entre os números da matriz, pelo que a sua opção não vale nada.
não é difícil de verificar.
Está confirmado experimentalmente que é inapropriado?
está confirmado experimentalmente que não vale nada?
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Sugiro discutir aqui problemas de lógica de algoritmo óptima.
Se alguém duvida que o seu algoritmo tem uma lógica óptima em termos de velocidade (ou clareza), então é bem-vindo.
Além disso, dou as boas-vindas a este fio àqueles que querem praticar os seus algoritmos e ajudar outros.
Originalmente coloquei a minha pergunta no ramo "Perguntas de um Dummie", mas apercebi-me, que o seu lugar não é lá.
Portanto, sugerimos uma variante mais rápida do algoritmo da "roleta" do que esta:
Claramente, as matrizes podem ser retiradas da função, pelo que não têm de ser declaradas sempre e redimensionadas, mas preciso de uma solução mais revolucionária. :)