워밍업과 시간이 걸리는 학교 문제 - 페이지 7 12345678 새 코멘트 Aleksey Nikolayev 2020.09.27 17:28 #61 Nikolai Semko : 그렇습니까? 이제 컴퓨터가 아닙니다. 내가 시도한 것처럼. ME는 이 기능을 인식하지 못했고 F1 도움말에서 찾지 못했습니다. 나는 이것이 AlgLib 라이브러리라는 것을 이해합니다. https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum Vladimir Simakov 2020.09.27 18:06 #62 Aleksey Nikolayev : https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum 음디아. 구현... 이것은 Liba입니다. 다음과 같아야 합니다. 1. null 배열을 사용하여 기본 생성자에 의해 초기화된 값을 반환합니다(프리미티브의 경우 0). template < typename T> T MathSum( const T &arr[]){ T sum=T(); for ( int i= 0 ,size= ArraySize (arr);i<size;sum+=arr[i++]); return sum; } 2. 배열이 0이면 런타임에 충돌이 발생합니다. template < typename T> T MathSum( const T &arr[]){ T sum=arr[ 0 ]; for ( int i= 1 ,size= ArraySize (arr);i<size;sum+=arr[i++]); return sum; } 3. 작업 결과의 코드와 금액을 포함하는 구조를 반환합니다. template < typename T> struct SRet{ int retCode; //0 - Ок, -1 - Not initialized T res; SRet():retCode(- 1 ){} SRet( uint code, const T &_res):retCode(code),res(_res){} SRet(const SRet<T> &other) {this=other;} bool operator !() const { return retCode!= 0 ;} }; template < typename T> SRet<T> MathSum( const T &arr[]){ int size= ArraySize (arr); if (!size) return SRet<T>(); SRet<T> ret(0,arr[ 0 ]); for ( int i= 1 ,size= ArraySize (arr);i<size;ret.res+=arr[i++]); return ret; } 무엇이라고 불리는지, 무엇을 더 좋아합니까?))) 그는 무릎을 꿇고 글을 썼습니다. 그래서 어딘가에 잼을 망칠 수있었습니다. Andrei Trukhanovich 2020.09.27 18:25 #63 Aleksey Nikolayev : Cramer의 정리에 대한 정보는 이 책 에 있습니다(부록, 102페이지). 감사하다! (단단한) 원 정리를 통해 증명하기가 매우 쉽습니다. Aleksey Nikolayev 2020.09.27 18:26 #64 Vladimir Simakov : 음디아. 구현... 이것은 Liba입니다. 다음과 같아야 합니다. 1. null 배열을 사용하여 기본 생성자에 의해 초기화된 값을 반환합니다(프리미티브의 경우 0). 2. 배열이 0이면 런타임에 충돌이 발생합니다. 3. 작업 결과의 코드와 금액을 포함하는 구조를 반환합니다. 무엇이라고 불리는지, 무엇을 더 좋아합니까?))) 그는 무릎을 꿇고 글을 썼습니다. 그래서 어딘가에 잼을 망칠 수있었습니다. 글쎄, 그것은 쓰여졌다: "우리는 R에서 하는 것처럼, 다만 더 빠를 뿐입니다." C ++에서 약속되지 않았기 때문입니다. Vladimir Simakov 2020.09.27 18:38 #65 Aleksey Nikolayev : 글쎄, 그것은 쓰여졌다: "우리는 R에서 하는 것처럼, 단지 더 빠를 뿐입니다." C ++에서 약속되지 않았기 때문입니다. 약한 변명. R에서 좋아하세요... 모르겠습니다. R은 내 스택에 없습니다. 즉, C++로 라이브러리를 작성할 때 템플릿을 사용하지 않는 것입니다(C++처럼 보이고 C++ 냄새가 나며 UB가 있어도 ...) - 이것은 어떻게 든 ... Nikolai Semko 2020.09.27 18:44 #66 Aleksey Nikolayev : https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum 도움말에 있지만 컴파일러에는 표시되지 않습니다. 저만 그런가요? 추신 방금 당신이 가지고있는 것을 보았습니다 #include <Math\Stat\Math.mqh> 모두 동일한 외부 성경을 의미합니다. 다시 한 번, 나는 한 줄의 코드를 저장하기 위해 내 프로그램에 추가 라이브러리를 추가할 요점을 알지 못합니다. Maxim Kuznetsov 2020.09.27 19:25 #67 Nikolai Semko : 다시 한 번, 나는 한 줄의 코드를 저장하기 위해 내 프로그램에 추가 라이브러리를 추가할 요점을 알지 못합니다. 특정 경우에 대한 프로그램은 -입니다. MathSum에 대한 소문은 관련이 없습니다. 더 중요한 문제를 배경으로: 우리는 이 솔루션이 외접 원의 중심이 그림 내부에 있는 경우에만 작동한다는 것을 위에서 알았습니다. 즉, 적용 가능성의 또 다른 기준이 필요합니다. "여기에 - 결과가 유감이지만 그러한 노-shmogo에 대해" 이제 주제는 최적화 프로그램에 의한 최적화와 직접 관련이 있습니다 ... Aleksey Nikolayev 2020.09.27 19:53 #68 Maxim Kuznetsov : 특정 경우에 대한 프로그램은 -입니다. MathSum에 대한 소문은 관련이 없습니다. 더 중요한 문제를 배경으로: 우리는 이 솔루션이 외접 원의 중심이 그림 내부에 있는 경우에만 작동한다는 것을 위에서 알았습니다. 즉, 적용 가능성의 또 다른 기준이 필요합니다. "이를 위해 - 결과가 유감이지만 그러한 노 shmogo에 대해" 이제 주제는 최적화 프로그램에 의한 최적화와 직접적인 관련이 있습니다. 언뜻 보면 R을 결정하는 방정식만 변경됩니다. 1) 센터 내부의 경우: A1+A2+...+An=2*Pi 2) 중앙 바깥쪽의 경우: A1-A2-...-An=0, 여기서 A1은 가장 긴 변의 각도입니다. 따라서 이 두 경우를 구별하는 방법만 결정하면 됩니다. 추신. 일반적으로 반지름이 최대 변의 절반인 경우 각 Ai의 합을 계산해야 합니다. 2 * Pi보다 작으면 중심이 다각형 외부에 있고 그 반대의 경우도 마찬가지입니다. Nikolai Semko 2020.09.27 22:12 #69 Maxim Kuznetsov : 특정 경우에 대한 프로그램은 -입니다. MathSum에 대한 소문은 관련이 없습니다. 더 중요한 문제를 배경으로: 우리는 이 솔루션이 외접 원의 중심이 그림 내부에 있는 경우에만 작동한다는 것을 위에서 알았습니다. 즉, 적용 가능성의 또 다른 기준이 필요합니다. "여기에 - 결과가 유감이지만 그러한 노-shmogo에 대해" 이제 주제는 최적화 프로그램에 의한 최적화와 직접 관련이 있습니다 ... 글쎄, 왜 나는 할 수 없습니다. 당신은 시간을 보낼 필요가 있지만 무엇을 위해 - 그것은 분명하지 않습니다. Simakov가 이미 그랬던 것처럼. 사실, 나는 이해하지 못했습니다. 좋아, 내 방식대로 해볼게. 모든 것을 시각적으로 보기 위해. Nikolai Semko 2020.09.27 23:30 #70 파일: Zadacha3.mq5 9 kb 12345678 새 코멘트 트레이딩 기회를 놓치고 있어요: 무료 트레이딩 앱 복사용 8,000 이상의 시그널 금융 시장 개척을 위한 경제 뉴스 등록 로그인 공백없는 라틴 문자 비밀번호가 이 이메일로 전송될 것입니다 오류 발생됨 Google으로 로그인 웹사이트 정책 및 이용약관에 동의합니다. 계정이 없으시면, 가입하십시오 MQL5.com 웹사이트에 로그인을 하기 위해 쿠키를 허용하십시오. 브라우저에서 필요한 설정을 활성화하시지 않으면, 로그인할 수 없습니다. 사용자명/비밀번호를 잊으셨습니까? Google으로 로그인
그렇습니까?
https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum
https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum
음디아. 구현...
이것은 Liba입니다. 다음과 같아야 합니다.
1. null 배열을 사용하여 기본 생성자에 의해 초기화된 값을 반환합니다(프리미티브의 경우 0).
2. 배열이 0이면 런타임에 충돌이 발생합니다.
3. 작업 결과의 코드와 금액을 포함하는 구조를 반환합니다.
무엇이라고 불리는지, 무엇을 더 좋아합니까?)))
그는 무릎을 꿇고 글을 썼습니다. 그래서 어딘가에 잼을 망칠 수있었습니다.
Cramer의 정리에 대한 정보는 이 책 에 있습니다(부록, 102페이지).
감사하다! (단단한) 원 정리를 통해 증명하기가 매우 쉽습니다.
음디아. 구현...
이것은 Liba입니다. 다음과 같아야 합니다.
1. null 배열을 사용하여 기본 생성자에 의해 초기화된 값을 반환합니다(프리미티브의 경우 0).
2. 배열이 0이면 런타임에 충돌이 발생합니다.
3. 작업 결과의 코드와 금액을 포함하는 구조를 반환합니다.
무엇이라고 불리는지, 무엇을 더 좋아합니까?)))
그는 무릎을 꿇고 글을 썼습니다. 그래서 어딘가에 잼을 망칠 수있었습니다.
글쎄, 그것은 쓰여졌다: "우리는 R에서 하는 것처럼, 다만 더 빠를 뿐입니다." C ++에서 약속되지 않았기 때문입니다.
글쎄, 그것은 쓰여졌다: "우리는 R에서 하는 것처럼, 단지 더 빠를 뿐입니다." C ++에서 약속되지 않았기 때문입니다.
약한 변명.
R에서 좋아하세요... 모르겠습니다. R은 내 스택에 없습니다.
즉, C++로 라이브러리를 작성할 때 템플릿을 사용하지 않는 것입니다(C++처럼 보이고 C++ 냄새가 나며 UB가 있어도 ...) - 이것은 어떻게 든 ...
https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum
도움말에 있지만 컴파일러에는 표시되지 않습니다.
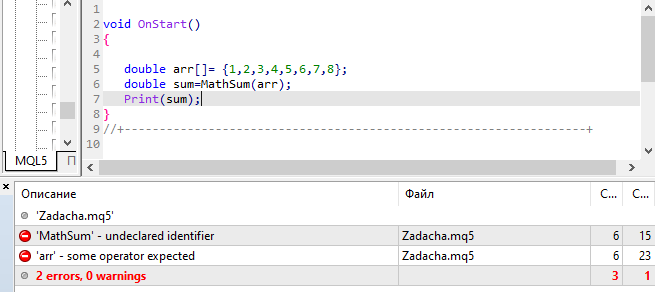
저만 그런가요?
추신 방금 당신이 가지고있는 것을 보았습니다
#include <Math\Stat\Math.mqh>모두 동일한 외부 성경을 의미합니다.
다시 한 번, 나는 한 줄의 코드를 저장하기 위해 내 프로그램에 추가 라이브러리를 추가할 요점을 알지 못합니다.
다시 한 번, 나는 한 줄의 코드를 저장하기 위해 내 프로그램에 추가 라이브러리를 추가할 요점을 알지 못합니다.
특정 경우에 대한 프로그램은 -입니다. MathSum에 대한 소문은 관련이 없습니다.
더 중요한 문제를 배경으로: 우리는 이 솔루션이 외접 원의 중심이 그림 내부에 있는 경우에만 작동한다는 것을 위에서 알았습니다.
즉, 적용 가능성의 또 다른 기준이 필요합니다. "여기에 - 결과가 유감이지만 그러한 노-shmogo에 대해"
이제 주제는 최적화 프로그램에 의한 최적화와 직접 관련이 있습니다 ...
특정 경우에 대한 프로그램은 -입니다. MathSum에 대한 소문은 관련이 없습니다.
더 중요한 문제를 배경으로: 우리는 이 솔루션이 외접 원의 중심이 그림 내부에 있는 경우에만 작동한다는 것을 위에서 알았습니다.
즉, 적용 가능성의 또 다른 기준이 필요합니다. "이를 위해 - 결과가 유감이지만 그러한 노 shmogo에 대해"
이제 주제는 최적화 프로그램에 의한 최적화와 직접적인 관련이 있습니다.
언뜻 보면 R을 결정하는 방정식만 변경됩니다.
1) 센터 내부의 경우: A1+A2+...+An=2*Pi
2) 중앙 바깥쪽의 경우: A1-A2-...-An=0, 여기서 A1은 가장 긴 변의 각도입니다.
따라서 이 두 경우를 구별하는 방법만 결정하면 됩니다.
추신. 일반적으로 반지름이 최대 변의 절반인 경우 각 Ai의 합을 계산해야 합니다. 2 * Pi보다 작으면 중심이 다각형 외부에 있고 그 반대의 경우도 마찬가지입니다.
특정 경우에 대한 프로그램은 -입니다. MathSum에 대한 소문은 관련이 없습니다.
더 중요한 문제를 배경으로: 우리는 이 솔루션이 외접 원의 중심이 그림 내부에 있는 경우에만 작동한다는 것을 위에서 알았습니다.
즉, 적용 가능성의 또 다른 기준이 필요합니다. "여기에 - 결과가 유감이지만 그러한 노-shmogo에 대해"
이제 주제는 최적화 프로그램에 의한 최적화와 직접 관련이 있습니다 ...
글쎄, 왜 나는 할 수 없습니다.
당신은 시간을 보낼 필요가 있지만 무엇을 위해 - 그것은 분명하지 않습니다.
Simakov가 이미 그랬던 것처럼. 사실, 나는 이해하지 못했습니다.
좋아, 내 방식대로 해볼게. 모든 것을 시각적으로 보기 위해.