[아카이브] 순수수학, 물리학, 화학 등 : 거래와 무관한 두뇌 트레이닝 퍼즐 - 페이지 614 1...607608609610611612613614615616617618619620621...628 새 코멘트 [삭제] 2012.07.04 12:45 #6131 Mathemat : Dima , 1000분의 1 퍼센트와 다른 확률을 왜 알아야 합니까? 보장을 원하면 아무 것도 없습니다. 노벨상 수상자(LTCM)와 Niederhofer 자신은 11도 이하의 확률로 스스로를 덮었지만 여전히 "적중"했습니다. 1/1000 퍼센트 - 필요하지 않습니다. 그러나 120 거래는 많은 거래입니다. 예를 들어 20, 30, 40과 같이 적은 수의 거래에 대해 계산할 수 있어야 합니다. 그리고 30%는 120에 충분하지 않습니다. 그리고 매우 작은 확률(매우 큰)은 시스템의 대략적인 수명을 계산하는 데 사용됩니다. 그것이 얼마나 오래 작동할 것인지 아는 것이 중요합니다. 1년 또는 10년입니다. 의지할 것이 있습니까? 수학의 경우 그게 전부입니다. 10포인트 3.mq4 포럼을 어지럽히 지 않도록 거래량, 변동성 및 허스트 Sceptic Philozoff 2012.07.04 13:05 #6132 글쎄, 적어도 terver에서 이니셜을 읽으면 여전히 유용할 것입니다. [삭제] 2012.07.04 13:08 #6133 GaryKa, Mathemat 그래서? Sceptic Philozoff 2012.07.04 13:23 #6134 DmitriyN : 그래서? 정확히! 그러나 반올림 오류는 모든 정밀도를 갉아먹을 수 있습니다. 0에서 30까지 합계를 계산하는 것이 좋습니다. 알고자 하는 확률을 더한 값과 같습니다. GaryKa 2012.07.04 13:27 #6135 공이 반환되면 항상 p=q이므로 우변의 공식을 단순화할 수 있습니다(* p^120) Sceptic Philozoff 2012.07.04 13:29 #6136 Mislaid : 우리는 문제를 근본적으로 해결합니다. 즉, 평등이 없습니다. 우리는 정육면체의 면에 있는 숫자 집합이 교차하지 않아야 한다고 결정합니다. 더 많이 먹습니다. 면의 합이 17인 경우가 있습니다. 예를 들어 (333332) > (662111), 그리고 당첨 확률은 23/36 ~ 0.64입니다. 사실, 모든 것이 간단하지 않습니다. (662111) 눈에 띄는 이점이 있는 사람을 상대로 이기지 못합니다. 면의 합이 18인 반면 가장 비옥한 것 같습니다. Sceptic Philozoff 2012.07.04 13:47 #6137 GaryKa : 공이 반환되면 항상 p=q이므로 우변의 공식을 단순화할 수 있습니다(* p^120) 우리가 돌아오든 말든 그것은 중요하지 않습니다. 영향을 미치기에는 너무 적게 추출합니다. 하지만 훨씬 쉽게 만들 수 있습니다. 그리고 인수 (1/2) ^ 120은 거듭제곱이 있는 괄호 안에 남아 있습니다. 헤헤. 2 Dima : 이 조합으로 어지럽힐 일이 없습니다. 정규 분포를 처리하고 0에서 30에 해당하는 하한까지 명확한 적분을 취하십시오. 이 공식의 조합을 사용하면 조합의 단순 합계에 대한 분석 공식을 찾지 못하면 실수를 하게 됩니다. 또는 0에서 30까지 조합의 합을 계산하려고 시도하면 p도가 방해하지 않습니다. 갑자기 운이 좋았습니다. 추신 요컨대, 모든 것이 간단합니다. 여기 봐 . k1, k2를 계산한 다음 적분을 계산해야 합니다. k1=0, k2=30을 취하므로 더 정확합니다. n=120, p=q=1/2. 그 다음에 (k2-np)/sqrt(npq) = (30-60)/sqrt(120*1/2*1/2) ~ -5.477 (k1-np)/sqrt(npq) = (0-60)/sqrt(120*1/2*1/2) ~ -10.954. 여전히 유용한 것은 1/sqrt(2*pi) ~ 0.39894입니다. 적분 한계 내에서 처음 두 숫자를 대체하고 0.39894*exp(-x^2/2)를 피적분 함수에 대입하고 다음을 얻습니다( 여기 에 특정 적분을 취하는 서비스가 있습니다). 2.163*10^(-8). 따라서 확률은 1-2.163*10^(-8) ~ 0.99999998입니다. 적분 아래에서 함수의 역도함수를 취하려고 하지도 마십시오. 이것은 기본적이지 않습니다. [Archive!] Pure mathematics, physics, 확률적 공명 푸리에 감정가 .. GaryKa 2012.07.04 14:22 #6138 Mathemat : ... 정규 분포를 다루십시오 ... 단순 조합의 합에 대한 분석 공식을 찾을 수 없다면 ... 당신의이 단어는 흥미로운 생각을 일으켰습니다-정규 분포를 통해 조합을 계산하는 분석 공식을 찾으십시오)) [삭제] 2012.07.04 14:25 #6139 Mathemat : 나는 그것을 알아 내려고 노력할 것입니다. 좋은 링크. Sceptic Philozoff 2012.07.04 14:41 #6140 GaryKa : 당신의이 단어는 흥미로운 생각을 일으켰습니다 - 정규 분포를 통해 조합을 계산하는 분석 공식을 찾으십시오)) 이것은 지역 Moivre-Laplace 정리 입니다. 1...607608609610611612613614615616617618619620621...628 새 코멘트 트레이딩 기회를 놓치고 있어요: 무료 트레이딩 앱 복사용 8,000 이상의 시그널 금융 시장 개척을 위한 경제 뉴스 등록 로그인 공백없는 라틴 문자 비밀번호가 이 이메일로 전송될 것입니다 오류 발생됨 Google으로 로그인 웹사이트 정책 및 이용약관에 동의합니다. 계정이 없으시면, 가입하십시오 MQL5.com 웹사이트에 로그인을 하기 위해 쿠키를 허용하십시오. 브라우저에서 필요한 설정을 활성화하시지 않으면, 로그인할 수 없습니다. 사용자명/비밀번호를 잊으셨습니까? Google으로 로그인
Dima , 1000분의 1 퍼센트와 다른 확률을 왜 알아야 합니까? 보장을 원하면 아무 것도 없습니다. 노벨상 수상자(LTCM)와 Niederhofer 자신은 11도 이하의 확률로 스스로를 덮었지만 여전히 "적중"했습니다.
그리고 매우 작은 확률(매우 큰)은 시스템의 대략적인 수명을 계산하는 데 사용됩니다. 그것이 얼마나 오래 작동할 것인지 아는 것이 중요합니다. 1년 또는 10년입니다.
의지할 것이 있습니까? 수학의 경우 그게 전부입니다.
그래서?
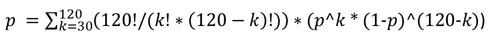
정확히!
그러나 반올림 오류는 모든 정밀도를 갉아먹을 수 있습니다. 0에서 30까지 합계를 계산하는 것이 좋습니다. 알고자 하는 확률을 더한 값과 같습니다.
면의 합이 17인 경우가 있습니다.
예를 들어 (333332) > (662111), 그리고 당첨 확률은 23/36 ~ 0.64입니다. 사실, 모든 것이 간단하지 않습니다. (662111) 눈에 띄는 이점이 있는 사람을 상대로 이기지 못합니다.
면의 합이 18인 반면 가장 비옥한 것 같습니다.
공이 반환되면 항상 p=q이므로 우변의 공식을 단순화할 수 있습니다(* p^120)
우리가 돌아오든 말든 그것은 중요하지 않습니다. 영향을 미치기에는 너무 적게 추출합니다. 하지만 훨씬 쉽게 만들 수 있습니다. 그리고 인수 (1/2) ^ 120은 거듭제곱이 있는 괄호 안에 남아 있습니다.
헤헤.
2 Dima : 이 조합으로 어지럽힐 일이 없습니다. 정규 분포를 처리하고 0에서 30에 해당하는 하한까지 명확한 적분을 취하십시오. 이 공식의 조합을 사용하면 조합의 단순 합계에 대한 분석 공식을 찾지 못하면 실수를 하게 됩니다.
또는 0에서 30까지 조합의 합을 계산하려고 시도하면 p도가 방해하지 않습니다. 갑자기 운이 좋았습니다.
추신 요컨대, 모든 것이 간단합니다. 여기 봐 .
k1, k2를 계산한 다음 적분을 계산해야 합니다.
k1=0, k2=30을 취하므로 더 정확합니다. n=120, p=q=1/2. 그 다음에
(k2-np)/sqrt(npq) = (30-60)/sqrt(120*1/2*1/2) ~ -5.477
(k1-np)/sqrt(npq) = (0-60)/sqrt(120*1/2*1/2) ~ -10.954.
여전히 유용한 것은 1/sqrt(2*pi) ~ 0.39894입니다.
적분 한계 내에서 처음 두 숫자를 대체하고 0.39894*exp(-x^2/2)를 피적분 함수에 대입하고 다음을 얻습니다( 여기 에 특정 적분을 취하는 서비스가 있습니다).
2.163*10^(-8).
따라서 확률은 1-2.163*10^(-8) ~ 0.99999998입니다.
적분 아래에서 함수의 역도함수를 취하려고 하지도 마십시오. 이것은 기본적이지 않습니다.