- Problem statement
- File arrangement structure
- Choosing the input data
- Creating the framework for the future MQL5 program
- Description of a Python script structure
- Fully connected neural layer
- Organizing parallel computing using OpenCL
- Implementing the perceptron model in Python
- Creating training and testing samples
- Gradient distribution verification
- Comparative testing of implementations
Gradient distribution verification
Now is the moment when we will assemble the first neural network using MQL5. However, I won't raise your hopes too much as our first neural network will not analyze or predict anything. Instead, it will perform a control function and verify the correctness of the work done earlier. The reason is that before we proceed directly to training the neural network, we need to check the correctness of the error gradient distribution throughout the neural network. I believe it is clear that the correctness of implementing this process significantly affects the overall result of the neural network training. After all, it is the error gradient on each weight that determines the magnitude and direction of its change.
To verify the correctness of gradient distribution, we can use the fact that there are two options to determine the derivative of a function:
- Analytical: determining the gradient of a function based on its first-order derivative. This method is implemented in our backward pass method.
- Empirical: under other equal conditions, the value of one indicator is changed and its effect on the final result of the function is evaluated.
In its geometric interpretation, the gradient is the slope of the tangent to the graph of the function at the current point. It indicates how the value of the function changes with a change in the parameter value.
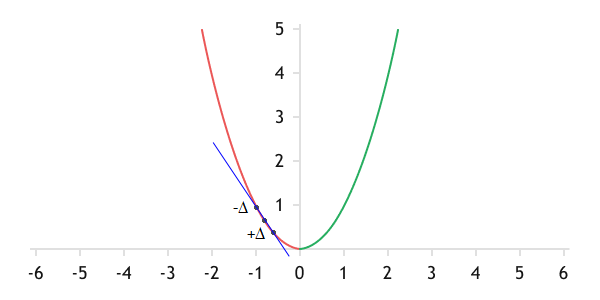
In geometry terms, the gradient is the slope of the tangent to the graph of the function at the current point
To draw a line, we need two points. Therefore, in two simple iterations, we can find these points on the graph of the function. First, we need to add a small number to the current value of the parameter and calculate the value of the function without changing the other parameters. This will be the first point. We repeat the iteration, but this time we subtract the same number from the current value and get the second point. The line passing through these two points will approximate the desired tangent with a certain degree of error. The smaller the number used to change the parameter, the smaller this error will be. This is the basis of the empirical method for determining the gradient.
If this method is so simple, why not use it consistently? Everything is quite simple here. The method simplicity hides a large number of operations:
- Perform a forward pass and save its result.
- Slightly increase one parameter and repeat the forward pass with the result saved.
- Slightly decrease one parameter and repeat the forward pass with the result saved.
- Based on the found points, construct a line and determine its slope.
All these steps are performed to determine the gradient at only one step for one parameter. Imagine how much time and computational resources we would need if we used this method in training a neural network with even just a hundred parameters. Do not forget that modern neural networks contain significantly more parameters. For instance, a giant model like GPT-3 contains 175 billion parameters. Of course, we will not build such giants on a home computer. However, the use of the analytical method greatly reduces the number of necessary iterations and the time for their execution.
At the same time, we can build a small neural network and compare the results of the two methods on it. Their similarity will indicate the correctness of the implemented analytical method algorithm. Significant discrepancies in the results of the two methods will indicate the need to reevaluate the backward pass algorithm implemented in the analytical method.
To implement this idea in practice, let's create the script check_gradient_percp.mq5. This script will receive three external parameters:
- the size of the initial data vector,
- flag for using OpenCL technology,
- function to activate the hidden layer.
Please note that we haven't specified the source of the original data. The reason is that for this work, it doesn't matter at all what data will be input into the model. We only check the correctness of the backward pass methods. Therefore, we can use a vector of random values as initial data.
//+------------------------------------------------------------------+
|
In addition, in the global scope of the script, we will connect our library and declare a neural network object.
//+------------------------------------------------------------------+
|
At the beginning of the script body, let's define the architecture of a small neural network. However, since we will need to perform similar tasks multiple times to validate the correctness of the process in different architectural solutions, we will encapsulate the model creation in a separate procedure called CreateNet. In the parameters, this procedure receives a pointer to the object of the neural network model being created.
Let me remind you that earlier we created the CNet::Create method to create a neural network model. In parameters, this method takes a dynamic array of descriptions of the neural network architecture. Therefore, we need to organize a similar description of the new model. Let's collect the description of each neural layer into a separate instance of the CLayerDescription class. We will combine them into a dynamic array CArrayObj. When adding neuron descriptions to a dynamic array, make sure that their sequence strictly corresponds to the arrangement of neural layers in the neural network. In my practice, I simply create layer descriptions sequentially in the order of their arrangement in the neural network and add them to the array as I create them.
bool CreateNet(CNet &net)
|
To check the correctness of the implemented error propagation algorithm, we will create a three-layer neural network. All layers will be built on the basis of the CNeuronBase class we created. The size of the first neural layer of the initial data was specified by the user in the external parameter BarsToLine. We will create it without an activation function and weight update method. In theory, this is the basic approach to creating a source data layer.
//--- source data layer
|
We will set the number of neurons in the second (hidden) neural layer to be 10 times greater than the input data layer. However, the actual size of the neural layer does not directly affect the process of analyzing the algorithm performance. This layer will already receive the activation function that the user specifies in the external parameter of the HiddenActivation script. For example, I used Swish. I would recommend experimenting with all the activation functions you're using. At this stage, we want to verify the correctness of all the methods we've written so far. Exactly, the more diverse your testing is, the more potential issues you can address at this stage. This will help you avoid distractions during the actual training of the neural network and focus on improving its performance.
At this stage, we will not perform weight updates. Therefore, the specified method of updating the weights will not affect our testing results in any way.
//--- hidden layer
|
The third neural layer will contain only one output neuron and a linear activation function.
//--- result layer
|
Having collected a complete description of the neural network in a single dynamic array, we generate a neural network. To do this, we call the CNet::Create method of our base neural network class, in which the neural network is generated according to the passed description. At each step, we check the correctness of performing operations on the returned results. Receiving the boolean value true corresponds to the correct execution of the method's operations. If any of the errors occur, the method will return false.
We will specify the flag for using OpenCL. For full testing, we have to check the correctness of the backpropagation method in both modes of operation of the neural network.
//--- initialize the neural network
|
We conclude or work with the model creation procedure and move on to the main procedure of our OnStart script. In it, to create a neural network model, we just need to call the above procedure.
void OnStart()
|
At this stage, the neural network object is ready for testing. However, we still need initial data for testing. As mentioned above, we will simply populate them with random values. We will create the CBufferType data buffer to store a sequence of initial data. Target results are not of interest at this point. When generating the neural network, we filled the weight matrix with random values and do not expect to hit the target values. We also do not plan to train the neural network at this stage. Therefore, we will not waste resources on downloading unnecessary information.
//--- create a buffer to read the source data
|
In the loop, fill the entire buffer with random values.
//--- generate random source data
|
Now there is enough information to conduct a forward pass of the neural network. We will implement it by calling the FeedForward method of our neural network. The results of the direct pass will be stored in a separate data buffer of reference values. Probably the name reference for a randomly obtained result sounds strange. But within the scope of our testing, this will be the reference against which we will consider deviations when changing the input data or weights.
//--- perform a forward and reverse pass to obtain analytical gradients
|
In the next step, we add a small constant to the result of the feed-forward pass and run the backpropagation pass of our neural network to calculate the error gradients analytically. In the above example, I used the constant 1*10-5 as a deviation.
//--- create a result buffer
|
Please note that we need to keep the reference result unchanged. That's why we needed to create another data buffer object, into which we copied values from the benchmark values buffer. In this buffer, we correct the data for the backpropagation pass.
According to the results of the backpropagation pass, we will save the error gradients obtained analytically at the level of the initial data and weights. We also save the weights themselves, which we will need when analyzing the distribution of error gradients at the level of the weight matrix.
Perhaps it's worth mentioning that since we adjust the weights during the training process, obtaining accurate gradients at the weight matrix level is most informative for us. Accurate gradients at the level of input data mostly serve as indirect evidence of the correctness of gradient distribution throughout the entire neural network. This is due to the fact that before determining the error gradient at the level of the initial data, we have to consistently draw it analytically through all layers of our neural network.
We obtained the error gradients by an analytical method. Next, we need to determine the gradients empirically and compare them with the results of the analytical method.
Let's look at the initial data level first. To achieve this, we will copy our pattern of input data into a new dynamic array, which will allow us to modify the required indicators without the fear of losing the original pattern.
We will organize a loop to enumerate all the indicators of our pattern. Inside the loop, we will first add our constant 1*10-5 to each indicator of the original pattern in turn and implement a feed-forward pass neural network. After the feed-forward pass, we take the result obtained and compare it with the reference one that was saved earlier. The difference between the results of the feed-forward pass will be stored in a separate variable. Then we subtract a constant from the initial value of the same indicator and repeat the feed-forward pass. The result of the feed-forward pass is also comparable to the reference result. Let's find the arithmetic mean of two passes.
//--- in the loop, alternately change the elements of the source data and compare
|
pattern.m_mMatrix[0, k] = init_pattern.m_mMatrix[0, k] - delta;
|
At this point, you should be careful with the signs of the operation and deviations. In the first case, we added a constant and obtained some deviation in the results. The deviation is considered as the current value minus the reference.
In the second case, we subtracted the constant from the original value. Similarly, using the same formula for calculating the deviation, we will obtain a value with the opposite sign. Therefore, to combine the obtained results in magnitude and preserve the correct direction of the gradient, we need to subtract the second deviation from the first one.
The result is divided by 2 to get the mean deviation. The result obtained is comparable to the result of the analytical method.
We repeat the operations described above for all parameters of the initial pattern.
There is another aspect that we should take into account. The gradient indicates how the function value changes when the parameter changes by 1. Our constant is much smaller. Therefore, the empirically calculated gradient we obtained is significantly underestimated. To compensate for this, let's divide the empirically obtained value by our constant and display the total result in the MetaTrader 5 log.
//--- display the total value of deviations at the level of the initial data in the journal
|
Similarly, we determine the empirical gradient at the level of the weight matrix. Note that to access the matrix of weights, we obtain not a copy of the matrix but a pointer to the object. This is a very important point. Thanks to this, we can modify the values of weights directly in our script without creating additional methods to update buffer values in the neural network and neural layer classes. However, this approach is more of an exception than a general practice. The reason is that with this approach, we cannot track changes to the weight matrix from the neural layer object.
The cumulative result of comparing empirical and analytical gradients at the weight matrix level is also printed to the MetaTrader 5 log.
//--- reset the value of the sum and repeat the loop for the gradients of the weights
|
for(uint k = 0; k < weights.Total(); k++)
|
weights.Update(k, initial_weights.At(k) - delta);
|
After completing all the iterations, we clear the memory by deleting the used objects and exit the program.
//--- clear the memory before exiting the script
|
The results of my testing are shown in the screenshot below. Based on the testing results, I obtained a deviation in the 11th to 12th decimal place. For comparison, deviations in the 8—9th decimal places are considered acceptable in different sources. And it's not worth noting that when using OpenCL, the deviation turned out to be an order of magnitude smaller. This is not an advantage of using technology, but rather the influence of a random factor. At each run, a random matrix of weights and initial data was re-generated. As a result, the comparison was carried out on different parts of the neural network function with different curvature.

Results of comparing analytical and empirical error gradients
In general, we can say that the testing confirmed the correctness of our implementation of the error backpropagation algorithm both by means of MQL5 and using the OpenCL multi-threaded computing technology. Our next step is to assemble a more complex perceptron, and we will try to train it on a training set.