実践的なアドバイスをお願いします。

削除済み 2020.06.06 15:18

質問：結果を正しく評価するにはどうしたらよいですか？

各モジュールの誤差はパーセンテージで表示されます。0％が理想的な結果です。

パラメータ ______________________	モッド1	モッド2	モッド3	モード4	モード5	(vi) モード6	(vi) モード7	(vi) モード8	(vi) モッドナイン	(vi) モッド10	(vi) モッド11	(vi) モッド12	(八十三	(vi) 14	モード15	平均誤差	試行錯誤から
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

各モジュールの誤差は最小にしたいが、広がりも最小にしたい。

Alexandr Andreev 2020.06.06 15:50 #1

Сергей Таболин:

質問：結果を正しく評価するにはどうしたらよいですか？

各モジュールの誤差はパーセンテージで表示される。0％が理想的な結果です。

パラメータ ______________________	モッド1	モッド2	モッド3	モード4	モード5	(vi) モード6	(vi) モード7	(vi) モード8	(vi) モッドナイン	(vi) モッド10	(vi) モッド11	(vi) モッド12	(八十三	(vi) 14	モード15	平均誤差	試行錯誤から
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

各モジュールの誤差は最小にしたいが、広がりも最小にしたい。

対数積

ZS: 何が必要なのかよくわかりませんが、対数はエラーを漸進的に処理することができ、単一のケース（個々のモジュール）でより良い結果を得ることができます。そして、掛け算は分散を減らすための試み

削除済み 2020.06.06 16:05 #2

Alexandr Andreev:

対数積

ZS: 何が求められているのかよくわからないのですが、対数を使うことでエラーを漸進的に処理することができ、単一のケース（個々のモジュール）においてより良い結果を得ることができます。そして、マルチは普及を抑えるための試み

ありがとうございます。また、実際的には どうなのでしょうか？

Alexandr Andreev 2020.06.06 16:22 #3

Сергей Таболин:

ありがとうございます。それは実際どうなのでしょうか？

の製品だけだろう。

Option1 ) 各モジュールを(1-x%)のスタイルに変換して掛け合わせ...答えも単位から引きます。

x%はセルの値

オプション2

対数では、単純にセルの値を取って、そこから対数を数えます))) ゼロに近い値ほど漸進的な評価、つまりある基本設定において0.01より0.1の方が良く、1より0.1の方が良い。対数には基本パラメータしかありませんが、これは遊んでみる価値があります。

削除済み 2020.06.06 18:51 #4

Alexandr Andreev:

おそらく、シンプルな製品なら大丈夫でしょう。

Option1 ) 各モジュールを（1-x%）のスタイルに変換し、掛け合わせる...... 答えも単位から減算する。

x%はセルの値

オプション2

対数では、単純にセルの値を取って、そこから対数を数えます))) ゼロに近い値ほど漸進的な評価、つまりある基本設定において0.01より0.1の方が良く、1より0.1の方が良い。遊び甲斐のある対数の基底パラメータしかないでしょう。

オプション1

-3,43	-16,09	-14,82	-1,53	0,37	-16,72	-27,48	-4,70	-12,29	-4,70	-7,23	-5,33	0,37	-2,16	-5,96	10601305851,38
-4,06	-16,72	-11,66	-2,80	0,37	-18,62	-28,11	-3,43	-8,49	-4,06	-5,33	-5,33	-0,90	-0,90	-5,33	-6223799946,09
-3,43	-19,25	-15,46	-3,43	0,37	-16,72	-28,75	-5,33	-4,06	-7,23	-9,13	-4,06	0,37	-0,27	-3,43	1237520122,21

これは何を意味するのでしょうか？

オプション2

-0,64640373	-1,23274206	-1,19920648	-0,40312052	0,200659451	-1,24846372	-1,45453998	-0,75587486	-1,12352498	-0,75587486	-0,91539984	-0,80140371	0,200659451	-0,49968708	-0,84260924
-0,70415052	-1,24846372	-1,10243371	-0,5797836	0,200659451	-1,292699	-1,46404221	-0,64640373	-0,97726621	-0,70415052	-0,80140371	-0,80140371	-0,2787536	-0,2787536	-0,80140371
-0,64640373	-1,30642503	-1,21642983	-0,64640373	0,200659451	-1,24846372	-1,47348697	-0,80140371	-0,70415052	-0,91539984	-1,00560945	-0,70415052	0,200659451	-0,10380372	-0,64640373

これは底が0.1の対数です。

どうしたらいいのでしょうか？

他の機能も試しました。ただ、それもどう理解したらいいのか......。

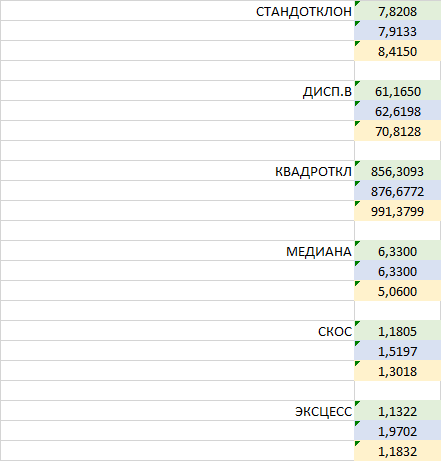
STANDOTCLONE	7,8208
	7,9133
	8,4150

DISP.B	61,1650
	62,6198
	70,8128

QUADROTKL	856,3093
	876,6772
	991,3799

メディヤナ	6,3300
	6,3300
	5,0600

スコー	1,1805
	1,5197
	1,3018

エクセス	1,1322
	1,9702
	1,1832

Practical advice, please. 静的配列 ? PREDICT time period

Dmitry Fedoseev 2020.06.06 18:58 #5

各行で最大値を求め、最大値が最小の行を選択する。駄洒落で失礼します))

削除済み 2020.06.06 19:12 #6

Dmitry Fedoseev:
各行で最大値を求め、最大値が最小の行を選択する。駄洒落で失礼します))

3行目で最大、1行目で最小の最大値。И?)))

Dmitry Fedoseev 2020.06.06 19:18 #7

Сергей Таболин:

3行目で最大、1行目で最小の最大値。И?)))

最初の行を選択します。

Alexandr Andreev 2020.06.06 21:15 #8

Сергей Таболин:

オプション1

-3,43	-16,09	-14,82	-1,53	0,37	-16,72	-27,48	-4,70	-12,29	-4,70	-7,23	-5,33	0,37	-2,16	-5,96	10601305851,38
-4,06	-16,72	-11,66	-2,80	0,37	-18,62	-28,11	-3,43	-8,49	-4,06	-5,33	-5,33	-0,90	-0,90	-5,33	-6223799946,09
-3,43	-19,25	-15,46	-3,43	0,37	-16,72	-28,75	-5,33	-4,06	-7,23	-9,13	-4,06	0,37	-0,27	-3,43	1237520122,21

これは何を意味するのでしょうか？

オプション2

-0,64640373	-1,23274206	-1,19920648	-0,40312052	0,200659451	-1,24846372	-1,45453998	-0,75587486	-1,12352498	-0,75587486	-0,91539984	-0,80140371	0,200659451	-0,49968708	-0,84260924
-0,70415052	-1,24846372	-1,10243371	-0,5797836	0,200659451	-1,292699	-1,46404221	-0,64640373	-0,97726621	-0,70415052	-0,80140371	-0,80140371	-0,2787536	-0,2787536	-0,80140371
-0,64640373	-1,30642503	-1,21642983	-0,64640373	0,200659451	-1,24846372	-1,47348697	-0,80140371	-0,70415052	-0,91539984	-1,00560945	-0,70415052	0,200659451	-0,10380372	-0,64640373

これは底が0.1の対数です。

どうしたらいいのでしょうか？

他の機能も試しました。でも、どうすれば彼らも理解できるのでしょうか？

面倒くさいな」「各モジュールの誤差はパーセンテージで表示されるんだ。0％が理想的な結果です」数字1は100％-x％または1-X*0.01を意味します。

Alexandr Andreev 2020.06.06 21:19 #9

セルゲイ・タボリン @Sergey Tabolin

															TOTAL
0,9557	0,8291	0,8418	0,9747	0,9937	0,8228	0,7152	0,943	0,8671	0,943	0,9177	0,9367	0,9937	0,9684	0,9304	0,77439
0,9494	0,8228	0,8734	0,962	0,9937	0,8038	0,7089	0,9557	0,9051	0,9494	0,9367	0,9367	0,981	0,981	0,9367	0,758606
0,9557	0,7975	0,8354	0,9557	0,9937	0,8228	0,7025	0,9367	0,9494	0,9177	0,8987	0,9494	0,9937	0,9873	0,9557	0,771806

2行目がベストで、1行目と3行目は非常によく似ています。

単位から引いた合計、つまり合計が0に近いほど良い結果になる...つまり、今までの結果は0.75があなたの75だからあまり良くない、でも何と比較するかによる...最悪のスコアは1（100%）で最高のスコアは0だ

99点より90点の方が10倍良いということを理解しないと...。99点なら99.9点より10倍いい...100点は、実はすべてのモジュールのエラースコアが100点のときだけ可能...」。つまり、0.1点は0.01点の10倍悪いと同時に、10点は1点の10倍悪いということです。

対数で考える......答えは、正の値ばかりになるはずだ......。通常、対数で1.1...を0〜1ではなく、1〜2の範囲にする...。を増やしたい場合は2、徐々に減らしたい場合は2より

二次偏差値方式は間違いなく論外です。偏差値をカウントしている他も同様です。なぜなら、理想的には線形回帰の二次偏差が分散を理解するために使われるはずだからです。でも、そうすると、数字そのものの平均が出ないまま、これらの偏差の推定値が出るわけで......。

Practical advice, please.

Roman 2020.06.07 01:48 #10

Сергей Таболин:

質問：結果を正しく評価するにはどうしたらよいですか？

各モジュールの誤差はパーセンテージで表示されます。0％が理想的な結果です。

パラメータ ______________________	モッド1	モッド2	モッド3	モード4	モード5	(vi) モード6	(vi) モード7	(vi) モード8	(vi) モッドナイン	(vi) モッド10	(vi) モッド11	(vi) モッド12	(八十三	(vi) 14	モード15	平均誤差	試行錯誤から
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

各モジュールの誤差は最小にしたいが、散らばりも最小にしたい。

モジュール誤差の二乗和を求め、その根を抽出するのがよいだろう。
こうして、モジュール全体の誤差の推定値を得ることになる。
この値はゼロに近いほど良い。
つまり、こんな感じです。

//+------------------------------------------------------------------+
//|                                                EstimateError.mq5 |
//|                        Copyright 2020, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2020, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"


double ModN[15][3] = {{4.43, 5.06, 4.43},
                      {17.09, 17.72, 20.25},
                      {15.82, 12.66, 16.46},
                      {2.53, 3.80, 4.43},
                      {0.63, 0.63, 0.63},
                      {17.72, 19.62, 17.72},
                      {28.48, 29.11, 29.75},
                      {5.70, 4.43, 6.33},
                      {13.29, 9.49, 5.06},
                      {5.70, 5.06, 8.23},
                      {8.23, 6.33, 10.13},
                      {6.33, 6.33, 5.06},
                      {0.63, 6.33, 0.63},
                      {3.16, 1.90, 1.27},
                      {6.96, 6.33, 4.43}};

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
{
   double ModX[];
   ArrayResize(ModX, 3);
   ZeroMemory(ModX);   
   
   int    num = 1;
   double est = 0.0;
   
   for(int i=0; i<15; i++)
   {
      for(int j=0; j<3; j++)
      {
         ModX[j] = ModN[i][j];         
      }
         
      est = EstimateError(ModX);  
      
      PrintFormat("Mod"+(string)num+" EstimateError: %.3f", est); 
      num++;
   }         
}// End OnStart

//+------------------------------------------------------------------+
double EstimateError(double & arr[])
{
   int size = ArraySize(arr);
   if(size == 0 || size < 3) 
      return(0.0);
   
   //double avg       = ArrayMean(arr); 
   double max       = ArrayMax(arr);   
   double min       = ArrayMin(arr); 
   double sum_sqr_e = 0.0;
   double est_e     = 0.0;      
   
   
   for(int i=0; i<size; i++)   
      sum_sqr_e += MathPow(arr[i] - (max-min)/* или avg*/, 2.0) / (size - 2.0);
      
   est_e = MathSqrt(sum_sqr_e);   

   return(est_e);
}

//+-------------------------------------------------------------------
//Возвращает максимальное значение элементов массива
double ArrayMax(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);          
   
   double max = arrIn[0];
   for(uint i=1; i<size; i++)
      if(arrIn[i] > max) 
         max = arrIn[i];

   return(max);
}

//--------------------------------------------------------------------
//Возвращает минимальное значение элементов массива
double ArrayMin(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);   
   
   double min = arrIn[0];  
   for(uint i=1; i<size; i++)
      if(arrIn[i] < min) 
         min = arrIn[i];

   return(min);
}

//--------------------------------------------------------------------
//Возвращает средне арефметическое значение элементов массива
double ArrayMean(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);         

   double sum = 0.0;       
   for(uint i=0; i<size; i++) 
      sum += arrIn[i];     
   
   return(sum/size);
}

//--------------------------------------------------------------------

2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod1 EstimateError: 6.965
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod2 EstimateError: 26.422
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod3 EstimateError: 19.577
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod4 EstimateError: 3.226
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod5 EstimateError: 1.091
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod6 EstimateError: 28.540
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod7 EstimateError: 48.234
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod8 EstimateError: 6.361
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod9 EstimateError: 6.102
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod10 EstimateError: 5.965
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod11 EstimateError: 8.130
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod12 EstimateError: 8.098
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod13 EstimateError: 7.198
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod14 EstimateError: 1.413
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod15 EstimateError: 6.138

推定では、Mod5が最も誤差が小さいことがわかる。

1 2 3 4 5 6 7

新しいコメント