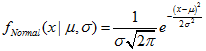#include <Graphics\Graphic.mqh>
#include <Math\Stat\Normal.mqh>
#include <Math\Stat\Math.mqh>
#property script_show_inputs
//--- 入力パラメータ
input double mean_value=0; // 期待値(平均)
input double std_dev=1; // 二乗平均平方根偏差(標準偏差)
//+------------------------------------------------------------------+
//| スクリプトプログラムを開始する関数 |
//+------------------------------------------------------------------+
void OnStart()
{
//--- 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//--- 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//--- 確率変数のサンプルを生成する
long chart=0;
string name="GraphicNormal";
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//--- 正規分布からサンプルを取得する
MathRandomNormal(mean_value,std_dev,n,data);
//--- ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//--- 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//--- [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityNormal(x2,mean_value,std_dev,false,y2);
//--- 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//--- チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
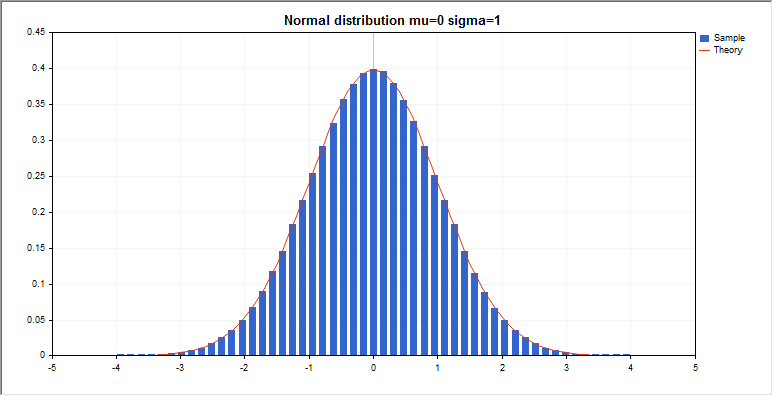
graphic.BackgroundMain(StringFormat("Normal distribution mu=%G sigma=%G",mean_value,std_dev));
graphic.BackgroundMainSize(16);
//--- カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,"Sample").HistogramWidth(6);
//--- 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,"Theory");
//--- カーブをプロットする
graphic.CurvePlotAll();
graphic.Update();
}
//+------------------------------------------------------------------+
//| データセットの頻度を計算する |
//+------------------------------------------------------------------+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//--- 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//--- 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+------------------------------------------------------------------+
//| シーケンス生成の値を計算する |
//+------------------------------------------------------------------+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//--- 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//--- 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//--- 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
}
|