Quantileバンド - MetaTrader 5のためのインディケータ

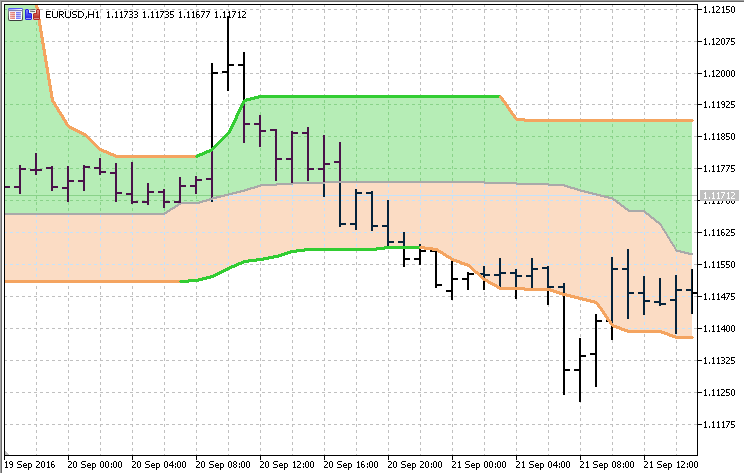
統計学と確率論では、分位数は確率分布を等しい確率を持つ連続区間に分割するか、サンプル内の観測値を同じ方法で分割するためのカットポイントです。分位数の数は作成されたグループの数より1つ少ないです。よって分位数とはデータセットを4つの等しいサイズのグループに分割する3つのカットポイントです（図示の例）一般的な分位数には、四分位、十分位（10個のグループを作成します。詳細は下記で）などの特殊な名前があります。作成されたグループは、半分、3分の1、4分の1などと呼ばれますが、分位数の用語が、カットポイントではなく作成されたグループに使用されることもあります。

q-分位数とは有限の値のセットを（ほぼ）同じサイズのqつのサブセットに分割する値です。 q-分位数はq − 1 あり、0 < k < qを満たす各整数ごとに一つあります。場合によっては、偶数サイズの一様分布上の一様確率分布の中央値（2分位数）の場合のように、ある分位数の値が一意に決定されない場合もあります。分位数は連続分布にも適用でき、ランク統計を連続変数に一般化する方法を提供します。確率変数の累積分布関数が知られている場合、q-分位数とは{1/q, 2/q, …, (q − 1)/q}の値への分位数関数（累積分布関数の逆関数 ）の適用です。