Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
La versione R 3.0.0 è ora disponibile.
Tutto deve essere reinstallato, compreso RStudio.
A proposito, qualcuno sa come sbarazzarsi delle 4 finestre obbligatorie.
faa1947:
A proposito, qualcuno sa come sbarazzarsi delle 4 finestre obbligatorie.
Trascinando i bordi verticali e orizzontali, puoi nascondere le finestre che non ti servono.
A proposito, se qualcuno è interessato
Tira su Renko sul grafico fino all'esatto primo ginocchio dello ZigZag da e verso il pick.
E sul ginocchio zero, vedi il ritardo o l'anticipo dell'inizio di Renko rispetto al picco dello Zigzag.
Il sistema è impostato come una fibra, ma il risultato è una curva nel seminterrato dal livello zero.
Non molto tempo fa il destino mi ha messo in contatto con questo argomento e subito sono sorte diverse domande. Cari esperti, potete aiutarmi a trovare risposte a queste domande? Non prendetemi a calci se qualcuna delle domande vi sembra stupida...
Quindi:
1) Ci sono diversi modi per trovare l'indice di Hurst. Quale di questi modi (secondo te) è il migliore (dà una stima più accurata dell'indice)? Se possibile, fornite un link alla fonte.
2) L'indicatore deve essere invariante sotto trasformazioni lineari? (Una risposta dettagliata è auspicabile).
3) Se le serie sono correlate tra loro, cosa si può dire dell'indice di Hurst?
4) Ci sono tre serie. Un indice Hurst è calcolato per ogni serie. Quando le serie vengono sommate, cosa si può dire dell'esponente?
Vi ringrazio in anticipo.
Dovremmo iniziare un thread separato sull'uso del linguaggio R? Condividere esperienze e risultati.
Naturalmente, se qualcuno è interessato.
Buona fortuna
Sono tornato di nuovo all'analisi di questo indicatore non banale. Per molto tempo sono stato confuso dal coefficiente laterale ottenuto calcolando il valore di Hearst. Essenzialmente, Hearst è un'equazione lineare in doppia scala logaritmica, dove sull'asse delle ordinate (Y) è data la distanza percorsa dal prezzo nelle scale corrette, e sull'asse delle ascisse (X) - un periodo specifico (timeframe o orizzonte). Questa equazione lineare è un'approssimazione dei punti che abbiamo misurato e tracciato sperimentalmente. La formula dell'equazione è semplice e ovvia:
Facciamo finta per un attimo che il coefficiente sia zero e semplifichiamo la formula a
sia zero e semplifichiamo la formula a 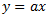 . Il valore
. Il valore 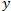 qui è la distanza percorsa dal prezzo. Il valore
qui è la distanza percorsa dal prezzo. Il valore 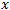 è il periodo di tempo. Ovviamente, in un classico moto browniano il prezzo percorre una distanza corrispondente alla radice quadrata di
è il periodo di tempo. Ovviamente, in un classico moto browniano il prezzo percorre una distanza corrispondente alla radice quadrata di  , dove
, dove 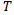 è il tempo o il periodo:
è il tempo o il periodo:
Questa equazione è un caso speciale della nostra formula, a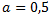 :
:
Questa formula in doppia scala logaritmica corrisponderà alla nostra funzione lineare propriamente detta:
Dove 0,5 è il coefficiente di Hurst.
Tutti questi calcoli sono banali, ma trascurano lo scomodo coefficiente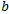 , che in realtà è quasi sempre un numero significativo. Le mie riflessioni matematiche sulla natura di questa dipendenza hanno portato alla comprensione di questo coefficiente. Dopo tutto, appare solo quando approssimiamo i nostri punti empirici con una funzione lineare. Per ogni punto particolare, la sua H è sempre nota. Non ha il coefficiente
, che in realtà è quasi sempre un numero significativo. Le mie riflessioni matematiche sulla natura di questa dipendenza hanno portato alla comprensione di questo coefficiente. Dopo tutto, appare solo quando approssimiamo i nostri punti empirici con una funzione lineare. Per ogni punto particolare, la sua H è sempre nota. Non ha il coefficiente perché non esiste nemmeno una funzione approssimativa generale per essa. Consideriamo un semplice esempio, proviamo a calcolare visivamente H per i punti C e D R/S del grafico EURUSD:
perché non esiste nemmeno una funzione approssimativa generale per essa. Consideriamo un semplice esempio, proviamo a calcolare visivamente H per i punti C e D R/S del grafico EURUSD:
Per il punto C è circa 0,45, per il punto D è 0,51. Poiché entrambi i punti giacciono quasi perfettamente sulla linea approssimata(y = 0,5304x - 0,0757 ) possiamo calcolare analiticamente i valori esatti di H per questi punti. Per C:
Per D:
Eseguendo la trasformazione inversa per D, per questo punto il valore Y è 1,5155 e il valore X corrisponde a 3, quindi la sua H sarà:
Il risultato del calcolo mostra che il punto C è antipersistente (H = 0,4547) e D è effettivamente browniano (H = 0,5051). La stima di H per l'intera serie diventa priva di significato, perché su un piccolo orizzonte la serie è antitrendy, mentre su un orizzonte più grande tende a diventare più trendy. Questo è pienamente coerente con le osservazioni empiriche sulle valute. Chiunque li scambi abbastanza a lungo vede che su piccole scale i prezzi fluttuano costantemente nel piatto, e su scale più grandi, che durano un anno o più, ci sono grandi movimenti di tendenza.
Il coefficiente è una specie di correzione relativistica in fisica. Forma una correlazione con H e determina il cambiamento del carattere del mercato con l'aumento della scala. Se questo coefficiente è vicino a zero, il mercato è omogeneo nella sua scala. La tendenza o l'antipersistenza in esso è approssimativamente allo stesso livello indipendentemente dalla scala. Se b è significativo - è la condizione iniziale dominante. H - inizia a dominare di più con l'aumentare della scala. Ecco i tipi di relazione tra H e
è una specie di correzione relativistica in fisica. Forma una correlazione con H e determina il cambiamento del carattere del mercato con l'aumento della scala. Se questo coefficiente è vicino a zero, il mercato è omogeneo nella sua scala. La tendenza o l'antipersistenza in esso è approssimativamente allo stesso livello indipendentemente dalla scala. Se b è significativo - è la condizione iniziale dominante. H - inizia a dominare di più con l'aumentare della scala. Ecco i tipi di relazione tra H e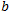 :
:
Se b modulo è una frazione significativa di H, allora non potete limitare la vostra analisi a H. Il mercato può mostrare due proprietà opposte su scale temporali diverse, ad esempio essere in tendenza e in controtendenza allo stesso tempo.
Se H e b sono significativi e puntano in direzioni diverse (H è significativamente più di 0,5 ed è negativo o H è significativamente meno di 0,5 e b è positivo) - il mercato mostra bruschi cambiamenti da uno stato all'altro a seconda del timeframe.
Qualcuno ha implementato la formula dell'indicatore di tempo mostrata qui:
http://cdn.scipeople.com/materials/2667/%D0%9F%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5%20RS%20%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0%20%D0%BD%D0%B0%20%D1%84%D0%BE%D0%BD%D0%B4%D0%BE%D0%B2%D1%8B%D1%85%20%D1%80%D1%8B%D0%BD%D0%BA%D0%B0%D1%85%202.doc
5 paesi