Matematica pura, fisica, logica (braingames.ru): giochi di cervello non legati al commercio - pagina 125
Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
Sembra che si adatti a tutte le opzioni in 2 pesate
questo disegno è qualcosa di alieno...
Strano, pensavo fosse più chiaro, penso che l'immagine sia più illustrativa delle parole. Ok, alcuni commenti:
Per la prima pesatura mettiamo due palline su ogni tazza della bilancia, in modo che in ogni tazza abbiamo 1 pallina del colore scelto e una pallina di qualche altro colore diverso dai colori delle palline nel cesto opposto. (Nella foto è una palla rossa con una verde e una palla rossa con una blu). I risultati di 1 pesata possono essere diversi: opzione 1.1) la bilancia è bilanciata e opzione 2) la bilancia è sbilanciata, una delle tazze supera 2.1). Cioè, abbiamo due rami della soluzione.
Se la prima variante, dividiamo le palline in due gruppi omogenei (gruppo ' e gruppo '), e poi 1.2) semplicemente pesiamo entrambi i gruppi (3 palline per tazza della bilancia) e determiniamo quale è pesante. Ecco, le palle pesanti sono state trovate.
La seconda opzione può avvenire in due casi (generalizzati). Quando entrambe le palline colorate della prima pesatura in ogni tazza sono pesanti o leggere. Con la (2.2) dopo aver marcato le palle in gruppi (gruppo ' e gruppo ') determiniamo con una sola pesata con una palla pesante, quale dei gruppi appartiene al gruppo pesante e quale a quello leggero.
Questa è una foto da internet....
Ok, alcuni commenti:
Ora lo schema è chiaro.
La seconda opzione può avvenire in due casi (generalizzati). Quando entrambe le palline colorate della prima pesatura in ogni tazza sono pesanti o leggere.
Strano, pensavo fosse più chiaro, penso che l'immagine sia più illustrativa delle parole. Ok, alcuni commenti:
Per la prima pesatura mettiamo due palline su ogni tazza della bilancia, in modo da avere in ogni tazza 1 pallina del colore scelto e una pallina di qualche altro colore diverso dai colori delle palline nel cesto opposto. (Nella foto è una palla rossa con una verde e una palla rossa con una blu). I risultati della prima pesatura possono essere diversi: opzione 1.1) la bilancia è bilanciata e opzione 2) la bilancia è sbilanciata, una delle tazze supera 2.1). Cioè, abbiamo due rami della soluzione.
Se la prima variante, dividiamo le palline in due gruppi omogenei (gruppo ' e gruppo '), e poi 1.2) semplicemente pesiamo entrambi i gruppi (3 palline per tazza della bilancia) e determiniamo quale è pesante. Ecco, le palle pesanti sono state trovate.
La seconda opzione può avvenire in due casi (generalizzati). Quando entrambe le palline colorate della prima pesatura in ogni tazza sono pesanti o leggere. Con la (2.2) determiniamo con una sola pesatura (gruppo ' e gruppo '), quale è quello pesante e quale è quello leggero.
Tieni i tuoi dubbi per te. CensuratoSenza offesa...
Opzione 1.1 che ho suggerito in privato. l'inizio è sbagliato.
Grazie per i complimenti, ragazzi, ma la verità viene prima!
In breve: due o tre?
Se due, datemi un diagramma, come io stesso so per tre.
Giusto grazie, poi il secondo ramo della soluzione diverge in tre opzioni (l'opzione c è aggiunta)
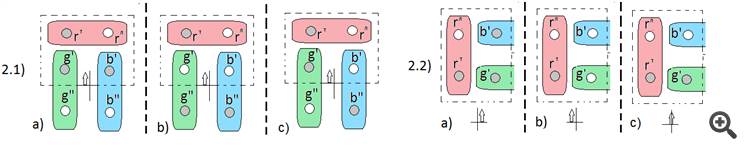
E la seconda pesatura sarà organizzata dalle stesse palle della prima, ma in una disposizione diversa. Di conseguenza, dopo la seconda pesata avremo una delle tre risposte, con cui possiamo ricostruire la posizione delle palline nella prima pesata, e conoscendo la pallina pesante della prima pesata (quella verde pesante) possiamo determinare il peso delle altre.Andrei, qual è la tua soluzione per le tre palle (basta la disposizione iniziale per ogni pesata)?
C'è l'opinione che ci siano diverse soluzioni.
Andrei, qual è la tua soluzione per tre palle (basta la disposizione iniziale per ogni pesata)?
Non ho un'opzione :) la soluzione sopra sembra essere corretta.
______________
E buon compleanno :) Più interessanti problemi di puzzle per te e per risolverli tutti.
Non ho un'opzione :) la soluzione di cui sopra sembra essere quella giusta.
______________
E buon compleanno :) Vi auguro molti problemi interessanti e che li risolviate tutti.
Grazie, Andrew.
Temo che dovrò postare più spesso quelli che non ho risolto. Ma risolveteli urgentemente (non mi piace leggere le soluzioni degli altri se non le ho risolte io stesso)!
P.S. Hai risolto il problema del 53?