Territorio di probabilità - pagina 8

[Yury Reshetov]

bowie:

L'algoritmo per vincere il gioco del lancio della moneta è semplice: se esce croce, scommetti su croce; se esce testa, scommetti su testa. Se il numero di lanci è infinito, si vince).

Se la moneta è storta, l'aspettativa è positiva. Questo è l'algoritmo di C. Shannon. Se la moneta è perfetta, allora lanciatela fino a perdere il cuore, l'aspettativa sarà zero, perché non dipende dal numero di prove.

[Ratibor Shokhirev]

Reshetov:
Если монетка кривая, тогда матожидание будет положительным. Это алгоритм К. Шеннона. Если монетка идеальная, то хоть до потери пульса подбрасывай, матожидание будет нулевым, т.к. оно не зависит от количества испытаний.

Shannon è senza dubbio una figata ottenere così tanti numeri in un solo posto. ) È più facile con una moneta. Code e teste formeranno "strisce di teste" e "strisce di code" se ci sono abbastanza lanci. Ogni volta che si scommette sul lato precedente il giocatore spera di entrare in una delle strisce di coda. L'aspettativa uguale a zero non è contestata. ) Un numero infinito di lanci permette al giocatore di fermarsi quando è abbastanza in più per lui.

Se il gioco permette di aumentare/diminuire le puntate prima di ogni lancio, un giocatore può aumentare la puntata dopo ogni vittoria e diminuirla dopo ogni perdita. Mi sembra che con tale approccio il payoff atteso sarebbe leggermente superiore a zero. A condizione che il capitale iniziale sia sufficiente).

[Yury Reshetov]

bowie:

Shannon è senza dubbio una figata ottenere così tanti numeri in un solo posto. ) È più facile con una moneta. Se vengono effettuati abbastanza lanci, testa e croce formeranno delle "strisce di testa" e delle "strisce di croce". Ogni volta che si scommette sul lato precedente il giocatore spera di entrare in una delle strisce di coda. L'aspettativa uguale a zero non è contestata. ) Il numero infinito di lanci permette al giocatore di fermarsi quando si trova nel plus sufficiente per lui.

Se il gioco presuppone la possibilità di aumentare/diminuire le puntate prima di ogni lancio, un giocatore può aumentare la puntata dopo ogni vittoria e diminuirla dopo ogni perdita. Mi sembra che con tale approccio l'aspettativa di vincita sarà un po' più alta di zero. Finché abbiamo abbastanza capitale iniziale.

La probabilità che il giocatore ottenga prima o poi il bordo a suo favore nel caso di una moneta perfetta è uguale a 1, cioè è vero secondo la legge di arcinoto. Che abbia un capitale sufficiente o meno è un'altra questione. La legge di arcinoto dice solo che il capitale a scommessa costante è inferiore all'infinito, per ottenere un vantaggio.

Una striscia, cioè una serie continua di teste e di code non contraddice nessuna teoria, ma i vantaggi non danno nemmeno. Se si è fortunati, si avrà un colpo di fortuna. Se sei sfortunato, avrai sfortuna. Non ha effetto sull'aspettativa matematica, ma solo sulla fortuna, cioè la varianza e la legge dell'arcsinus.

[Vasiliy Sokolov]

Reshetov:

La probabilità che un giocatore prima o poi ottenga un vantaggio nel caso di una moneta perfetta è 1, cioè è vero secondo la legge di arcinoto. Che abbia un capitale sufficiente o meno è un'altra questione. La legge di arcinoto dice solo che con una puntata costante, hai bisogno di meno di infinito per ottenere un margine.

Ma le strisce, cioè le serie continue di teste e code, non contraddicono nessuna teoria, ma non danno nemmeno un vantaggio. Chi è fortunato avrà un colpo di fortuna. Se sei sfortunato, avrai sfortuna. Non ha effetto sull'aspettativa matematica, ma solo sulla fortuna, cioè la varianza e la legge dell'arcsinus.

Reshetov, basta con le stronzate! Cosa c'entra la legge di Arcino? L'inizio della sovraperformance non significa che sarà sufficiente per spostarsi nella zona di rendimento positivo e non durerà abbastanza a lungo per mantenere quel rendimento nella zona positiva.

[Vladimir Gomonov]

C-4:
Reshetov, basta con le stronzate! Cosa c'entra la legge di Arcino? L'inizio di una sovraperformance nel proprio lato non significa che sarà sufficiente per spostarsi nella zona di rendimento positivo, né abbastanza a lungo per mantenere quel rendimento nella zona positiva.

Vi sbagliate entrambi :)

In realtà, tutte le monete sono storte, quindi Shannon ha ragione e anch'io. ;)

[Ratibor Shokhirev]

C'è uno script come questo. E ci sono dubbi su MathRand(). Chi può dire cosa? )

//+------------------------------------------------------------------+
//|                                                         Coin.mq5 |
//|                                                     [e-mail] |
//|                                                     [e-mail] |
//+------------------------------------------------------------------+
#property copyright "[e-mail]"
#property link      "[e-mail]"
#property version   "1.00"
#property script_show_inputs
input int attempt=8;//количество подбрасываний
input bool z=0;//первая ставка 1 или 0 (орел/решка)
input bool as=true;//true== увеличивать лот при каждом выигрыше/ false== уменьшать

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   bool win=z;
   uint prev_count=0,tickcount=0;
   int coin=-1; 
   //int attempt=y;
   int a_rate=0;
   int b_rate=0;
   double lot=1;
   double dep=256-1;
   double div=0.0;
   bool d  = (as==true) ? div=1.009 : div=0.009;
   for(int x=0;x<attempt;x++) 
   {
    tickcount=GetTickCount();    
    while(prev_count==tickcount)
    {tickcount=GetTickCount();}
    
    MathSrand(tickcount);
    coin=MathRand()+x;
    coin=MathMod(coin,2);
    //Print(coin);
    if(coin==1 && win==1){a_rate=a_rate+1;dep=dep+lot; lot=lot*div;}
    if(coin==0 && win==0){a_rate=a_rate+1;dep=dep+lot; lot=lot*div;}
    if(coin==0 && win==1){b_rate=b_rate-1;dep=dep-lot;lot=1;}
    if(coin==1 && win==0){b_rate=b_rate-1;dep=dep-lot;lot=1;}
    if(coin==1){win=1;}
    if(coin==0){win=0;}
    prev_count=tickcount;
   }
   Print("Подбрасываний= "+attempt);
   Print("Угаданных= "+a_rate);
   Print("Неугаданных= "+b_rate);
   Print("Деп= "+dep);
  }
//+------------------------------------------------------------------+

[Boris Odintsov]

07041982:

Propongo di discutere qui i metodi e le tecniche di utilizzo della teoria della probabilità per costruire sistemi di trading. Presenterò i miei pensieri su questo argomento sotto forma di tesi:

1) La probabilità di continuazione della tendenza in qualsiasi parte di essa in qualsiasi momento è superiore alla probabilità della sua inversione. Da qui, la regola d'oro del trader: fare trading solo con la tendenza.

2) La probabilità di vincere con un'entrata casuale e lo stesso TP e SL tende al 50% con SL e TP crescenti.

3) La probabilità di vincere quando si fa trading con un lotto dinamico è inferiore a quando si fa trading con un lotto fisso. Sono arrivato a questa conclusione da solo. Cercherò di dimostrarlo: diciamo che abbiamo TS, che ha innescato alternativamente TP e SL, cioè SL-TP-SL-TP-SL-TP, mentre SL = TP. Lo spread non è preso in considerazione per facilitare la comprensione. Quando si negozia con un lotto fisso, si ottiene per esempio: -$10+$10-10$+$10-10$+$10$=0. Quando si fa trading con lotto dinamico otterremo -10%+10%-10%+10%-10%+10%+10%+10%+10% e questo non ci porterà a zero profitti, ma sarà una perdita. Per esempio, il deposito era 100, abbiamo ottenuto: 100-10%=90; 90+10%=99; 99-10%=89.1; 89.1+10%=98.01; 98.01-10%=88.209; 88.209+10%=97.0299, che era necessario per dimostrare che la perdita è visibile.

Aspetto i vostri commenti e critiche costruttive se qualcuno non è d'accordo con la mia terza tesi. Se qualcuno ha altri pensieri sull'uso della teoria della probabilità, per favore parli.

Generalizzerò un po'.

Supponiamo che sl (perdita) e tp (profitto) siano fissati in punti di valuta.

Supponiamo di avere una serie sufficientemente grande di N scambi.

N=N1+N2, dove N1 - numero di operazioni eseguite su tp, N2 - numero di operazioni eseguite su sl.

Ovviamente, il vostro sistema di trading sarà redditizio se:

N1*tp - N2*sl >= spread * N

Dai, fai i conti: dividi le parti sinistra e destra per N.

tp*N1/N - sl*N2/N >= spread

N1/N con il numero di scambi che tende all'infinito non è altro che la probabilità di un affare redditizio, chiamiamola p=N1/N

N2/N - allora la probabilità di un trade perdente, e sarà uguale a 1-p

Abbiamo:

p*tp - (1-p)*sl >=spread

O in un altro modo:

p>=(sl + spread)/(sl+tp)

Questo è ciò per cui creiamo sistemi di trading. La probabilità che vogliamo aumentare. Ma dovremmo sempre ricordare cosa dovrebbe essere più che essere in profitto.

Per esempio, se ignorate lo spread, e con tp e sl uguali, il vostro sistema di trading sarà redditizio se p>0,5 ... ecc.

Se fai dei cambiamenti come il lotto dinamico, allora le cose diventano molto più complicate, e la probabilità di un trade redditizio dovrebbe essere più alta che nel caso precedente.

[John]

bobsley:

Generalizzerò un po'.

Se generalizziamo un po' di più e prendiamo in considerazione la situazione reale 1) Dobbiamo considerare gli swap 2) Se esprimiamo SL e TP attraverso lo spread nella tua formula, otteniamo

p>= ( n_SL*spread + spread ) / (n_TP*spread + n_SL*spread) => p >= spread*(n_SL+1) / spread*(n_TP+n_SL) => p >= (n_SL+1)/(n_TP+n_SL)

Se lo disegniamo come un grafico, vedremo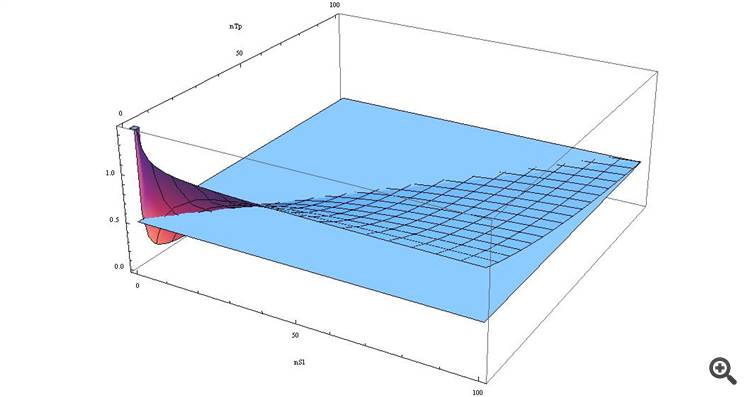

Vediamo che con SL > TP la nostra funzione è maggiore di 0,5, e più questi valori sono vicini...

Quelli che vogliono vedere da soli - ecco la formula in termini di Wolfram-Alpha

g1 = Plot3D[(1 + nSl)/(nSl + nTp), {nSl, 0, 100}, {nTp, 0, 100}, AxesLabel -> Automatic]; 
g2 = Graphics3D[{Polygon[{{0, 0, 0.5}, {100, 0, 0.5}, {100, 100, 0.5}, {0, 100, 0.5}}], Polygon[{{0, 0, 0.9}, {100, 0, 0.9}, {100, 100, 0.9}, {0, 100, 0.9}}]}];
Show [{g1, g2}]

Una conclusione inaspettata per molte persone, vero?)

Mi ricordo che molto tempo fa, qui alcune persone gridavano - quello che sto dicendo qui, che "SL è il male". :))

Così ora i giovani sono qui e sono più informati ora. :)

[Mykola Demko]

bobsley:

Generalizziamo un po'.

Che sl (perdita) e tp (profitto) siano fissati in punti di valuta.

...

Se si fanno dei cambiamenti come un lotto dinamico, allora le cose si complicano notevolmente e la probabilità di un trade redditizio dovrebbe essere maggiore che nel caso precedente.

Come formula puramente teorica è ovviamente interessante, ma!!!

Se si fanno cambiamenti come il lotto dinamico, tutto diventa molto più complicato...

E se il profitto/perdita non è fisso (ma diverso per tutti i trade), diventerà ancora più complicato, e poi ci aggiungiamo lo spread fluttuante - otterremo un tale casino che 10 sviluppatori di EA lo spargeranno su tutto il tavolo per anni.

Per questo ho cercato di spiegare che è difficile far funzionare il mercato con valori di take/loss fissi. Fissando i valori, lo sviluppatore del sistema tarpa le ali al sistema (formalmente parlando, non fa profitto).

E tp e sl come livelli fissi sono necessari solo per proteggere l'account da perdite in caso di disconnessione. Ma ci sono soluzioni più semplici del fissaggio.

Per esempio, per gli stop reali è sufficiente impostare uno stop mobile bidirezionale a strascico dietro il mercato e non scatta mai finché c'è una connessione, e fare trading in base alla situazione.

Questa è la mia opinione.

[Avals]

MetaDriver:

Vi sbagliate entrambi :)

In realtà, tutte le monete sono storte, ecco perché Shannon ha ragione, e anche io. ;)

In realtà, le monete cambiano la loro curvatura mentre vengono testate). Perché non si può ripetere l'esperimento esattamente nelle stesse condizioni del precedente. I fattori casuali cambiano e può darsi che la loro curvatura risultante sia sbilanciata per molto tempo. Cioè, è una questione di tasso di cambiamento dei fattori casuali rispetto all'esperimento. Come il loro tempo interno è correlato al tempo tra gli esperimenti.

Supponiamo per esempio che un processo casuale sia generato sulla base di una singola sinusoide. Se al momento dell'esperimento il valore del seno>0, allora testa, meno di quello - croce. E poi tutto dipenderà dalla periodicità dei nostri esperimenti, dalla precisione del calcolo del tempo e dal periodo della sinusoide. Se gli intervalli tra gli esperimenti non sono fissi e sono molto più lunghi del periodo della sinusoide, allora i valori appariranno come casuali. Se il tempo tra gli esperimenti può essere regolato con una precisione commisurata al periodo dell'onda sinusoidale, la serie sarà non casuale - fino a deterministica (a seconda della precisione della misura del tempo).

In generale, i processi casuali possono non essere periodici, ma la ciclicità di essi e la somma di tutti i fattori casuali devono essere presenti. Per esempio, non ci può essere una funzione continuamente crescente invece di una sinusoide - allora la serie risultante avrà una tendenza all'aumento. I processi casuali che influenzano la serie sono infatti tutti non casuali)))) solo che non ci sono informazioni per misurare accuratamente la loro fase al momento dell'esperimento, o non c'è sufficiente precisione di misura.

Se la somma dei fattori "casuali" è equilibrata rispetto a 0 (come nell'esempio con la sinusoide) - cioè se è sopra 0 e sotto 0, allora la serie sotto l'influenza di questi fattori avrà mo = 0. Se la somma è superiore a 0 per un tempo più lungo, ci sarà uno skew a favore di teste o a favore di code. Cioè la somma dei fattori casuali è in un certo senso equilibrata e ciclica. Solo che non conosciamo il suo valore esatto al momento dell'esperimento.

Ma la realtà è complicata dal fatto che i fattori casuali possono cambiare e così la loro somma. Prima era un'onda sinusoidale)) poi è diventata una linea retta ad angolo se in quelle analogie. Ecco perché il compito del trading è quello di cogliere questi momenti quando la serie ha una componente di tendenza che va verso l'alto o verso il basso. Questo richiede la corrispondenza con i processi sottostanti. I processi di ritorno come una sinusoide formano modelli di ritorno (come il trading piatto), i processi obliqui formano la deriva (tendenza). In generale, il compito è quello di riconoscere un processo in una delle sue fasi conoscendo quella successiva. La difficoltà è che ci sono molti di questi mini-processi e sono di scala diversa, e con il tempo la loro influenza cambia semplicemente (ampiezza se nel quadro dell'analogia con un'onda sinusoidale).