Hurst Exponent - indicatore per MetaTrader 5

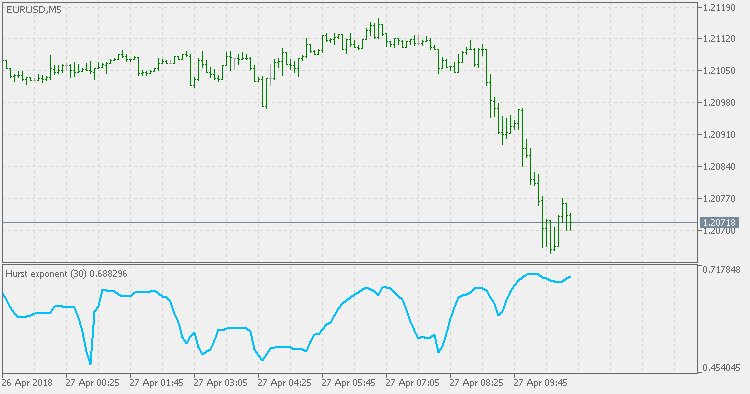
The Hurst Exponent is used as a measure of long-term memory of time series. It relates to the autocorrelations of the time series, and the rate at which these decrease as the lag between pairs of values increases. Studies involving the Hurst exponent were originally developed in hydrology for the practical matter of determining optimum dam sizing for the Nile river's volatile rain and drought conditions that had been observed over a long period of time. The name "Hurst exponent", or "Hurst coefficient", derives from Harold Edwin Hurst (1880 - 1978), who was the lead researcher in these studies; the use of the standard notation H for the coefficient relates to his name also.

The Hurst exponent is referred to as the "index of dependence" or "index of long-range dependence". It quantifies the relative tendency of a time series either to regress strongly to the mean or to cluster in a direction.

• A value of H in the range 0.5 - 1 indicates a time series with long-term positive autocorrelation, meaning both that a high value in the series will probably be followed by another high value and that the values a long time into the future will also tend to be high.
• A value of H in the range 0 - 0.5 indicates a time series with long-term switching between high and low values in adjacent pairs, meaning that a single high value will probably be followed by a low value and that the value after that will tend to be high, with this tendency to switch between high and low values lasting a long time into the future.
• A value of H = 0.5 can indicate a completely uncorrelated series, but in fact it is the value applicable to series for which the autocorrelations at small time lags can be positive or negative but where the absolute values of the autocorrelations decay exponentially quickly to zero. This in contrast to the typically power law decay for the 0.5 < H < 1 and 0 < H < 0.5 cases.