Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
J'essaie de comprendre l'origine de vos nombres x et P(x), je pense que l'anglais n'est peut-être pas votre première langue, donc je veux m'assurer que nous comprenons la signification des termes que vous utilisez avant de faire des conclusions ou des déclarations confuses.
"avec un risque constant de 0,5% par transaction"
Qu'est-ce que 0,5 % de risque par transaction ? Cela signifie-t-il que vous risquez 0,5 % du solde du compte dans le cas où le marché évolue contre votre position et que celle-ci est fermée au prix du stoploss ?
"Cela signifie que j'ai un risque de 0,35% d'être à 50% du solde de mon compte"
Le risque de ruine est un calcul du facteur temps, ce qui signifie que les unités sur le relevé que vous faites avec les chiffres que vous calculez sont destinées à être un "par transaction" ou "par semaine" ou "par mois".
Pour l'instant, je ne peux pas dire d'où viennent x et P(x) mais cela détermine les unités impliquées ici.
Aidez-moi à comprendre ce que vous avez fait et je serai plus qu'heureux d'investir le temps nécessaire pour déterminer si vous appliquez les calculs correctement.
salut philip
et merci de m'avoir aidé ici :)
0,5% de risque par transaction signifie exactement cela. C'est le montant que je perds si le marché va à l'encontre de ma position et atteint le SL.
La valeur de 0,35% est pour la période de l'ensemble du test (qui est une période d'environ 8 ans.... ), X et P(X) sont tous deux tirés de ce rapport ainsi.
Je n'arrive pas à comprendre pour quelle période de temps il serait logique de faire ce calcul !
Prenons la période du 10.01.2001 au 10.01.2002.
Serait-il logique de calculer le facteur sur cette période ? Y a-t-il assez de données ici pour déterminer la relation entre les trades gagnants et perdants... ?
J'espère avoir été clair cette fois-ci :)
La façon dont vous utilisez les calculs de risque de ruine est de définir une période de temps (mensuelle, hebdomadaire, annuelle, etc.), ou un incrément quelconque (par transaction, par 10 transactions, etc.), puis vous rassemblez les statistiques pour ces périodes. Il est important de savoir ce que le résultat du calcul du risque de ruine signifie réellement (ses unités).
Parfois, il est utile de s'assurer d'abord que vous posez la bonne question (en d'autres termes, assurez-vous que la réponse que vous essayez de calculer va réellement répondre à la question à laquelle vous voulez répondre).
Par exemple, mes clients fonctionnent sur une base mensuelle. Ils ne se soucient pas de l'aspect quotidien ou hebdomadaire, pour eux, tout ce qui compte, ce sont les résultats mensuels. Dans mon cas, il n'est donc pas utile que je calcule le risque de ruine pour les résultats hebdomadaires ou pour chaque transaction.
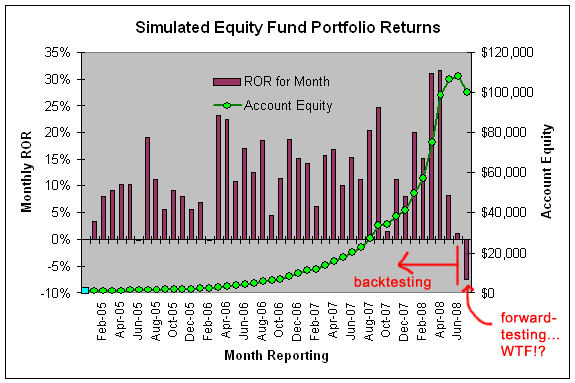
En conséquence, ce que je dois faire dans le backtest, c'est capturer le taux de rendement moyen (profits, pertes, ROR, etc.) sur une base mensuelle. Quelque chose comme ce qui suit :
Pour calculer le risque de ruine, vous devez d'abord rassembler les données pour votre période de temps. Dans mon cas, dans cet exemple, je devais rassembler les résultats des taux de rendement mensuels, calculer le ROR mensuel moyen, puis calculer l'écart type de ces taux de rendement mensuels.
Dans cet exemple, le taux de rendement mensuel moyen était de 12 % avec un écart type de 8 %... d'après les résultats du backtesting, cela aurait dû être une valeur sûre pour l'avenir, mais ce n'est pas le cas (comme vous pouvez le voir). Notez que je fais référence au risque de ruine en tant que risque de perte (ROL) car je ne suis pas intéressé à savoir quand mon compte sera ruiné (c'est la question triviale) mais plutôt à savoir à quelle fréquence je dois m'attendre à ce que le compte soit sous-dimensionné d'un montant fixe, disons 20%.
Ainsi, un taux de rendement mensuel de 12 % avec un écart type de 8 % signifie que je peux m'attendre à ce que mon compte subisse une perte de valeur de 7,4 % environ 6,5 % du temps (6,5 % des événements de fin de mois, soit environ une fois tous les 15 mois).
Ainsi, alors que j'ai été initialement pris au dépourvu par le résultat apparemment inexplicable du test avant, il était parfaitement raisonnable de s'attendre à un tel résultat mensuel sur la base des résultats du backtesting, une fois tous les 15 mois je peux m'attendre à un tel drawdown négatif sur le point culminant de mon compte.
Vous voyez donc que pour calculer une évaluation significative du risque de perte, vous devez d'abord décider quelle période est pertinente pour vous, puis vous devez rassembler les résultats sous une forme qui permette de calculer la moyenne et l'écart type du RdR sur cette période.
Une fois que vous avez les données du backtest, vous pouvez alors effectuer une myriade d'analyses statistiques en utilisant les calculs du risque de ruine (ou du risque de perte comme j'aime l'appeler).
J'ai beaucoup de questions !
pour commencer....
1- Dans vos calculs mensuels, supposez-vous une taille de position constante ?
2- Chaque test mensuel est-il effectué sur le dépôt initial ? indépendamment de la progression des mois précédents ?
en supposant que la réponse aux deux premières questions est OUI :)
J'ai calculé le ROR pour 14 groupes de 100 transactions.
J'ai utilisé une taille de lot de 0,01 et j'ai fait le calcul sur le dépôt initial de 700 $ pour chaque groupe.
et j'ai obtenu les résultats suivants :
(Je dois installer Excel, n'est-ce pas ? )
1-> 0%
2-> + 12%
3-> 0%
4-> + 18%
5-> - 3%
6-> -8%
7-> +22%
8-> -3%
9-> +11%
10-> +23%
11-> +17%
12-> +7%
13-> -8%
14-> +2%
à partir de ces données, j'ai obtenu un ROR moyen de 6,5% avec un écart type de 10,47%.
Maintenant, je ne sais pas comment calculer la deuxième partie :
"Donc un ROR mensuel de 12 % avec un écart type de 8 % signifie que je peux m'attendre à ce que mon compte subisse une perte de valeur de 7,4 % environ 6,5 % du temps (6,5 % des événements de fin de mois, soit environ une fois tous les 15 mois)."
J'ai beaucoup de questions !
pour commencer....
1- Dans vos calculs mensuels, supposez-vous une taille de position constante ?
2- Chaque test mensuel est-il effectué sur le dépôt initial ? indépendamment de la progression des mois précédents ?
Oui, le backtesting DOIT toujours être effectué sans compounding si vous souhaitez éliminer le biais de la chronologie des événements de l'analyse. Nous devons accorder à chaque événement (transaction) la même pondération qu'à tous les autres événements si nous avons l'intention d'utiliser des analyses statistiques non pondérées (telles que la moyenne, l'écart-type, etc.). Je pense que vous en êtes déjà conscient.
Lorsque vous effectuez des tests prospectifs ou des tests en direct, vous devez faire un choix : voulez-vous que le test prospectif serve uniquement à gagner de l'argent (la capitalisation devrait alors être effective) ou voulez-vous que le test prospectif génère des données qui se prêtent à ce type d'analyses statistiques ?
Je dois noter que dans la limite mathématique de la période d'échantillonnage devenant suffisamment petite pour capturer une transaction, les facteurs de biais statistique vont à l'unité (un), donc les erreurs introduites en ignorant le fait que le biais statistique est en vigueur peuvent être minimes dans ces situations.
Le but de tout ce charabia est de dire que vous avez des décisions à prendre, à la fois en ce qui concerne vos backtests et vos tests prospectifs (ou trading en direct) et si vous souhaitez que les statistiques entre les deux soient comparables au sens mathématique, vous devez vous assurer que vous avez géré le backtest de manière à ce que les données résultantes puissent être mises en correspondance (un autre terme mathématique) avec les statistiques pertinentes pour les tests prospectifs.
Effectuer les backtests avec une taille de lot fixe invariable par rapport au solde du compte de départ est la seule façon de procéder dans le backtest.
en supposant que la réponse aux deux premières questions est OUI :)
J'ai calculé le ROR pour 14 groupes de 100 transactions.
J'ai utilisé une taille de lot de 0,01 et j'ai fait le calcul sur le dépôt initial de 700 $ pour chaque groupe.
et j'ai obtenu les résultats suivants :
(Je dois installer Excel, n'est-ce pas ? )
1-> 0%
2-> + 12%
3-> 0%
4-> + 18%
5-> - 3%
6-> -8%
7-> +22%
8-> -3%
9-> +11%
10-> +23%
11-> +17%
12-> +7%
13-> -8%
14-> +2%
à partir de ces données, j'ai obtenu un ROR moyen de 6,5% avec un écart type de 10,47%.
Maintenant, je ne sais pas comment calculer la deuxième partie :
"Donc un ROR mensuel de 12 % avec un écart type de 8 % signifie que je peux m'attendre à ce que mon compte subisse une perte de valeur de 7,4 % environ 6,5 % du temps (6,5 % des événements de fin de mois, soit environ une fois tous les 15 mois)."
Une fois que vous avez les données du backtest, et à condition que les données soient préparées comme indiqué dans le post ci-dessus, vous pouvez choisir l'équation que vous souhaitez utiliser pour calculer votre risque de perte future.
Allez-vous utiliser les intérêts composés ou non ? Si vous n'avez PAS l'intention d'utiliser la capitalisation, l'équation est simple, comme suit :
Nous calculons donc votre R (la fréquence à laquelle vous pouvez vous attendre à ce que votre compte baisse de 10 % après 100 transactions) comme suit :
Ainsi, dans cet exemple, la question étant "à quelle fréquence puis-je m'attendre à ce que mon compte subisse une baisse d'au moins 10 % par rapport au point culminant après 100 transactions", la réponse est "30,5 % du temps".
Ou encore, vous pourriez dire "mon compte devrait subir une baisse de 10 % par rapport à son point culminant au moins une fois toutes les trois périodes de 100 transactions". Et ce, si vous ne pratiquez pas la capitalisation.
Si vous avez l'intention de faire du compounding sur votre compte pour des tests prospectifs ou des tests en direct, vous utilisez les mêmes RdR% et stand-dev (puisque vous les avez générés sans biaiser la chronologie des événements, ils peuvent également être mis en correspondance avec cette utilisation), vous utilisez alors simplement la formule plus compliquée :
. Et donc, nous calculons R pour une méthode d'échange composée qui est construite sur une stratégie d'échange telle que vous l'avez développée et nous obtenons :
. Dans ce cas, la différence entre la capitalisation et la non-composition fait peu de différence pour le risque de perte calculé (30,6 % contre 30,5 %), comme prévu, mais la capitalisation sera toujours moins performante que la non-composition (statistiquement du moins) si votre ratio de Sharpe est <1 (le vôtre est de 0,62, bien inférieur à 1).
Je ne suis pas sûr que nous soyons sur la même longueur d'onde...
les formules sont assez familières...
Cependant, cela a-t-il vraiment du sens d'avoir 30,5 % de chances de perdre au moins 10 % du solde du compte pour la distribution des valeurs en cours ?
considérez le fait que pour cet ensemble de 14 valeurs, le drawdown maximum était de 8% qui s'est répété seulement deux fois et jamais en dessous !
donc les 30.5% pour avoir un drawdown de 10%+ semblent tout à fait hors de proportion ici...
J'ai fait ma propre petite recherche et j'ai essayé de calculer la probabilité d'avoir un drawdown de 10%+ et j'ai obtenu un résultat différent.
J'ai utilisé la formule suivante :
X est une variable aléatoire issue d'une distribution normale avec une moyenne μ et un écart-type σ.
X = - 10%
µ = 6.5%
σ = 10.47%
En raison de la nature symétrique de la distribution normale, je peux utiliser + 1,576.
La probabilité cumulative jusqu'à Z est donnée par -> Φ(t)=P(Z≤t)
mais je dois calculer le cumulatif complémentaire qui est 1-Φ(t) = 1 - P(1.576) = 1 - 0.9418 = 0.0582 = 5.8%.est-ce que cela a un sens ? ? parlons-nous de la même chose ?
X est une variable aléatoire issue d'une distribution normale de moyenne μ et d'écart-type σ.
X = - 10%
µ = 6.5%
σ = 10.47%
mais je dois calculer le cumulatif complémentaire qui est 1-Φ(t) = 1 - P(1.576) = 1 - 0.9418 = 0.0582 = 5.8%.cela a-t-il un sens ? ? parlons-nous de la même chose ?
µ est-il ici le drawdown moyen ou le taux de rendement moyen ? Et σ est-il ici l'écart-type du drawdown ou l'écart-type du taux de rendement ? Le cumulatif complémentaire est-il la probabilité d'un drawdown de 10% ou la probabilité d'un taux de rendement de -10% ?
Si je comprends bien, vous confondez vos valeurs de risque de rendement avec celles du risque de drawdown. Si vous voulez calculer les statistiques du risque de drawdown, vous devez calculer le drawdown pour chaque trade (pas le profit/la perte, mais le drawdown transitoire pendant que le trade était "live") de sorte que vous puissiez ensuite calculer le drawdown moyen par trade et le stddev, puis la valeur cumulative complémentaire représentera ce à quoi vous pensez.
Nous parlons du risque de ruine (plus précisément du risque de perte, un cas encore plus généralisé du calcul du risque de ruine). Lisez cet article, je veux dire lisez-le vraiment et ne vous contentez pas de gloser sur les nuances spécifiques des mots employés.
À la page deux, nous avons le calcul très simple du risque de perdre 1-sigma, votre sigma est de 10,47%. Le risque de perdre 10,47% dépend de votre taux de rendement moyen, qui est de 6,5% dans votre cas. Votre sharpe est inférieur à 1 (ce qui n'est généralement pas considéré comme une bonne chose) et votre risque de perdre 10,47 % (1-sigma) est de 29,1 %.
Prenez note de l'ordonnée et de l'abscisse de ce graphique, les gens s'y perdent tout le temps. L'axe des ordonnées devrait susciter quelques questions clés dans votre esprit, et y répondre vous permettra de comprendre ce que signifie le drawdown. Demandez-vous "comment se fait-il que j'aie une probabilité proche de 100 % de subir une perte de 0,1 %".
Pensez-y, pensez à ce que nous calculons avec le risque de perte/ruine, pensez à ce à quoi ressemble le graphique de l'équité de votre transaction en fonction du temps et réalisez qu'à chaque fois qu'elle atteint un nouveau sommet et qu'elle recule un tant soit peu, ce tant soit peu léger recul est un drawdown par rapport au nouveau sommet.
Quoi qu'il en soit, les gens n'ont pas tendance à envisager le risque de perte en termes de 1-sigma, mais ils ont tendance à penser en termes de 50/50, comme un tirage au sort. Quel est donc le montant d'équité que votre compte risque de perdre 50 % du temps ? Réponse : 6%
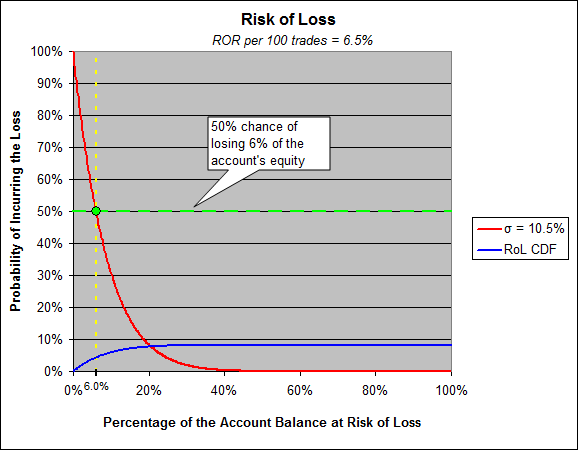
Vous avez une chance sur deux de perdre 6% à la fin d'une série de 100 transactions.
Comprenez également que ce calcul est basé sur les statistiques de seulement 14 échantillons, généralement nous nous référons aux nombres produits par ces calculs comme des "limites inférieures". En d'autres termes, si nous calculons que vous risquez de perdre 6% de votre capital dans 50% des cas, nous considérons que cette valeur signifie "au moins 6%, mais probablement plus en raison de facteurs de risque non pris en compte".
Il y a une raison pour laquelle 75% des gens perdent de l'argent sur le marché des changes malgré des backtests montrant que leur stratégie est le Saint Graal. Les données sont à leur disposition (c'est-à-dire qu'ils pourraient générer les données nécessaires) pour calculer le risque de ruine, mais ils se laissent convaincre par l'espoir et les rêves que représentent le facteur de profit et le gain attendu, etc.
Mais ne me croyez pas sur parole, vous avez l'article, allez voir David et demandez-lui, il aime en parler. Et mettez-la à l'épreuve. Prenez votre stratégie backtestée et mettez-la dans un test avant et regardez ce qui se passe. (Vous avez regardé mes résultats ci-dessus lorsque j'ai involontairement fait cette expérience moi-même).
(et il y a une autre pépite d'épiphanie financière à découvrir dans les analyses de risque de perte, vous découvrirez pourquoi le ratio de Sharpe est si vénéré parmi les analystes financiers, puis vous vous rendrez compte de sa principale faiblesse et pourquoi les gens disent que "le bêta tue")
OK
Je crois que j'ai compris.
Je reviendrai demain avec d'autres questions :)
Oh...
Il y a une chose que je ne comprends toujours pas : ..... N'y a-t-il pas d'autres facteurs qui influencent ce calcul ?
Prenons vos résultats ROR calculés sur une base mensuelle.
Supposons (pour les besoins de l'argumentation) que plus il y a de transactions dans un mois, plus le ROR est élevé.
par exemple : pour 0 transaction, vous gagnez 0%.
pour 10 transactions vous gagnez 5% (en moyenne)
pour 20 transactions, vous gagnez 10% (en moyenne)
et ainsi de suite...
Supposons que pour cette période de 30 mois, il y ait une grande dispersion des valeurs dans la distribution du ROR (pour chaque mois, il y a un nombre complètement différent de trades effectués).
de sorte que le rendement moyen soit de 10 % et l'écart type de 20 % et qu'il n'y ait pas de ROR négatif (on ne peut pas avoir un nombre négatif de transactions...).
Maintenant, le calcul du risque de perte d'un écart-type de 20% nous donne approximativement 37% ... ce qui n'a pas vraiment de sens...
Vous voyez où je veux en venir ?