Pouvez-vous me dire comment calculer la distance entre deux lignes parallèles en tenant compte de l'échelle du graphique (pour que l'échelle ne soit pas affectée) ?
Voici un exemple :
La ligne rouge est la distance entre deux lignes parallèles - comment pouvez-vous la calculer ?
Vous devez mesurer la distance en un point de l'axe X - c'est votre moment, je suppose...
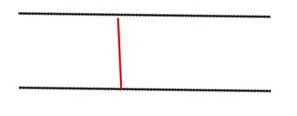
Ou bien devez-vous mesurer réellement avec un offset ? Alors par le théorème de Pythagore - vous connaissez deux côtés et un angle...
Cela dépend aussi de la distance - en pixels ? Il faudrait alors commencer par tout traduire dans le système de coordonnées approprié.Pouvez-vous me dire comment calculer la distance entre deux lignes parallèles en tenant compte de l'échelle du graphique (pour que l'échelle ne soit pas affectée) ?
Voici un exemple :
La ligne rouge est la distance entre deux lignes parallèles - comment la calculer ?
Pour que l'échelle ne soit pas affectée, vous devez utiliser une échelle fixe sur le graphique. Sinon, elle sera toujours affectée.
Salut !
Et comment un tel système de coordonnées peut-il être construit, comment l'imaginez-vous ?
Vous devez mesurer la distance en un point de l'axe X - c'est votre temps, je suppose...
Ou devez-vous mesurer avec un offset ? Alors par le théorème de Pythagore - vous connaissez deux côtés et un angle...
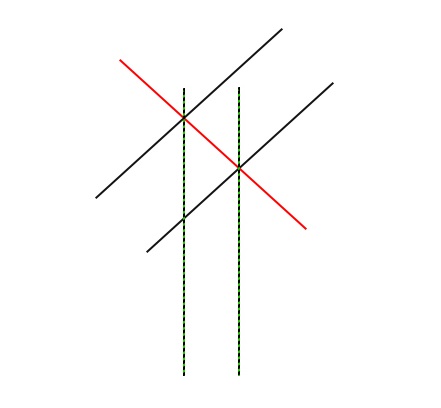
Et cela dépend aussi de la distance - en pixels ? Ensuite, vous devrez tout convertir dans le système de coordonnées approprié pour commencer.Si l'on réfléchit logiquement, la ligne rouge devrait être perpendiculaire aux deux lignes (noires) - ce qui permettrait de mesurer la distance. Peu importe la valeur qui sera mesurée, le plus important est que lorsque vous changez d'échelle, cette valeur ne change pas.
J'ai même essayé de le faire de cette façon : prendre la valeur du franchissement de ligne et compter le nombre de barres entre elles ... Cette approche n'est pas adaptée au changement d'échelle !
Pour que l'échelle ne soit pas affectée, il est nécessaire d'utiliser une échelle graphique fixe. Sinon, elle sera toujours affectée.
Pourquoi ? Qu'en est-il de la proportion ?
Itum:
Je ne me soucie pas de la valeur dans laquelle cette valeur sera mesurée, le plus important pour moi est que cette valeur ne change pas lorsque vous changez d'échelle.
Dans ce cas, il suffit de le mesurer en pips. Les lignes sont fixées au prix et lorsque vous changez d'échelle, la distance entre elles ne change pas, cela ne change que la représentation visuelle des lignes.
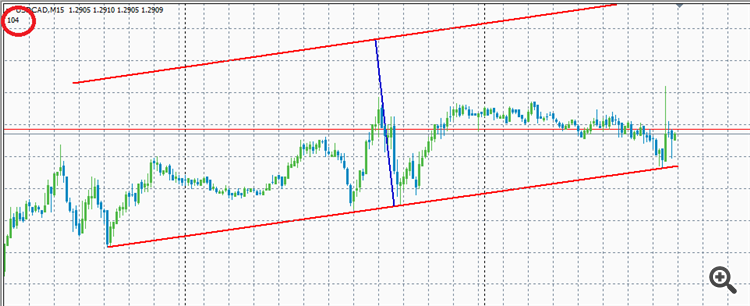
J'ai vérifié sur les captures d'écran des lignes à différentes échelles - comme vous pouvez le voir, la distance entre elles ne change pas.
Le problème dans votre cas est que dans l'espace prix/seconde, la distance entre les points n'est pas définie. Par conséquent, la distance la plus courte ne peut être trouvée.
Cela est dû au fait que les dimensions des axes sont différentes. Donc vous devez soit :
- Choisissez un facteur X entre le prix et le temps, alors la distance sera en unités la racine carrée de ( prix x seconde x X ).
- compter la distance le long d'un axe ;
La distance verticale est pratiquement inchangée avec l'horizon temporel du graphique (uniquement parce qu'il y a des barres incomplètes et des barres de week-end).
La distance horizontale ne change pas du tout.
Mais lorsqu'on mesure la distance sur un axe, elle peut être infinie, ce qui n'a aucun sens.
Pouvez-vous me dire comment calculer la distance entre deux lignes parallèles en tenant compte de l'échelle du graphique (pour que l'échelle ne soit pas affectée) ?
Voici un exemple :
La ligne rouge est la distance entre deux lignes parallèles - comment pouvez-vous la calculer ?
Comment calculer la distance entre deux lignes parallèles en tenant compte de l'échelle du graphique (de manière à ce que l'échelle ne soit pas affectée) ?
Voici un exemple :
La ligne rouge représente la distance entre deux lignes parallèles - comment calculer ?
C'est élémentaire, Watson...
Si vous voulez transposer un système bidimensionnelPrix X Temps dans le plan Prix X Prix, vous devez introduire une nouvelle caractéristique, qui s'appelle plus logiquement la vitesse de variation du prix V.
Et il est pratique de la mesurer en unités par seconde.
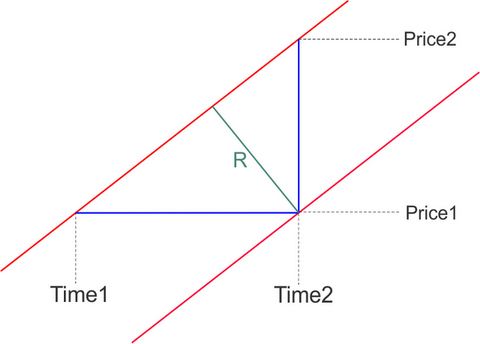
Et V = tangente de l'angle de votre ligne dans un système directement proportionnel à celui-ci :
- 1 pixel verticalement = 1 _Point
- 1 pixel horizontalement = 1 seconde (la barre des minutes fait 60 pixels de large sur votre écran)
Ensuite, la distance de deux lignes parallèles peut être calculée de deux façons :
double V=(Price2-Price1)/(Time2-Time1); ulong DeltaTime = TimeLine2-TimeLine1; // double DeltaPrice = PriceLine2- PriceLine1; double R=DeltaTime*V/sqrt(1+V*V) ; // double R=V/(DeltaPrice*sqrt(1+V*V)) ; // где // точки (Price1,Time1) и (Price2,Time2) это две любые точки лежащие на одной из параллельных линий, Time измеряется в секундах // TimeLine1 и TimeLine2 - время первой и второй линии при фиксированной цене (пересечение с горизонтальной линией) // PriceLine1 и PriceLine2- цена первой и второй линии при фиксированном времени (пересечение с вертикальной линией) // DeltaPrice - расстояние между линиями в пунктах по вертикали // DeltaTime - расстояние между линиями в секундах по горизонтали // R - искомое кратчайшее расстояние между двумя параллельными линиями, скорость измерения цены которых равна V пунктов в секунду
Il est clair que cette perpendiculaire ne ressemblera pas à une perpendiculaire dans un système dont les proportions sont différentes de celles du système ci-dessus.
C'est élémentaire, Watson...
Pour faire passer un système bidimensionnelPrix X Temps dans le plan Prix X Prix, il est nécessaire d'introduire une nouvelle caractéristique, qui s'appelle plus logiquement la vitesse de variation des prix V.
Et il est pratique de la mesurer en unités par seconde.
Et V = tangente de l'angle de votre ligne dans un système directement proportionnel à celui-ci :
- 1 pixel verticalement = 1 _Point
- 1 pixel horizontalement = 1 seconde (la barre des minutes fait 60 pixels de large sur votre écran)
La distance entre deux lignes parallèles peut alors être calculée de deux façons :
Il est clair que cette perpendiculaire n'apparaîtra pas comme une perpendiculaire dans un système dont les proportions sont différentes de celles du système précité
Nous pouvons simplifier cela car il existe un cas où Temps1=Temps1 et Temps2=Temps2.
Ensuite :
double V=(Price2-Price1)/(Time2-Time1); double R=(Price2-Price1)/sqrt(1+V*V) ;
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
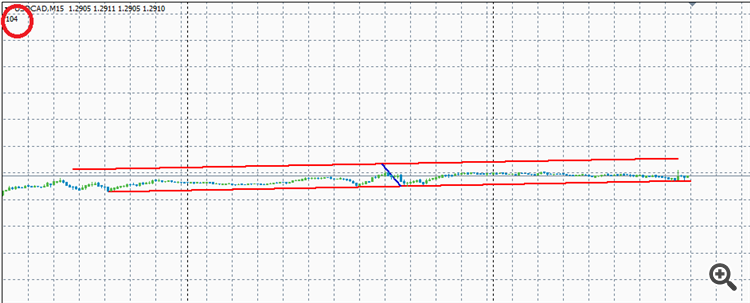
Pouvez-vous me dire comment calculer la distance entre deux lignes parallèles en tenant compte de l'échelle du graphique (pour que l'échelle ne soit pas affectée) ?
Voici un exemple :
La ligne rouge est la distance entre deux lignes parallèles - comment pouvez-vous la calculer ?