Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Merci pour le lien, je me suis laissé emporter en cherchant des idées connexes. Je ne pense pas que vous ayez besoin d'aborder la question comme cela, du point de vue des fonctions R. Approche avec des moyens conventionnels :
Directement à partir de l'équation d'un cercle de rayon R avec des coordonnées centrales Xc, Yc, en ignorant la perte de sens des unités (nombre, parcours, distance)
R^2 = (X-Xc)^2 + (Y-Yc)^2
on fait une fonction de l'incohérence au point avec le numéro i (Xi = i). C'est la différence entre la distance du point (Xi, Yi) au centre Xc, Yc et le rayon R :
Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0,5 - R.
Les carrés de Di et s'additionnent pour obtenir la fonction cible à minimiser. Il y a trois paramètres à faire varier : R, Xc, Yc. Les points les plus éloignés (premier et dernier) ont moins d'influence que les points intermédiaires (non adjacents), je pense qu'il est préférable de multiplier le Di^2 correspondant par deux. Et pour vos besoins d'ajustement en mettant l'accent sur les derniers points, vous pouvez également jouer avec les poids de plusieurs derniers points en créant une colonne supplémentaire pour les poids.
S'il n'est pas droit, il faudra tenir compte des unités de mesure. Pour que l'influence de X et Y soit presque égale dans le calcul de la distance (et que R soit affecté par les deux), il est nécessaire de prendre non pas i nombre comme X, mais le même nombre multiplié par l'échelle d'alignement, de sorte que les plages X et Y soient de taille proche.
P.S. Il s'avère que sernam.ru s'est très intelligemment débarrassé des accusations de violation des droits d'auteur en publiant les textes des livres uniquement en partie et sans spécifier les données de sortie, en particulier les titres des livres. Il est possible de trouver sur sernam.ru des textes qui ne se trouvent nulle part ailleurs sur Internet.
J'ai compris que je dois minimiser en utilisant Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R.
Il faudra ensuite tracer le cercle trouvé par jeux.
l'équation sera.
y=(R^2-(X-Xc)^2)^0.5+Yc
Donc, ne perdez pas votre temps avec cette direction. Bien que, vous pouvez construire un indicateur basé sur un arc, plutôt qu'une ligne droite, comme le mashka. peut-être cela fonctionnera-t-il mieux que le sma.
c'est la formule que j'ai prise.
l'équation générale de l'arc :
(x - L)^2+ (y + (R - H))^2 = R^2
y = sqrt(R^2 - (x - L)^2) - (R - H) , où la formule pour R est dans la figure.
Mais il ne convient que pour le plan positif. Pour l'expérience, j'ai pris un "canal de prix en arc" qui se trouve dans le plan positif.
peut-être que c'est juste un joli nom choisi...
RRR5:
...
Mais cela ne convient que pour le plan positif. Pour l'expérience, j'ai pris un "canal de prix sur un arc", qui se trouve dans le plan positif.
Qu'est-ce qu'un "plan positif" ?
Qu'est-ce que le "plan positif" ?
mais pas dans cet arc.
Eh bien, pour un arc comme celui-ci, ça va marcher.
mais pas pour celui-là.
RRR5, vous faites des dessins rapidement. Avec quoi, je me le demande ?
J'ai lu ici des articles sur les polynômes, l'ANC, les diverses méthodes d'approximation, les capacités de prévision, etc ...
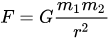
Certains croient aux prédictions, d'autres non.
Mais ce que j'espérais trouver, je ne l'ai jamais vu.
Pour tenter d'expliquer ce que je veux dire, je vais recourir à une analogie avec la gravité dans l'univers.
Voici un aperçu du gif animé que j'ai enregistré.
Répondez à la question par vous-même. Est-il possible de prédire la trajectoire de chaque objet ?
Bien sûr, vous pouvez.
Mais seulement si vous connaissez des informations sur chaque objet à ce moment-là : sa masse, sa position actuelle et la direction de son mouvement, l'heure de son apparition et l'heure de sa disparition.
Et puis, c'est une question de mathématiques et de calculs, utilisant essentiellement une seule formule (pour une variante de la mécanique classique pour les vitesses éloignées de la vitesse de la lumière) :
le programme lui-même est un brouilleur de gravité juste ici. Vous pouvez jouer avec.
Il est également nécessaire de comprendre que même notre planète ne se déplace pas en cercle fermé, mais en fait une onde sinusoïdale tridimensionnelle (spirale).
Cette vidéo le démontre clairement :
Et si nous n'avons pas d'informations sur tous les objets ?
Peut-on prédire la trajectoire en ne connaissant que la trajectoire elle-même dans le passé ?
C'est là que le plaisir commence.
Si quelqu'un dit que ce n'est pas possible, la réponse est fausse. Une réponse affirmative serait également erronée.
La solution à ce problème ne sera que probabiliste.
Le problème doit être résolu dans le sens inverse. En fonction de la trajectoire passée, nous devons d'abord calculer les trajectoires probabilistes des principaux "amas" d'objets et leur masse. Pour ensuite prédire des modèles probabilistes de trajectoires possibles.
C'est à cela que sert la tâche de base de l'IA : la reconnaissance des formes.
C'est, si je comprends bien, ce dont parlait Maxime Dmitrievsky.
Il y a environ six ans, j'ai publié mes premiers développements dans ce domaine dans le KB: https://www.mql5.com/ru/code/10882. J'ai juste utilisé un polynôme de degré 1 (Régression linéaire) pour la reconnaissance des canaux là. Par la suite, j'ai considérablement progressé dans ce domaine. Mais je ne publie rien et ne le ferai pas pour des raisons évidentes. Je ne donne que des indices pour les esprits curieux.
Trouver des canaux linéaires revient essentiellement à trouver les centres de ces masses gravitationnelles.
Il y a généralement 5 à 10 centres (canaux) de ce type dans un instrument (symbole). Pour la prédiction du prix, tous ces éléments doivent être pris en compte simultanément. Dans ce cas seulement, la précision de la prédiction à la hausse ou à la baisse sera bien supérieure à 50 %.
Mais tout le monde essaie de trouver un ensemble spécial de chiffres et croit naïvement qu'ils permettront de prédire l'avenir.
Le problème est que cet "ensemble de nombres" est vivant, dynamique, il change constamment, de même que la position des centres de masse locaux d'un ensemble d'objets, par analogie avec une gravitation matérielle, change. Et le problème se réduit à trouver la loi de changement de cet "ensemble de nombres" et même à trouver la loi de changement de la loi elle-même :)))
Idéalement, cet "ensemble de chiffres" devrait être recalculé à chaque tic. C'est exactement la raison pour laquelle j'ai dit plus d'une fois que ce que beaucoup appellent l'optimisation, la recherche d'un "ensemble de chiffres" particulier, est un trivial bricolage de données historiques.
Je pense que l'analogie avec la gravité est très pertinente. Sur le marché, la gravité est créée par l'argent. Certains y vont avec 100 dollars, d'autres avec quelques milliards. Les mêmes lois de la gravité s'appliquent ici, et même la même formule que j'ai donnée ci-dessus. La force d'attraction est inversement proportionnelle au carré de la distance et directement proportionnelle aux masses. Par conséquent, une régression polynomiale de degré 2 (parabole) est l'outil le plus approprié. Bien qu'il serait plus logique d'utiliser une hyperbole, car c'est selon les lois de l'hyperbole que deux corps gravitationnels interagissent. Mais le fait est que la parabole est beaucoup plus pratique pour les calculs, et que la parabole et l'hyperbole sont très similaires l'une à l'autre dans l'intervalle le plus important.
Vous pouvez le voir clairement ici. La ligne rouge est la parabole et la ligne bleue est l'hyperbole.
La principale différence entre la gravité de l'argent et celle des corps célestes est que l'argent peut apparaître et disparaître soudainement, créant ainsi de puissantes fluctuations gravitationnelles. Mais pour calculer cet événement, et il existe une telle chose qu'une panne de canal.
La solution à ce problème ne sera que probabiliste.
Le problème doit être résolu à l'envers. A partir de la trajectoire passée, il faut d'abord calculer les trajectoires probabilistes des principaux "clusters" d'objets et leur masse. Pour ensuite prédire des modèles probabilistes de trajectoires possibles.
Je crains que la "solution probabiliste" ici ne soit l'ensemble des trajectoires dans un espace donné - et quelle est la valeur de cette solution ?
Ce serait comme affirmer "avec une forte probabilité" que l'eurodollar ne sera pas négatif cette année, pas plus de 100. Remarquez que la probabilité de cette affirmation est proche de 100%. Mais une telle "prédiction" vous serait-elle d'une grande utilité ?
En théorie des probabilités, il est prouvé que lorsque l'état d'un objet est influencé par de nombreuses forces indépendantes, la probabilité de cet état commence à obéir à la loi gaussienne. Toutefois, l'évolution et la valeur des prix n'obéissent pas à cette distribution, pour la simple raison que les entrées et les sorties des participants au marché sont dépendantes.
RRR5:
понял, что минимизировать нужно по формуле Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R.
...
Pour l'expérience, j'ai pris un "canal de prix sur un arc", qui se trouve dans le plan positif.
Je ne comprends toujours pas pourquoi tu n'aimes pas le MNC. Il est possible de tracer n'importe laquelle des courbes en question.
J'aime travailler sur de petites TF, mais je n'aime pas ces snafus.
Comment les prévoir ?