Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Если приращения случайны, то цена - это random walk, она имеет нормальное распределения, и заработать на ней гарантированно нельзя.
Однако надо оговорить природу приращения, сказать просто "случайная" - не сказать ничего. В жизни всё случайно. У автобуса есть расписание, но время его прибытия величина случайная. Случайные приращения цены могут быть коррелированы с фазами луны, например, это не делает их неслучайными.
Чтобы получить random walk приращения должны быть iid независимыми и одинаково распределёнными.
C'est là le problème : l'augmentation des prix n'est pas normalement distribuée. Sinon, il serait garanti de gagner de l'argent avec.
В том то и дело, что приращение цены не нормально распределено. Иначе заработать на нем было бы гарантированно можно.
par rapport à quoi sont les incréments anormaux ?
В том то и дело, что приращение цены не нормально распределено. Иначе заработать на нем было бы гарантированно можно.
On peut supposer que l'augmentation du prix est normalement distribuée, ce qui est assez proche de la réalité, mais cela ne sert à rien si elle est iid . L'augmentation du prix peut être considérée comme distribuée en t avec des degrés de liberté de 4 ou 5. Cela est beaucoup plus proche de la réalité que de supposer que les incréments sont normaux.
Le processus résultant sera une marche aléatoire. Il est garanti qu'il est normalement distribué, quelle que soit la distribution des incréments, mais la normalité ne sert à rien - vous ne pouvez pas gagner de l'argent sur une marche aléatoire. Les incréments de prix peuvent être considérés comme stationnaires, mais ils ne peuvent pas être échangés. Vous pouvez négocier le prix, et c'est une marche aléatoire, un processus non stationnaire. Du moins dans le contexte de ce sujet.
Приращение цены можно считать нормально распределённым - это достаточно близко к реальности, однако это ничего не даст, если оно iid . Можно считать приращение цены t-распределённым со степенью свободы 4 или 5. Это гораздо ближе к реальности, чем допущение о нормальности приращений.
Результирующий процесс будет random walk. Вот он-то вообще гарантированно нормально распределённый, независимо от распределения приращений, но от той нормальности никакого прока - нельзя заработать на случайном блуждании. Приращение цены можно считать стационарными, но их нельзя торговать. Торговать можно цену, а она random walk, процесс нестационарный. По крайней мере в контексте данного топика.
Puis-je argumenter un peu pour faire avancer la discussion ? Je ne suis pas très sûr de ce que je veux dire pour le moment. Surtout maintenant qu'il est très tard. Mais quand même... Si les incréments d'une certaine quantité sont normalement distribués, cela signifie que cette quantité est bornée. (Est-ce que je me trompe ?).
Sauf erreur de l'affirmation précédente, il existe une valeur maximale et une valeur minimale dans l'ensemble des valeurs d'une quantité. De même, plus la valeur d'une valeur est proche du maximum ou du minimum, plus il est probable qu'elle évolue vers la moyenne. C'est la loi qui peut être utilisée.
p.s. Ne pensez pas que je vous attaque. Je veux juste avoir une conversation avec une personne intelligente.
Можно я для поддержания дискуссии немножко поспорю? Я сейчас сам не очень уверен в том, что хочу сказать. Тем более уже очень поздно. Но все-таки... Если приращения какой-то величины нормально распределены, то это значит, что эта величина ограничена. (Ошибаюсь?)
Если не ошибся в предыдущем утверждении, то во множестве значений величины есть максимумальное и минимальное. Кроме того, чем ближе значение величины к максимальному или минимальному, тем больше вероятность его изменения в сторону среднего. Вот это и есть закон, который можно использовать.
п.с. Не подумайте, что я нападаю. Просто хочу поговорить с умным человеком.
N'avez-vous pas entendu parler du théorème de l'arc-en-ciel et de l'erreur du joueur ?
Je n'ai pas demandé la relativité de la déviation pour rien.
S'il revient - une chanson.
MA(x période) est une autre chanson...
Si vous utilisez TrueDMA au lieu de MA - une cacaphonie complètement différente s'abattra sur vous.
;)
Où avez-vous trouvé l'anomalie ?
Ne demandez à personne, ils ne disent pas un mot.
Il y a un sujet - il montre le contraire.
Yo mon...
:)
Можно я для поддержания дискуссии немножко поспорю? Я сейчас сам не очень уверен в том, что хочу сказать. Тем более уже очень поздно. Но все-таки... Если приращения какой-то величины нормально распределены, то это значит, что эта величина ограничена. (Ошибаюсь?)
Если не ошибся в предыдущем утверждении, то во множестве значений величины есть максимумальное и минимальное. Кроме того, чем ближе значение величины к максимальному или минимальному, тем больше вероятность его изменения в сторону среднего. Вот это и есть закон, который можно использовать.
п.с. Не подумайте, что я нападаю. Просто хочу поговорить с умным человеком.
Vous avez définitivement tort. La nature de la distribution ne dit rien sur la limitation de la valeur. Il y a probablement quelques exceptions, mais en général, c'est le cas. Les limites sont imposées par les paramètres de la distribution. Par exemple : la prévalence normalement distribuée est ~N(0,1). C'est un processus stationnaire, il a des limites de magnitude, il n'atteindra presque jamais 4 ou -4.
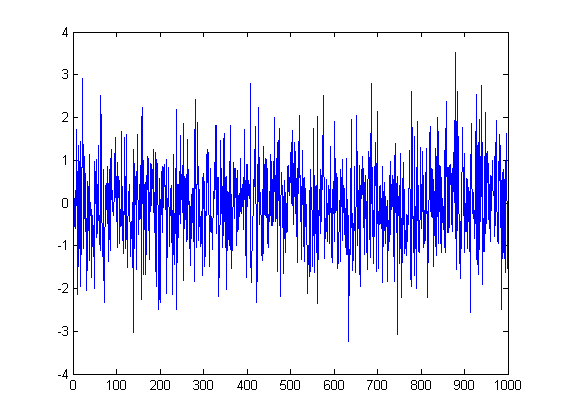
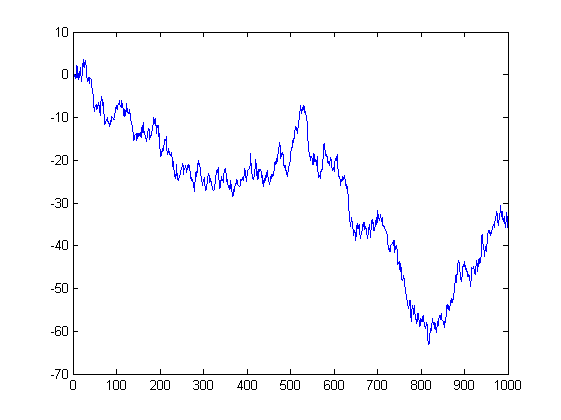

Et voici le prix qui résulte de ces incréments. C'est une marche aléatoire. Elle aussi a une distribution normale ~N(0,sigma^2), mais son paramètre de variance n'est pas une constante, mais augmente avec le temps, c'est-à-dire le nombre d'incréments. Naturellement, ce processus n'a pas de limite de taille et visitera tous les points avec la même probabilité. C'est la base du problème de la faillite du joueur - si vous jouez assez longtemps dans un jeu parfaitement équitable (50:50), vous perdrez quand même, car tôt ou tard, cette courbe vous mènera plus bas que votre argent.
Et voici 1 000 marches aléatoires, vous pouvez évidemment voir la cloche de la distribution normale.
Mais ce que vous dites à propos du retour à la moyenne est une autre histoire, c'est un processus de retour à la moyenne - autorégressif (AR).
x(i) = a * x(i-1) + e(i). La transformation e(i) est ~N(0,1), a < 1.
Si vous avez trouvé un processus de retour à la moyenne négociable, il ne vous reste plus qu'à transporter des paniers de choux. Naturellement, cela dépend des paramètres - le taux de retour à la moyenne (a) - mais dans tous les cas, c'est cool.
А вот 1000 случайных блужданий, очевидно виден колокол нормального распределения.
vous devez allumer les fréquences des coups.
--
le double King(log) Bell en expansion.
;)
не всякий увидит.
Vous avez un histogramme et un diagramme de probabilité pour le 1000ème échantillon.


Bien que, puisque les incréments étaient normaux, la somme des distributions normales est une distribution normale. Vous n'avez même pas besoin de vérifier quoi que ce soit.
На тебе гистограмму и пробабилити плот для 1000-го отсчёта.
Хотя исходя из того, что приращения были нормальные, сумма нормальных распределений есть нормальное распределение. Тут ничего даже и проверять-то не надо.
Sens !
Bon travail (ou plutôt - et visuellement utile ;).