Discusión sobre el artículo "Algoritmos de optimización de la población: Algoritmo de optimización de la dinámica espiral (Spiral Dynamics Optimization, SDO)"
Me gustaría consultar con la comunidad.
Otros algoritmos asombrosos están esperando su turno, la tabla de comparación se hace demasiado grande para una visualización y análisis convenientes, pienso excluir a los más débiles de la tabla, pero por otro lado no me gustaría perderlos de vista.
Además, tal vez podría hacer alguna otra visualización.
En general, estaré encantado de escuchar sus comentarios y sugerencias.
Espero que mis artículos sirvan de fuente de ideas e inspiración para los operadores, ayuden a mirar las cosas ordinarias con una mirada nueva y fresca, así como ayuden a elegir las herramientas adecuadas en la búsqueda de interrelaciones complejas, ayuden a conseguir objetivos y nuevos éxitos impresionantes.
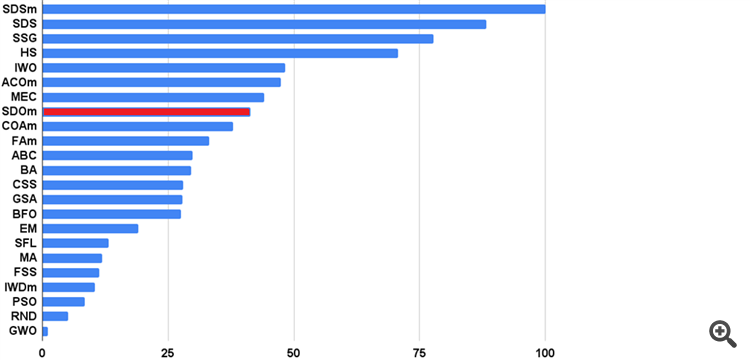
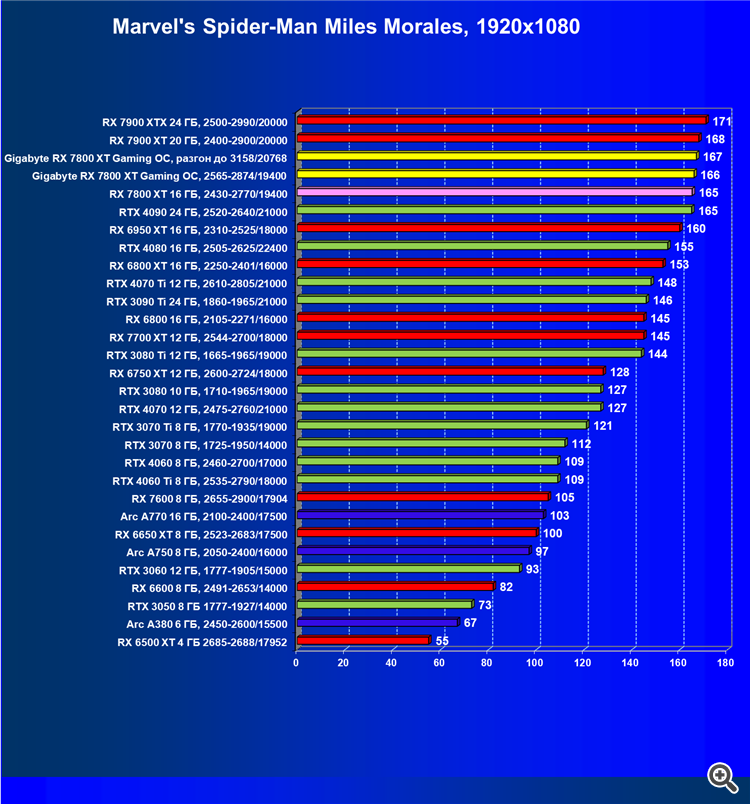
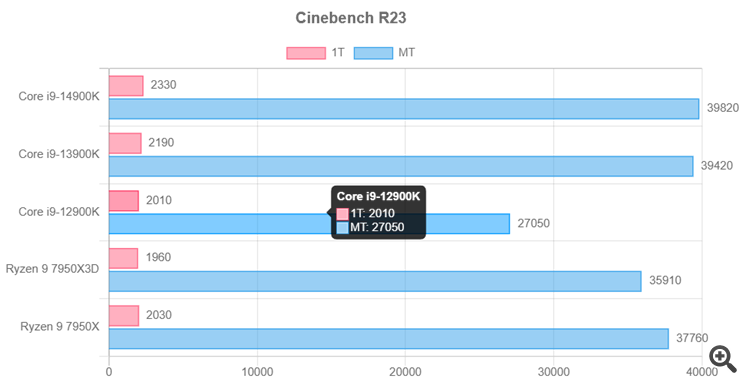
Mira los sitios donde se han elaborado las formas más exitosas de visualizar datos comparativos a lo largo de los años.
Mira los sitios donde se han elaborado las opciones más exitosas para visualizar datos comparativos a lo largo de los años.
Sí, un gráfico de barras (histograma) es una buena forma de mostrar lo que se compara, no hay problema con eso.
Me refería a que quizá valga la pena dar además del histograma general también por separado para cada prueba (y son 9). Una tabla coloreada está bien y permite identificar claramente las especificidades de cada algo, pero no da una idea de hasta qué punto difieren de una disciplina a otra.
Y, aunque sólo cito algoritmos honestos (aunque algunos de ellos no lo fueran, son reelaborados), todavía puede haber algunos que puedan utilizar la repetibilidad en las funciones de prueba como "arma".
Hace poco me topé con un algoritmo de este tipo, los autores utilizaban la búsqueda del mínimo en la función Rastrigin, pero es absolutamente seguro que el glob min está en [0,0] (justo en el centro del área de definición de la función), con la consiguiente "frialdad" imaginaria de dicho algoritmo.
Por eso estoy trabajando en la idea de revisar la metodología de las pruebas para deshacerme de la duplicación de funciones bidimensionales en un espacio multidimensional y, al mismo tiempo, preservar la posibilidad de visualizar el proceso de pruebas, y esta es una cuestión muy difícil como puede parecer a primera vista.
Andrei, ¿de dónde sacas esto
Esa es una pregunta en tu mente.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Artículo publicado Algoritmos de optimización de la población: Algoritmo de optimización de la dinámica espiral (Spiral Dynamics Optimization, SDO):
Este artículo presenta un algoritmo de optimización basado en los patrones de las trayectorias en espiral en la naturaleza, como las conchas de los moluscos: el algoritmo de optimización de la dinámica espiral o SDO. El algoritmo propuesto ha sido repensado y modificado a fondo por el autor: en el artículo analizaremos por qué estos cambios han sido necesarios.
El algoritmo de optimización de la dinámica espiral (SDO) es uno de los algoritmos físicos más simples propuesto por Tamura y Yasuda en 2011 y desarrollado utilizando el fenómeno de la espiral logarítmica en la naturaleza. El algoritmo es simple y tiene pocos parámetros de control. Además, tiene una alta velocidad de cálculo, capacidad de búsqueda local, diversificación en la fase inicial e intensificación en la fase posterior.
En la naturaleza existen muchas espirales, como galaxias, auroras, cuernos de animales, tornados, conchas marinas, caracoles, amonites, colas de camaleón y caballitos de mar. Las espirales también pueden verse en el arte antiguo creado por la humanidad en los albores de su existencia. A lo largo de los años, varios investigadores se han esforzado por comprender las secuencias y complejidades de las espirales y desarrollar ecuaciones y algoritmos para estas. Cabe destacar que un fenómeno espiral que se da con frecuencia en la naturaleza es la espiral logarítmica, que puede observarse en galaxias y ciclones tropicales. Los procesos discretos de generación de espirales se implementaron como un comportamiento de búsqueda eficiente en metaheurísticas, lo cual inspiró el desarrollo de un algoritmo de optimización de dinámica espiral.
Los ornamentos denominados secuencias espirales visibles que se encuentran en la naturaleza constituyen plantas, árboles, olas y muchas otras formas. Los patrones visuales de la naturaleza pueden modelarse usando la teoría del caos, los fractales, las espirales y otros conceptos matemáticos. En algunos patrones naturales, las espirales y los fractales se encuentran estrechamente relacionados. Por ejemplo, la espiral de Fibonacci es una variante de la espiral logarítmica basada en la proporción áurea y los números de Fibonacci. Al ser logarítmica, la curva posee el mismo aspecto a todas las escalas, por lo que también puede considerarse un fractal.
Autor: Andrey Dik